Codeforces 716 E Digit Tree

E. Digit Tree

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

ZS the Coder has a large tree. It can be represented as an undirected connected graph of n vertices numbered from 0 to n - 1 and n - 1edges between them. There is a single nonzero digit written on each edge.

One day, ZS the Coder was bored and decided to investigate some properties of the tree. He chose a positive integer M, which is coprime to 10, i.e. .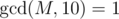

ZS consider an ordered pair of distinct vertices (u, v) interesting when if he would follow the shortest path from vertex u to vertex v and write down all the digits he encounters on his path in the same order, he will get a decimal representaion of an integer divisible by M.

Formally, ZS consider an ordered pair of distinct vertices (u, v) interesting if the following states true:

• Let a1 = u, a2, ..., ak = v be the sequence of vertices on the shortest path from u to v in the order of encountering them;
• Let di (1 ≤ i < k) be the digit written on the edge between vertices ai and ai + 1;
• The integer 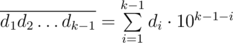 is divisible by M.

Help ZS the Coder find the number of interesting pairs!

Input

The first line of the input contains two integers, n and M (2 ≤ n ≤ 100 000, 1 ≤ M ≤ 109, 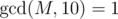) — the number of vertices and the number ZS has chosen respectively.

The next n - 1 lines contain three integers each. i-th of them contains ui, vi and wi, denoting an edge between vertices ui and vi with digit wi written on it (0 ≤ ui, vi < n,  1 ≤ wi ≤ 9).

Output

Print a single integer — the number of interesting (by ZS the Coder's consideration) pairs.

Examples

input

6 7
0 1 2
4 2 4
2 0 1
3 0 9
2 5 7

output

7

input

5 11
1 2 3
2 0 3
3 0 3
4 3 3

output

8

虽然不是很难想但是差点调死我hhhhh
首先这道题和常规点分治不太一样的地方是，普通的点分治一般是无向路径，我们往往不用考虑起点和终点而是直接考虑路径的两个端点就行了。
但是本题是有向路径，不同的方向意味着不同的数字。

而且本题还要一个坑爹的地方是知道终点好找起点，但是知道起点不好找终点。。。。。
当然有两种解决方法：
1.对于当前的重心选任意两条路径统计一遍，再把在同一颗子树内的减掉。
2.考虑到起点要么比终点先被扫到，要么晚被扫到，那么我们就正反两遍常规的calc，这样还不用去重。

我就是用的第二种方法。。。

然后千万别忘了起点或终点是重心的情况，，，，但这样不太可能，因为这样例都过不了hhhh

对于点分的每层我们用map记录一下起点的情况，然后用扫到的终点更新答案。
至于怎么更新答案，就是一个式子，推一下就好了也不难hhhh

当然如果你把向下和向上的路径写反了(就像一开始的我)是要调很久的hhhh，因为样例里并没有长度>=3的路径。

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<map>
#include<algorithm>
#define ll long long
#define maxn 100005
using namespace std;
map<int,int> mmp;
int ci[maxn],n,m,num=,b[maxn];
int to[maxn*],ne[maxn*];
int hd[maxn],sz,minn,root;
int d[maxn],tot,ni[maxn];
int siz[maxn],val[maxn*];
ll ans;
bool done[maxn];

inline void add(int uu,int vv,int ww){
    to[++num]=vv,ne[num]=hd[uu],hd[uu]=num,val[num]=ww;
}

void froot(int x,int fa){
    siz[x]=;
    int bal=;
    for(int i=hd[x];i;i=ne[i]) if(!done[to[i]]&&to[i]!=fa){
        froot(to[i],x);
        siz[x]+=siz[to[i]];
        bal=max(bal,siz[to[i]]);
    }

    bal=max(bal,sz-siz[x]);
    if(bal<minn) minn=bal,root=x;
}

int fsiz(int x,int fa){
    int an=;
    for(int i=hd[x];i;i=ne[i]) if(!done[to[i]]&&to[i]!=fa){
        an+=fsiz(to[i],x);
    }
    return an;
}

void dfs(int x,int fa,int dep,int dx,int dy,int tmp){
    int tox=(ll)(m-dy)*(ll)ni[dep]%m;
    if(mmp.count(tox)) ans+=(ll)mmp[tox];
    if(tmp){
        if(!dx) ans++;
        if(!dy) ans++;
    }

    d[++tot]=dx;

    for(int i=hd[x];i;i=ne[i]) if(!done[to[i]]&&to[i]!=fa){
        dfs(to[i],x,dep+,((ll)dx+(ll)val[i]*(ll)ci[dep])%m,((ll)dy*10ll+(ll)val[i])%m,tmp);
    }
}

inline void calc(int pos,int va,int tmp){
    int pre=tot+;
    dfs(pos,pos,,va,va,tmp);
    for(;pre<=tot;pre++){
        if(!mmp.count(d[pre])) mmp[d[pre]]=;
        else mmp[d[pre]]++;
    }
}

inline void work(int x,int trsiz){
    sz=trsiz,minn=<<;
    froot(x,x);
    done[root]=;

    int len=;
    for(int i=hd[root];i;i=ne[i]) if(!done[to[i]]){
        b[++len]=i;
        calc(to[i],val[i],);
    }

    mmp.clear(),tot=;

    for(;len;len--){
        calc(to[b[len]],val[b[len]],);
    }

    mmp.clear(),tot=;
    for(int i=hd[root];i;i=ne[i]) if(!done[to[i]]){
        work(to[i],fsiz(to[i],to[i]));
    }
}

void gcd(int aa,int bb,ll &xx,ll &yy){
    if(!bb){
        xx=,yy=;
        return;
    }

    gcd(bb,aa%bb,yy,xx);
    yy-=xx*(ll)(aa/bb);
}

inline int get_ni(int x){
    ll xx,yy;
    gcd(x,m,xx,yy);
    return (xx+m)%m;
}

int main(){
    scanf("%d%d",&n,&m);
    ci[]=ni[]=;
    for(int i=;i<=n;i++) ci[i]=(ll)ci[i-]*10ll%m,ni[i]=get_ni(ci[i]);
    //printf("%d %d %d\n",i,ci[i],ni[i]);

    int uu,vv,ww;
    for(int i=;i<n;i++){
        scanf("%d%d%d",&uu,&vv,&ww),uu++,vv++;
        ww%=m;
        add(uu,vv,ww),add(vv,uu,ww);
    }

    work(,n);

    cout<<ans<<endl;
    return ;
}