《机器学习基石》第一周 —— When Can Machine Learn?

（注：由于之前进行了吴恩达机器学习课程的学习，其中有部分内容与机器学习基石的内容重叠，所以以下该系列的笔记只记录新的知识）

《机器学习基石》课程围绕着下面这四个问题而展开：

主要内容：

一、什么时候适合用机器学习？

二、该课程所采用的一套符号表示

三、机器学习的流程

四、感知机算法

五、学习的类型

六、机器学习的无效性

七、机器学习的可行性（在无效性的前提下加一些条件限制）

一、什么时候适合用机器学习？

对于第一点：我们学习的对象必须要存在某些显式的或者潜在的规律，否则，如果学习对象都毫无规律，那么学习到的所谓的知识（经验）也就站不住脚了。

对于第二点：这些问题难以使用某些算法或者公式明确地算出结果，假如可以，那么我们就只需要学习数学和算法就足以解决问题，又何须机器学习呢？所以机器学习就是可以用来解决这些有规律但规律又相对模糊的问题。

对于第三点：只有依靠以往大量的经历所得到的经验，才是可靠的。

二、该课程所采用的一套符号表示

三、机器学习的流程

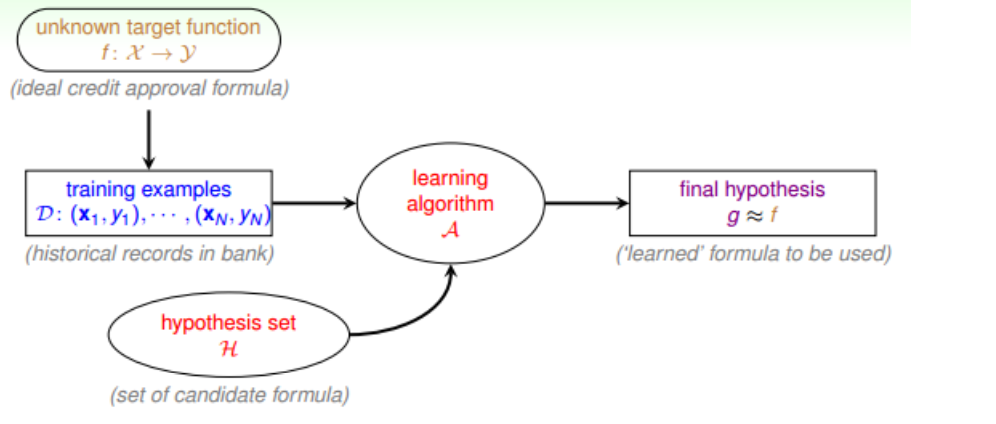
四、感知机算法

五、学习的类型

1.根据输出y的取值类型而区别，有分类、回归、结构化学习：

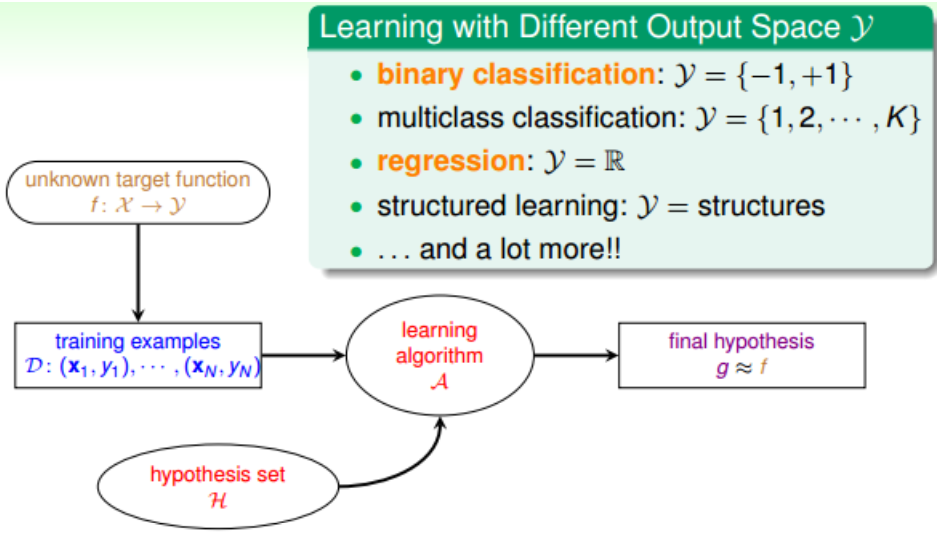
2.根据（样本）输出y的有无或者有多少而区别，有监督式学习、无监督式学习、半监督式学习、增强式学习：

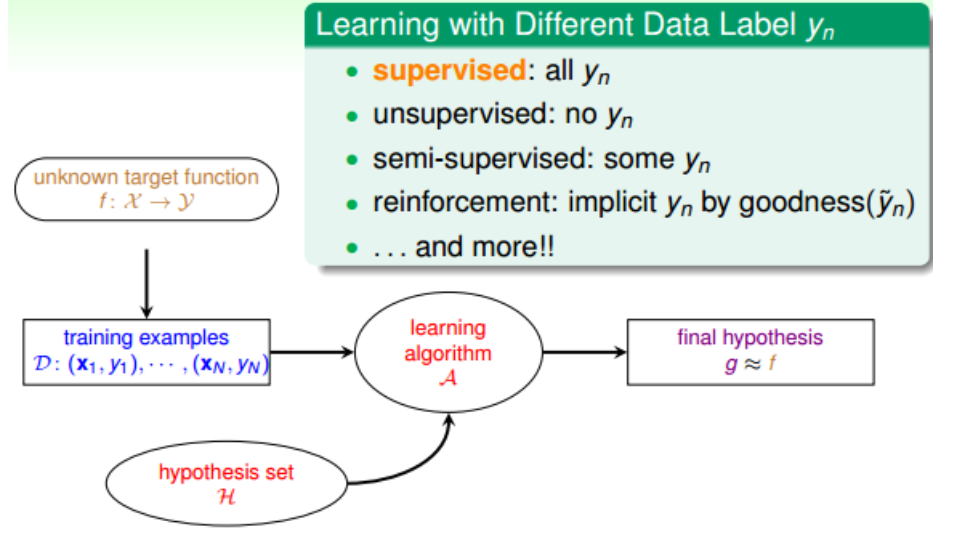
3.根据学习的协议而区别，有：batch leanring、online leanring、active learning：

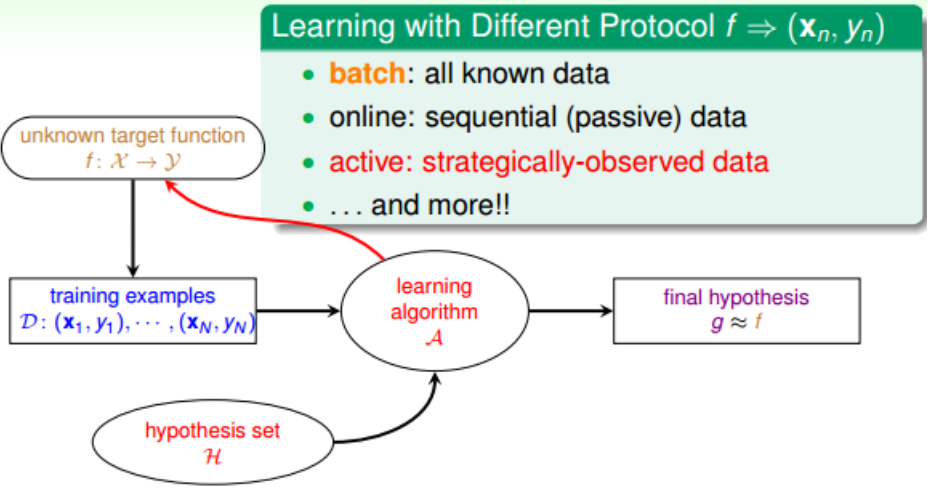
4.根据输入x的类型而区别，有：concrete features、raw features、abstract feature。

concrete features：有具体的、形象化的含义，例如身高、点击次数等这些特征。

raw features：原始的、未经过处理的特征，例如图片的像素等。

abstract feature：没有现实含义的，如资料编号或者用户ID。

5.总结：

六、机器学习的无效性

所谓机器学习的无效性，按照个人的理解，就是：单凭从给出的数据集中学习到的规律无法应用于数据集之外的数据，或者说是：每个人都学习到了不同的规律，且这些规律对于数据集都是成立的，但是对于数据集之外的数据就不成立了，这就是机器学习的不可行性。但是，假如增加一些条件限制，机器学习就可行了。其中一个很重要的条件限制就是：样本大小，也就是数据集的大小N足够大。下节详情。

七、机器学习的可行性

1.证明机器学习可行性的式子就是Hoeffding's inequality，其中u是实际上类别0的比例（假设是二分类），v是数据集（样本）类别0的比例：

当N足够大时，v就近似等于u，这就说明了从样本集中学到的规律，就近似是真实的规律，这样就能将学习到的规律应用到数据集之外的数据了。

2.对上面的结论作更严谨的推导：

设u = Ein(h)，v = Eout(h)，其中Ein(h)为h固定时h对样本预测的错误率， Eout(h)为固定时h对测试数据(或者说所有数据)预测的错误率。

所以，如果样本集的大小N足够大，那么：

注意，当Ein(h) 约等于 Eout(h)时，并不意味着h约等于f，因为Ein(h)和 Eout(h)可能很大，这样h的预测效果就非常差了。只有保证了Ein(h)很小的情况下，才能求出最接近f的h。而各种优化算法如梯度下降、最小二乘法等，就是使得Ein(h)非常小的有力工具。

3.综上，保证机器学习可行性的条件至少有两点：

1) 样本（训练集）足够大：保证了Ein(h) 约等于 Eout(h)。

2) Ein(h)足够小：保证了Eout(h)足够小，即保证了h对所有数据的预测误差足够小。