[ZJOI2009]函数 BZOJ1432

题目描述

有n 个连续函数fi (x)，其中1 ≤ i ≤ n。对于任何两个函数fi (x) 和fj (x),(i != j)，恰好存在一个x 使得fi (x) = fj (x)，并且存在无穷多的x 使得fi (x) < fj (x)。对于任何i; j; k，满足1 ≤ i < j < k ≤ n，则不存在x 使得fi (x) = fj (x) = fk (x)。

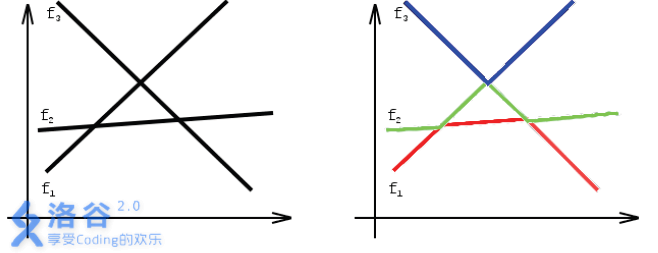
如上左图就是3 个满足条件的函数，最左边从下往上依次为f1; f2; f3。右图中红色部分是这整个函数图像的最低层，我们称它为第一层。同理绿色部分称为第二层，蓝色部分称为第三层。注意到，右图中第一层左边一段属于f1，中间属于f2，最后属于f3。而第二层左边属于f2，接下来一段属于f1，再接下来一段属于f3，最后属于f2。因此，我们称第一层分为了三段，第二层分为了四段。同理第三层只分为了两段。求满足前面条件的n 个函数，第k 层最少能由多少段组成。

输入输出格式

输入格式：

一行两个整数n; k。

输出格式：

一行一个整数，表示n 个函数第k 层最少能由多少段组成。

输入输出样例

输入样例#1：
复制

1 1

输出样例#1： 复制

1

说明

对于100% 的数据满足1 ≤ k ≤ n ≤ 100。

不太会证明。。。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstdlib>
#include<cstring>
#include<string>
#include<cmath>
#include<map>
#include<set>
#include<vector>
#include<queue>
#include<bitset>
#include<ctime>
#include<deque>
#include<stack>
#include<functional>
#include<sstream>
//#pragma GCC optimize(2)
//#include<cctype>
//#pragma GCC optimize("O3")
using namespace std;
#define maxn 700005
#define inf 0x3f3f3f3f
#define INF 9999999999
#define rdint(x) scanf("%d",&x)
#define rdllt(x) scanf("%lld",&x)
#define rdult(x) scanf("%lu",&x)
#define rdlf(x) scanf("%lf",&x)
#define rdstr(x) scanf("%s",x)
typedef long long  ll;
typedef unsigned long long ull;
typedef unsigned int U;
#define ms(x) memset((x),0,sizeof(x))
const long long int mod = 1e9 + 7;
#define Mod 1000000000
#define sq(x) (x)*(x)
#define eps 1e-3
typedef pair<int, int> pii;
#define pi acos(-1.0)
//const int N = 1005;
#define REP(i,n) for(int i=0;i<(n);i++)

inline ll rd() {
	ll x = 0;
	char c = getchar();
	bool f = false;
	while (!isdigit(c)) {
		if (c == '-') f = true;
		c = getchar();
	}
	while (isdigit(c)) {
		x = (x << 1) + (x << 3) + (c ^ 48);
		c = getchar();
	}
	return f ? -x : x;
}

ll gcd(ll a, ll b) {
	return b == 0 ? a : gcd(b, a%b);
}
ll sqr(ll x) { return x * x; }

/*ll ans;
ll exgcd(ll a, ll b, ll &x, ll &y) {
	if (!b) {
		x = 1; y = 0; return a;
	}
	ans = exgcd(b, a%b, x, y);
	ll t = x; x = y; y = t - a / b * y;
	return ans;
}
*/

ll qpow(ll a, ll b, ll c) {
	ll ans = 1;
	a = a % c;
	while (b) {
		if (b % 2)ans = ans * a%c;
		b /= 2; a = a * a%c;
	}
	return ans;
}

int main(){
	//ios::sync_with_stdio(0);
	int n, k; cin >> n >> k;
	if (n == 1)cout << 1 << endl;
	else cout << 2 * (min(k, n - k + 1)) << endl;
    return 0;
}