洛谷p2149----两个终点和两个起点，最短路最大交汇长度！！！

说实话，这题真第一次见，学到了不少有趣的东西，因吹丝汀！！

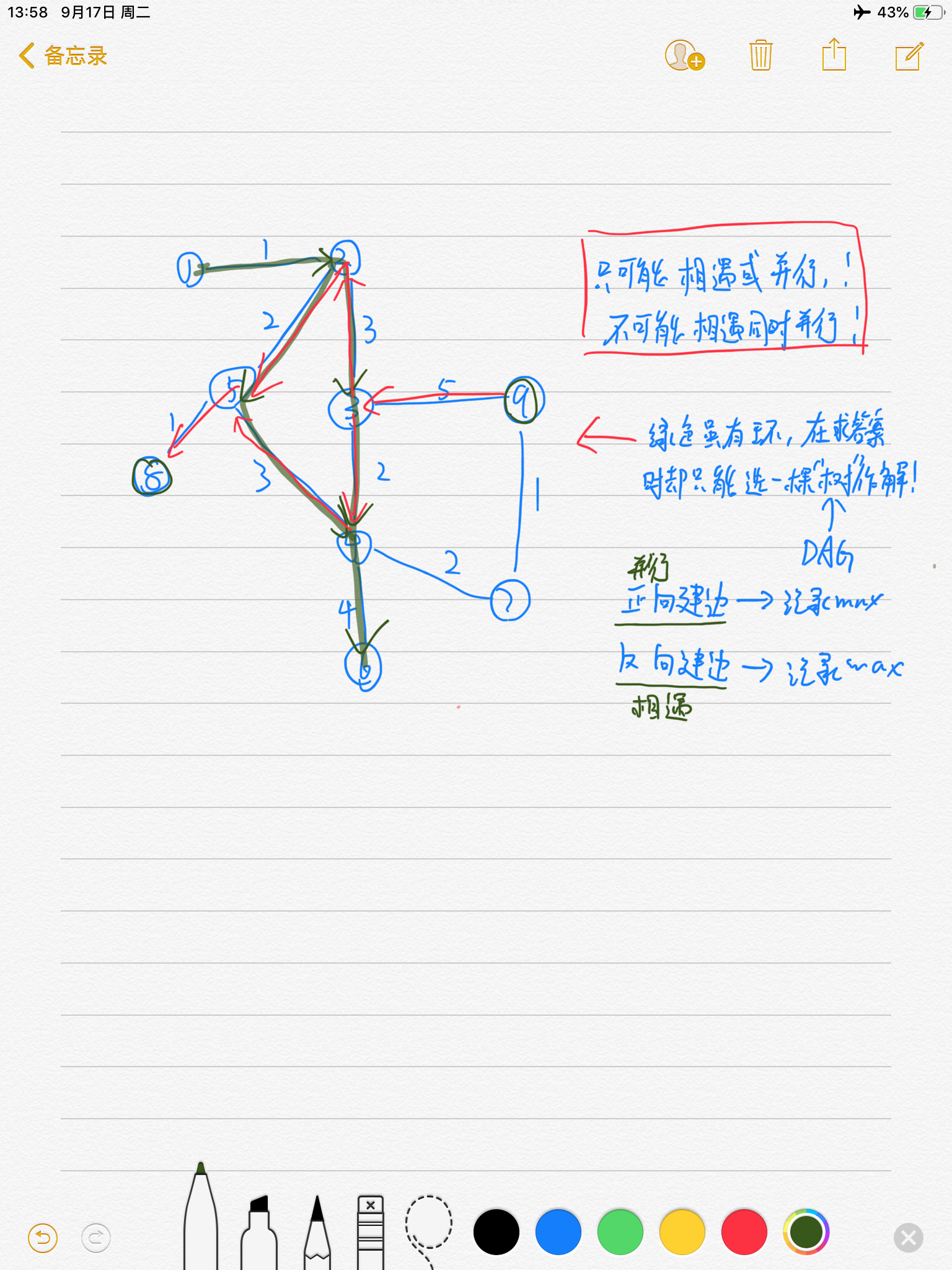
思路：因为不可能同时并行和相遇（我也不知道为啥，等我会证明了就来说说）

所以正向建边再反向建边，拓扑排序+dp求最下长路，记录下最大的就是解

高中生的OI题好难呀

#include<iostream>
#include<vector>
#include<cstring>
#include<cstdio>
#include<queue>
#include<algorithm>
#include<map>
using namespace std;
#define maxn 2000
const int mod = 10000;
map<long long, int>ins;
struct Node {
	int p;
	int len;
	Node(int a, int b) :p(a), len(b) {}
};
bool operator < (const Node a, const Node b) {
	return a.len > b.len;
}

vector<Node>G[maxn], G2[maxn];
int vis[maxn];

void insert(int be, int en, int len) {
	G[be].push_back(Node(en, len));
}
int dijstra(int be, int *dis) {
	for (int i = 1; i <= 1999; i++) dis[i] = 0x3f3f3f3f;
	memset(vis, 0, sizeof(vis));
	priority_queue<Node>que;
	que.push(Node(be, 0));
	dis[be] = 0;
	while (!que.empty()) {
		Node ans = que.top();
		que.pop();
		if (vis[ans.p] == 0) {
			vis[ans.p] = 1;
			for (int i = 0; i < G[ans.p].size(); i++) {
				int p = G[ans.p][i].p;
				if (dis[p] > dis[ans.p] + G[ans.p][i].len) {
					dis[p] = dis[ans.p] + G[ans.p][i].len;
					que.push(Node(p, dis[p]));
				}
			}
		}
	}
	return 0;
}
int de[maxn];//度数
int n, m;
int ddd[maxn];
int topu() {
	queue<int>que;
	for (int i = 1; i <= n; i++) if (de[i] == 0) que.push(i);
	while (!que.empty()) {
		int x = que.front();
		que.pop();
		for (int i = 0; i < G2[x].size(); i++){
			int p = G2[x][i].p;
			ddd[p] = max(ddd[p], ddd[x] + G2[x][i].len);
			de[p]--;
			if (!de[p]) que.push(p);
		}
	}
	return 0;
}
int dis1[maxn];
int dis2[maxn];
int dis3[maxn];
int dis4[maxn];
int main() {

	int be1, en1, be2, en2;
	int len;
	scanf("%d %d", &n, &m);
	cin >> be1 >> en1 >> be2 >> en2;
	int be, en;
	for (int i = 0; i < m; i++) {
		scanf("%d %d %d", &be, &en, &len);
		insert(be, en, len);
		insert(en, be, len);
	}
	dijstra(be1, dis1);
	dijstra(en1, dis2);
	dijstra(be2, dis3);
	dijstra(en2, dis4);
	int ans = -1;
	for (int i = 1; i <= n; i++) {
		for (int j = 0; j < G[i].size(); j++) {
			int bee = i;
			int enn = G[i][j].p;
			int dt = G[i][j].len;
			if (dis1[bee] + dis2[enn] + dt == dis1[en1]) {
				if (dis3[bee] + dis4[enn] + dt == dis3[en2]) {//正向
					G2[bee].push_back(Node(enn, dt));
					de[enn]++;
				}
			}
		}
	}
	topu();
	memset(vis, 0, sizeof(vis));
	for (int i = 1; i <= n; i++) {
		ans = max(ddd[i], ans);
	}
	memset(ddd, 0, sizeof(ddd));
	memset(de, 0, sizeof(de));
	for (int i = 1; i <= n; i++) G2[i].clear();

	for (int i = 1; i <= n; i++) {
		for (int j = 0; j < G[i].size(); j++) {
			int bee = i;
			int enn = G[i][j].p;
			int dt = G[i][j].len;
			if (dis1[bee] + dis2[enn] + dt == dis1[en1]) {
				if (dis3[enn] + dis4[bee] + dt == dis3[en2]) {//正向
					G2[bee].push_back(Node(enn, dt));
					de[enn]++;
				}
			}
		}
	}
	topu();
	for (int i = 1; i <= n; i++) {
		ans = max(ddd[i], ans);
	}
	cout << ans << endl;
	return 0;
}