「洛谷P2891」[USACO07OPEN]吃饭Dining 解题报告

P2891 [USACO07OPEN]吃饭Dining

题目描述

Cows are such finicky eaters. Each cow has a preference for certain foods and drinks, and she will consume no others.

Farmer John has cooked fabulous meals for his cows, but he forgot to check his menu against their preferences. Although he might not be able to stuff everybody, he wants to give a complete meal of both food and drink to as many cows as possible.

Farmer John has cooked F (1 ≤ F ≤ 100) types of foods and prepared D (1 ≤ D ≤ 100) types of drinks. Each of his N (1 ≤ N ≤ 100) cows has decided whether she is willing to eat a particular food or drink a particular drink. Farmer John must assign a food type and a drink type to each cow to maximize the number of cows who get both.

Each dish or drink can only be consumed by one cow (i.e., once food type 2 is assigned to a cow, no other cow can be assigned food type 2).

翻译

有F种食物和D种饮料，每种食物或饮料只能供一头牛享用，且每头牛只享用一种食物和一种饮料。现在有N头牛，每头牛都有自己喜欢的食物种类列表和饮料种类列表，问最多能使几头牛同时享用到自己喜欢的食物和饮料。（\(1 \le F \le 100, 1 \le D \le 100, 1 \le N \le 100\)）

输入输出格式

输入格式：

Line 1: Three space-separated integers: N, F, and D

Lines 2..N+1: Each line i starts with a two integers Fi and Di, the number of dishes that cow i likes and the number of drinks that cow i likes. The next Fi integers denote the dishes that cow i will eat, and the Di integers following that denote the drinks that cow i will drink.

输出格式：

Line 1: A single integer that is the maximum number of cows that can be fed both food and drink that conform to their wishes

输入输出样例

输入样例#1：

4 3 3
2 2 1 2 3 1
2 2 2 3 1 2
2 2 1 3 1 2
2 1 1 3 3

输出样例#1：

3

---

算法

网络最大流。这里不详细讲，请大家先掌握。

思路

注意，以下出现的所有边边权皆为1，且其反向边边权为0

我们以牛、食物、饮料为点建图。

像这样：

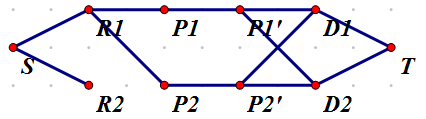
S(=0)表示额外建的一个起始点，Ri(=i+N+N)表示第i个菜，Di(=i+N+N+F)表示第i种饮料，由于牛只有一头，而网络流处理只经过一个点不方便，我们采用一种神奇方法——拆点！也就是说，把一头牛看做两个点，要匹配这头牛必须经过这头牛两点之间的边，这样就可以控制这头牛只匹配一次。如图，Pi(=i)、Pi'(=i+N)表示第i头牛。

然后建边。如图，将S与所有Ri相连，将所有的Di与T相连，S作为源点，T作为汇点。如果Pi喜欢Rj，就将Pi与Rj相连。如果Pi喜欢Dj，就将Dj与Pi'之间相连。当然，Pi与Pi'之间也要连一条边。

然后就可以套网络最大流辣。最后得出的答案即为满足的牛数。

代码

#include<bits/stdc++.h>
using namespace std;
#define open(s) freopen( s".in", "r", stdin ), freopen( s".out", "w", stdout )
#define MAXN 405
#define MAXM 40005

int N, F, D;
int hd[MAXN], nxt[MAXM << 1], to[MAXM << 1], val[MAXM << 1], tot(1);
int pre[MAXN], e[MAXN], ans, dis[MAXN];
queue<int> Q;

int x, y;
int S, T;

void Add( int x, int y, int z ){ nxt[++tot] = hd[x]; hd[x] = tot; to[tot] = y; val[tot] = z; }

bool BFS(){
	while( !Q.empty() ) Q.pop();
	memset( dis, 0, sizeof dis );
	Q.push(S); dis[S] = 1;
	while( !Q.empty() ){
		x = Q.front(); Q.pop();
		for ( int i = hd[x]; i; i = nxt[i] )
			if ( val[i] && !dis[to[i]] ){
				dis[to[i]] = dis[x] + 1;
				Q.push( to[i] );
				if ( to[i] == T ) return 1;
			}
	}
	return 0;
}

int DFS( int x, int fl ){
	if ( x == T ) return fl;
	int res(fl), k;
	for ( int i = hd[x]; i && res; i = nxt[i] ){
		if ( val[i] && dis[to[i]] == dis[x] + 1 ){
			k = DFS( to[i], min( res, val[i] ) );
			if ( !k ) dis[to[i]] = 0;
			val[i] -= k; val[i^1] += k; res -= k;
		}
	}
	return fl - res;
}

int main(){
	scanf( "%d%d%d", &N, &F, &D );
	S = 0; T = N + N + F + D + 1;
	for ( int i = 1; i <= N; ++i ) Add( i, i + N, 1 ), Add( i + N, i, 0 );
	for ( int i = 1; i <= F; ++i ) Add( S, i + N + N, 1 ), Add( i + N + N, S, 0 );
	for ( int i = 1; i <= D; ++i ) Add( i + N + N + F, T, 1 ), Add( T, i + N + N + F, 0 );
	for ( int i = 1; i <= N; ++i ){
		int f, d, x; scanf( "%d%d", &f, &d );
		for ( int j = 1; j <= f; ++j ) scanf( "%d", &x ), Add( x + N + N, i, 1 ), Add( i, x + N + N, 0 );
		for ( int j = 1; j <= d; ++j ) scanf( "%d", &x ), Add( i + N, x + N + N + F, 1 ), Add( x + N + N + F, i + N, 0 );
	}
	int t;
	while( BFS() )
		while( ( t = DFS( S, 0x7f7f7f7f ) ) > 0 ) ans += t;
	printf( "%d\n", ans );
	return 0;
}