杭电oj1995——汉诺塔V（java实现）

正文之前，先说下做这题的心路历程（简直心累）

这是今天下午的第一道题

第一次看到题目标题——汉诺塔

内心OS：wc，汉诺塔诶，听名字就很难诶，没做过诶，肯定很难实现吧，不行，我得去看看讲解

然后就上b站，看了一遍汉诺塔递归的思路，然后又搜了博客，看了汉诺塔java实现的源码（此时一下午已经过去了……）

看完了之后

内心OS：现在肯定能通过了吧

然后就把汉诺塔的实现代码照着题目改了一下提交上去了，然后……TLE

想想也对啊，那么大数据一个个统计，肯定会超时

然后就在纸上写规律，写着写着，突然发现，好像连循环都不用？？

就是这个：

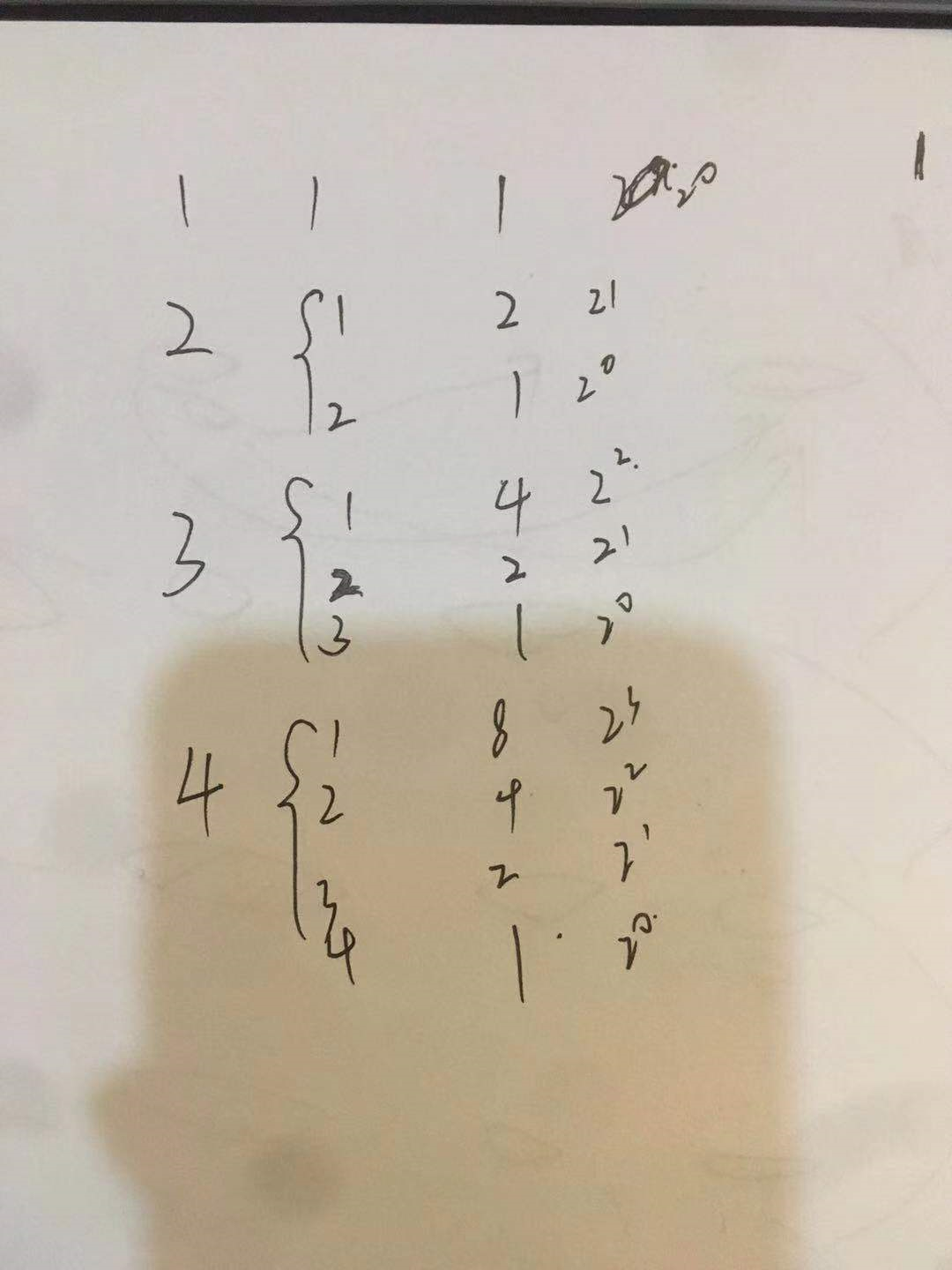
直接输出对应次方就好了……

然后我整个人都傻了！！

就，循环都不用/捂脸

总结经验：这种有限定条件的益智类游戏，肯定有规律，按照它的流程来模拟肯定会超时！

下面是源码

模拟源码：（可以作为小游戏的源码，当然，要改东西）

static int count_of_disk = 0;
    static int plate_number;

    static void hanoi(int n, Stack<Integer> stack_x, Stack<Integer> stack_y, Stack<Integer> stack_z){
        if(n==0)  return;
        hanoi(n-1,stack_x,stack_z,stack_y);
        if(stack_x.peek()==plate_number) count_of_disk++;
        stack_z.push(stack_x.pop());
        hanoi(n-1,stack_y,stack_x,stack_z);
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int count = sc.nextInt();
        while(count--!=0){
            int all_plate = sc.nextInt();
            plate_number = sc.nextInt();
            Stack<Integer> stack_x = new Stack<>();
            Stack<Integer> stack_y = new Stack<>();
            Stack<Integer> stack_z = new Stack<>();

            for(int i = all_plate;i>0;i--){//initialize
                stack_x.push(i);
            }

            hanoi(all_plate,stack_x,stack_y,stack_z);
            System.out.println(count_of_disk);
            count_of_disk = 0;

        }

下面是ac源码

public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int count = sc.nextInt();
        while(count--!=0){
            int all_plate = sc.nextInt();
            int no = sc.nextInt();
            System.out.println((long)Math.pow(2,all_plate-no));
        }
    }

对……你没看错……就是这么简单……已经ac了……

希望对大家有所帮助

以上