机器学习作业（二）逻辑回归——Python(numpy)实现

题目太长啦！文档下载【传送门】

第1题

简述：实现逻辑回归。

此处使用了minimize函数代替Matlab的fminunc函数，参考了该博客【传送门】。

 import numpy as np
 import matplotlib.pyplot as plt
 import scipy.optimize as op

 #S函数
 def sigmoid(z):
     g = 1/(1+np.exp(-z))
     return g

 #cost计算函数
 def costFunction(theta, X, y):
     theta = np.array(theta).reshape((np.size(theta),1))
     m = np.size(y)
     h = sigmoid(np.dot(X, theta))
     J = 1/m*(-np.dot(y.T, np.log(h)) - np.dot((1-y.T), np.log(1-h)))
     return J.flatten()

 def gradient(theta, X, y):
     theta = np.array(theta).reshape((np.size(theta), 1))
     m = np.size(y)
     h = sigmoid(np.dot(X, theta))
     grad = 1/m*np.dot(X.T, h - y)
     return grad.flatten()

 #读取数据，第一列是成绩1，第二列是成绩2，第三列是yes/no
 data = np.loadtxt('ex2data1.txt', delimiter=',', dtype='float')
 m = np.size(data[:, 0])
 # print(data)

 #绘制样本点
 X = data[:, 0:2]
 y = data[:, 2:3]
 pos = np.where(y == 1)[0]
 neg = np.where(y == 0)[0]
 X1 = X[pos, 0:2]
 X0 = X[neg, 0:2]
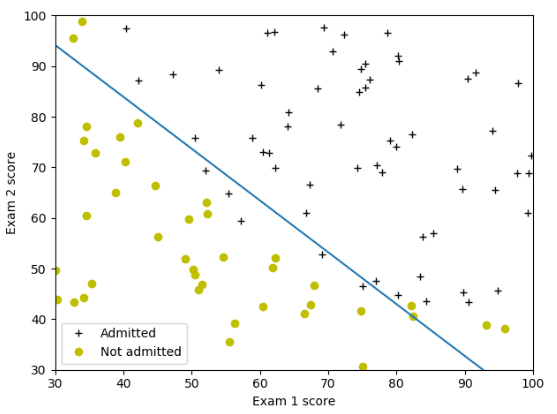
 plt.plot(X1[:, 0], X1[:, 1], 'k+')
 plt.plot(X0[:, 0], X0[:, 1], 'yo')
 plt.xlabel('Exam 1 score')
 plt.ylabel('Exam 2 score')

 #求解最优解
 one = np.ones(m)
 X = np.insert(X, 0, values=one, axis=1)
 initial_theta = np.zeros(np.size(X, 1))
 result = op.minimize(fun=costFunction, x0=initial_theta, args=(X, y), method='TNC', jac=gradient)
 # print(result)
 theta = result.x
 cost = result.fun
 print('theta:', theta)
 print('cost:', cost)

 #绘制决策边界
 plot_x = np.array([np.min(X[:, 1]), np.max(X[:, 2])])
 # print(plot_x)
 plot_y = (-1/theta[2])*(theta[1]*plot_x+theta[0])
 # print(plot_y)
 plt.plot(plot_x,plot_y)
 plt.legend(labels=['Admitted', 'Not admitted'])
 plt.axis([30, 100, 30, 100])
 plt.show()

 #预测[45 85]成绩的学生，并计算准确率
 theta = np.array(theta).reshape((np.size(theta),1))
 z = np.dot([1, 45, 85], theta)
 prob = sigmoid(z)
 print('For a student with scores 45 and 85, we predict an admission probability of ', prob)
 p = np.round(sigmoid(np.dot(X,theta)))
 acc = np.mean(p==y)*100
 print('Train Accuracy: ',acc,'%')

运行结果：

第2题

简述：通过正规化实现逻辑回归。

 import numpy as np
 import matplotlib.pyplot as plt
 import scipy.optimize as op

 #S函数
 def sigmoid(z):
     g = 1/(1+np.exp(-z))
     return g

 #cost计算函数
 def costFunction(theta, X, y, lamb):
     theta = np.array(theta).reshape((np.size(theta), 1))
     m = np.size(y)
     h = sigmoid(np.dot(X, theta))
     J = 1/m*(-np.dot(y.T, np.log(h)) - np.dot((1-y.T), np.log(1-h)))
     # 添加项
     theta2 = theta[1:, 0]
     Jadd = lamb/(2*m)*np.sum(theta2**2)
     J = J + Jadd
     return J.flatten()

 #求梯度
 def gradient(theta, X, y, lamb):
     theta = np.array(theta).reshape((np.size(theta), 1))
     m = np.size(y)
     h = sigmoid(np.dot(X, theta))
     grad = 1/m*np.dot(X.T, h - y)
     #添加项
     theta[0,0] = 0
     gradadd = lamb/m*theta
     grad = grad + gradadd
     return grad.flatten()

 #求特征矩阵
 def mapFeature(X1, X2):
     degree = 6
     out = np.ones((np.size(X1),1))
     for i in range(1, degree+1):
         for j in range(0, i+1):
             res = np.multiply(np.power(X1, i-j), np.power(X2, j))
             out = np.insert(out, np.size(out[0, :]), values=res, axis=1)
     return out

 #读取数据，第一列是成绩1，第二列是成绩2，第三列是yes/no
 data = np.loadtxt('ex2data2.txt', delimiter=',', dtype='float')
 m = np.size(data[:, 0])

 #绘制样本点
 X = data[:, 0:2]
 y = data[:, 2:3]
 pos = np.where(y == 1)[0]
 neg = np.where(y == 0)[0]
 X1 = X[pos, 0:2]
 X0 = X[neg, 0:2]
 plt.plot(X1[:, 0], X1[:, 1], 'k+')
 plt.plot(X0[:, 0], X0[:, 1], 'yo')
 plt.xlabel('Microchip Test 1')
 plt.ylabel('Microchip Test 2')
 plt.legend(labels=['y = 1', 'y = 0'])

 #数据初始化
 X = mapFeature(X[:, 0], X[:, 1])
 # print(X)
 lamb = 1
 initial_theta = np.zeros(np.size(X, 1))

 #求解最优解
 result = op.minimize(fun=costFunction, x0=initial_theta, args=(X, y, lamb), method='TNC', jac=gradient)
 # print(result)
 cost = result.fun
 theta = result.x
 print('theta:', theta)
 print('cost:', cost)

 #绘制决策边界
 u = np.linspace(-1, 1.5, 50)
 v = np.linspace(-1, 1.5, 50)
 z = np.zeros((np.size(u),np.size(v)))
 theta = np.array(theta).reshape((np.size(theta), 1))
 for i in range(0, np.size(u)):
     for j in range(0, np.size(v)):
         z[i, j] = np.dot(mapFeature(u[i], v[j]), theta)
 # print(z)
 plt.contour(u, v, z.T, [0])
 plt.show()

 #计算准确率
 p = np.round(sigmoid(np.dot(X,theta)))
 acc = np.mean(p==y)*100
 print('Train Accuracy: ',acc,'%')

运行结果：