P1282 多米诺骨牌【dp】

P1282 多米诺骨牌

提交 20.02k

通过 6.30k

时间限制 1.00s

内存限制 125.00MB

题目提供者洛谷

难度提高+/省选-

历史分数100

提交记录

查看题解

标签

 

查看算法标签

进入讨论版

相关讨论

 

查看讨论

推荐题目

 

查看推荐

 

展开

题目描述

多米诺骨牌有上下2个方块组成，每个方块中有1~6个点。现有排成行的

上方块中点数之和记为S1，下方块中点数之和记为S2，它们的差为|S1-S2|。例如在图8-1中，S1=6+1+1+1=9，S2=1+5+3+2=11，|S1-S2|=2。每个多米诺骨牌可以旋转180°，使得上下两个方块互换位置。 编程用最少的旋转次数使多米诺骨牌上下2行点数之差达到最小。

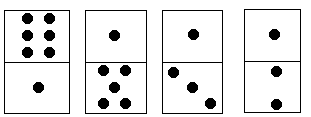
对于图中的例子，只要将最后一个多米诺骨牌旋转180°，可使上下2行点数之差为0。

输入格式

输入文件的第一行是一个正整数n(1≤n≤1000)，表示多米诺骨牌数。接下来的n行表示n个多米诺骨牌的点数。每行有两个用空格隔开的正整数，表示多米诺骨牌上下方块中的点数a和b，且1≤a，b≤6。

输出格式

输出文件仅一行，包含一个整数。表示求得的最小旋转次数。

输入输出样例

输入 #1

4
6 1
1 5
1 3
1 2

输出 #1

1

思路
　　把所有点数大的置上，对于反转过的卡牌，重量为-1，价值为 2 * (Y - X)，并增加背包原始重量；未反转的，重量为1， 体积为 2 * (X-Y);
　　f[i][j] 表示前 i 张牌的体积为 j 的最小重量。
　　
CODE

 #include <bits/stdc++.h>
 #define dbg(x) cout << #x << "=" << x << endl
 #define eps 1e-8
 #define pi acos(-1.0)

 using namespace std;
 typedef long long LL;

 template<class T>inline void read(T &res)
 {
     char c;T flag=;
     while((c=getchar())<''||c>'')if(c=='-')flag=-;res=c-'';
     while((c=getchar())>=''&&c<='')res=res*+c-'';res*=flag;
 }

 namespace _buff {
     const size_t BUFF =  << ;
     char ibuf[BUFF], *ib = ibuf, *ie = ibuf;
     char getc() {
         if (ib == ie) {
             ib = ibuf;
             ie = ibuf + fread(ibuf, , BUFF, stdin);
         }
         return ib == ie ? - : *ib++;
     }
 }

 int qread() {
     using namespace _buff;
     int ret = ;
     bool pos = true;
     char c = getc();
     for (; (c < '' || c > '') && c != '-'; c = getc()) {
         assert(~c);
     }
     if (c == '-') {
         pos = false;
         c = getc();
     }
     for (; c >= '' && c <= ''; c = getc()) {
         ret = (ret << ) + (ret << ) + (c ^ );
     }
     return pos ? ret : -ret;
 }

 int n;

 int f[][];
 bool vis[][];

 int w[];
 int v[];

 int main()
 {
     int x, y;
     scanf("%d",&n);
     int maxn = ;
     int weight = ;
     for(int i = ; i <= n; ++i) {
         scanf("%d %d",&x, &y);
         if(x > y) {
             v[i] =  * (x-y);
             w[i] = ;
             maxn += x-y;
         }
         if(y > x) {
             v[i] =  * (y-x);
             w[i] = -;
             maxn += y-x;
             weight++;
         }
     }
     for(int i = ; i <= n; ++i) {
         for(int j = ; j <= maxn; ++j) {
             f[i][j] = f[i-][j];
             vis[i][j] = vis[i-][j];
             if(vis[i-][j-v[i]] || !(j - v[i])) {
                 if(!vis[i][j]) {
                     f[i][j] = f[i-][j-v[i]] + w[i];
                     vis[i][j] = ;
                 }
                 else {
                     f[i][j] = min(f[i][j], f[i-][j-v[i]]+w[i]);
                 }
             }
         }
     }
     int q;
     for(int i = maxn; i >= ; --i) {
         if(vis[n][i]) {
             q = i;
             break;
         }
     }
     printf("%d\n",weight+f[n][q]);
     return ;
 }