洛谷P4027 [NOI2007]货币兑换

P4027 [NOI2007]货币兑换

算法：dp+斜率优化

题面十分冗长，题意大概是有一种金券每天价值会有变化，你可以在某些时间点买入或卖出所有的金券，问最大收益

根据题意，很容易列出朴素的状态转移方程:

设\(f_i\)为第\(i\)天B券的数量，\(ans_j\)为以当前价格卖光第\(j\)天的金券可获得的收益，则

\(f_i=\max{ans_j}/(a_i*r_i+b_i)\)

\(O(n)\)求\(\max{ans_j}\),复杂度为\(O(n^2)\)

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<queue>
#include<cstring>
using namespace std;
typedef long long LL;
const int MAXN=1024*100;
int N;
double S,a[MAXN],b[MAXN],r[MAXN],f[MAXN],ans;
int main(){
    scanf("%d%lf",&N,&S);
    for(int i=1;i<=N;i++){
        scanf("%lf%lf%lf",&a[i],&b[i],&r[i]);
    }
    ans=S;
    f[1]=ans*r[1]/(a[1]*r[1]+b[1]);
    for(int i=1;i<=N;i++){
        for(int j=1;j<i;j++){
            ans=max(ans,f[j]*a[i]+f[j]/r[j]*b[i]);
        }
        f[i]=ans*r[i]/(a[i]*r[i]+b[i]);
    }
    printf("%.3lf",ans);
    return 0;
}

然而此题要求\(O(nlogn)\)的做法，故朴素的dp无法AC，此时可以想到斜率优化

step1：转化方程

设\(a_i\)为第\(i\)天A券的价格，\(b_i\)为第\(i\)天B券的价格，\(ca_i\)为第\(i\)天A券的数量，\(cb_i\)为第\(i\)天B券的数量，\(f_i\)为第\(i\)天的最大收益

则\(f_i=\max{ca_j*a_i+cb_j*b_i}\)

∴如果j比k更优，有

\(ca_j*a_i+cb_j*b_i>ca_k*a_i+cb_k*b_i\)

∴\((cb_j-cb_k)*b_i>-a_i*(ca_j-ca_k)\)

∴\(\frac{cb_j-cb_k}{ca_j-ca_k}>-\frac{a_i}{b_i}\)

以\(ca\)为横坐标\(cb\)为纵坐标建立如图所示平面直角坐标系

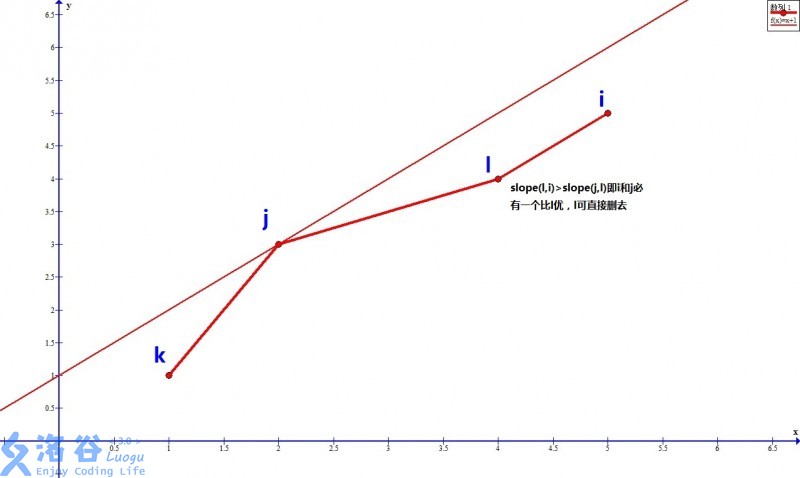
剩下的就可以-斜率优化-了

不过此题不比模板题，ca与cb不满足单调性，所以需要用平衡树或cdq等方法维护，此处用stl_set维护（因为是凸壳，所以斜率与横坐标同时满足单调性，可以用一个关键字查找）

此处切线只要找\(-\frac{a}{b}\)的lower_bound即可（代码中的query）

此处插入点要把当前位置两边的点都判断一下是否与上凸壳冲突，删除（代码中的insert）

实现就不难了

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<queue>
#include<cstring>
#include<set>
using namespace std;
typedef long long LL;
const int MAXN=1024*100;
int N;
double S,A[MAXN],B[MAXN],R[MAXN],F[MAXN],CA[MAXN],CB[MAXN];
inline double ABS(double x) { return x>0?x:-x; }
struct node {
    double X,Y,K;
    int flag;
    node() { X=Y=K=flag=0; }
    node(double x,double y) { X=x; Y=y; flag=0; }
    friend inline bool operator<(node x,node y) {
        if(x.flag||y.flag) { return x.K>y.K; }
        return x.X<y.X;
    }
    friend inline bool operator==(node x,node y) { return ABS(x.X-y.X)<1e-8; }
    friend inline double operator*(node x,node y) { return (y.Y-x.Y)/(y.X-x.X); }//斜率
    inline bool error() { return X<-1e20||Y<-1e20; }
} error(-1e21,-1e21);
set<node> dq;
typedef set<node>::iterator ITER;
inline node next(node x) {
    ITER ii=dq.upper_bound(x);
    return ii==dq.end()?error:*ii;
}
inline node lower(node x) {
    ITER ii=dq.lower_bound(x);
    return ii==dq.end()?error:*ii;
}
inline node pre(node x) {
    ITER ii=dq.lower_bound(x);
    return ii==dq.begin()?error:*(--ii);
}
inline void insert(node x) {
    if(dq.empty()) {
        x.K=0;
        dq.insert(x);
        return;
    }
    node L=pre(x),R=lower(x);
    if((L.error()&&x.Y<R.Y)||(!L.error()&&!R.error()&&L*x-L*R<1e-8)/**/||(x==R)) { return; }
    R=next(x);
    while(1) {
        L=R;
        R=next(L);
        if(L.error()||R.error()||(x*L)-(L*R)>=1e-8) { break; }
        dq.erase(L);
    }
    L=pre(x);
    while(1) {
        R=L;
        L=pre(R);
        if(L.error()||R.error()||(L*R)-(R*x)>=1e-8) { break; }
        dq.erase(R);
    }
    L=pre(x);
    R=next(x);
    x.K=(L.error()?0:(L*x));
    dq.insert(x);
    if(!R.error()) {
        dq.erase(R);
        R.K=(x*R);
        dq.insert(R);
    }
}
inline double query(double x,double y) {
    node ii;
    ii.flag=1;
    ii.K=-x/y;
    ii=*(--dq.lower_bound(ii));
    return ii.error()?0:ii.X*x+ii.Y*y;
}
int main() {
    scanf("%d%lf",&N,&S);
    for(int i=1; i<=N; i++) {
        scanf("%lf%lf%lf",&A[i],&B[i],&R[i]);
    }
    F[1]=S;
    CB[1]=S/(A[1]*R[1]+B[1]);
    CA[1]=CB[1]*R[1];
    insert(node(CA[1],CB[1]));
    for(int i=2; i<=N; i++) {
        F[i]=max(F[i-1],query(A[i],B[i]));
        CB[i]=F[i]/(A[i]*R[i]+B[i]);
        CA[i]=CB[i]*R[i];
        insert(node(CA[i],CB[i]));
    }
    printf("%.3lf",F[N]);
    return 0;
}