洛谷 P2114 [NOI2014]起床困难综合症

题目描述

21世纪，许多人得了一种奇怪的病：起床困难综合症，其临床表现为：起床难，起床后精神不佳。作为一名青春阳光好少年，atm一直坚持与起床困难综合症作斗争。通过研究相关文献，他找到了该病的发病原因：在深邃的太平洋海底中，出现了一条名为drd的巨龙，它掌握着睡眠之精髓，能随意延长大家的睡眠时间。正是由于drd的活动，起床困难综合症愈演愈烈，以惊人的速度在世界上传播。为了彻底消灭这种病，atm决定前往海底，消灭这条恶龙。历经千辛万苦，atm终于来到了drd所在的地方，准备与其展开艰苦卓绝的战斗。drd有着十分特殊的技能，他的防御战线能够使用一定的运算来改变他受到的伤害。具体说来，drd的防御战线由n扇防御门组成。每扇防御门包括一个运算op和一个参数t，其中运算一定是OR,XOR,AND中的一种，参数则一定为非负整数。如果还未通过防御门时攻击力为x，则其通过这扇防御门后攻击力将变为x op t。最终drd受到的伤害为对方初始攻击力x依次经过所有n扇防御门后转变得到的攻击力。

由于atm水平有限，他的初始攻击力只能为0到m之间的一个整数（即他的初始攻击力只能在 0, 1, … , m中任选，但在通过防御门之后的攻击力不受m的限制）。为了节省体力，他希望通过选择合适的初始攻击力使得他的攻击能让drd受到最大的伤害，请你帮他计算一下，他的一次攻击最多能使drd受到多少伤害。

输入输出格式

输入格式：

输入文件的第 1 行包含 2 个整数，依次为n, m，表示 drd 有n扇防御门，atm 的初始攻击力为0到m之间的整数。

接下来n行，依次表示每一扇防御门。每行包括一个字符串op和一个非负整数t，两者由一个空格隔开，且op在前，t在后，op表示该防御门所对应的操作，t表示对应的参数。

输出格式：

输出一行一个整数，表示atm的一次攻击最多使drd受到多少伤害。

输入输出样例

输入样例#1：复制

3 10

AND 5

OR 6

XOR 7

输出样例#1：复制

说明

【样例说明】

atm可以选择的初始攻击力为 0,1, … ,10。

假设初始攻击力为 4，最终攻击力经过了如下计算

4 AND 5 = 4

4 OR 6 = 6

6 XOR 7 = 1

类似的，我们可以计算出初始攻击力为 1,3,5,7,9 时最终攻击力为 0，初始攻击力为 0,2,4,6,8,10 时最终攻击力为 1，因此atm的一次攻击最多使drd受到的伤害值为1。

【数据规模与约定】

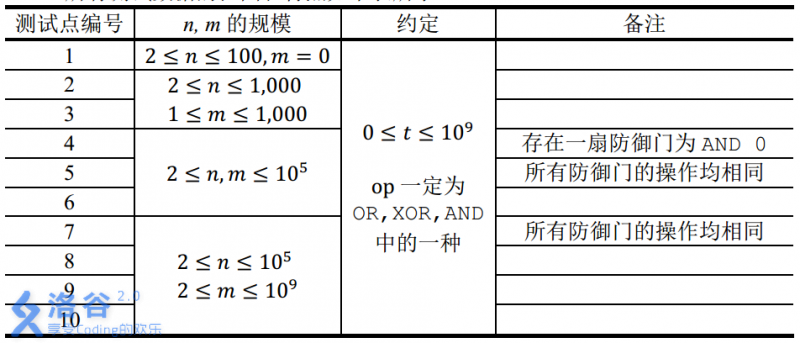
题解

这道题是位运算的基础题，思维和代码难度都不高

本题的困难在于给定的数较大，无法枚举，所以就必须利用位运算的一个特性：当前位的运算不会影响其他的位

根据这个特性，可以将每一位单独枚举，然后再贪心选择答案即可

对于每一扇防御门，我们需要关心的只是某一位原来是1或0在进去之后变成了1还是0

于是我们可以将每一位都是1的$0x7fffffff$和每一位都是0的$0$代入，得出两个结果，只要将原数的位&得出的结果就可以得到1或0经过操作的结果，无非就是4种

$0\rightarrow 0,1\rightarrow 0$

$0\rightarrow 0,1\rightarrow 1$

$0\rightarrow 1,1\rightarrow 0$

$0\rightarrow 1,1\rightarrow 1$

然后贪心讨论就行了：

对于一位，如果$0\rightarrow 1$，那么果断选择0，统计答案；

否则如果$1\rightarrow 1$并且能选，则选，统计答案并将当前位减掉

 #include<bits/stdc++.h>

 using namespace std;

 typedef long long LL;

 const int MAXL=,MAXD=;

 LL Ful=0x7fffffff/*full*/,Ept/*empty*/,cur,M,ans;

 char str[MAXL];

 int N;

 int main(){

     scanf("%d%lld",&N,&M);

     for(int i=;i<=N;i++){

         scanf("%s %lld",str,&cur);

         if(!strcmp(str,"AND")){

             Ful&=cur;

             Ept&=cur;

         }else if(!strcmp(str,"OR")){

             Ful|=cur;

             Ept|=cur;

         }else{

             Ful^=cur;

             Ept^=cur;

         }

     }

     for(LL i=MAXD;i>=;i--){

         if(Ept&(<<i)){/*0 -> 1*/

             ans+=<<i;

         }else if((M>=(<<i))&&(Ful&(<<i))){

             M-=<<i;

             ans+=<<i;

         }

     }

     printf("%lld",ans);

     return ;

 }