[NOIP2019模拟赛]LuoguP4261白金元首与克劳德斯

题目描述

给出坐标系中n个矩形，类型1的矩形每单位时间向x轴正方向移动1个单位，类型2的矩形向y轴正方向，初始矩形不重叠，一个点被矩形覆盖当且仅当它在矩形内部（不含边界），求$(-\infty ,+\infty)$时间内一个点被覆盖的最多矩形数量。n<=10^5。

分析

部分分给的可真多，$n^2$就能拿80pts（然而我n==2的特判打错了(不知道为什么我puts("0")了qwq）变成70pts）

首先:我们可以把竖着运动的矩形看成静止不动，把横着运动的矩形看成延斜率k=-1的直线运动的矩形

　　因为一开始没有重复矩形，所以最后最多只有两个重复，所以答案不是1，就是2

　　所以我们输出rand()%2+1

　　考试的时候把这道题当做计算几何做了...

考虑$n^2$做法：

　　由上面的分析可以得到，如果答案为2，只有这三种情况：

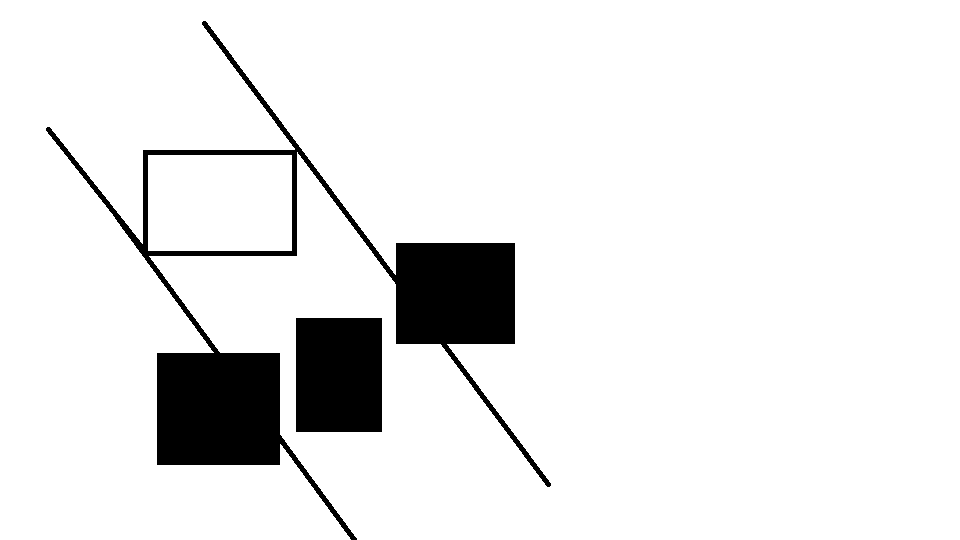
　　分别枚举每一个0的矩形和1的矩形判断有没有重叠就好了

　　注意check的时候能不能取等号

考虑优化：

　　显然我们可以把这题转换成区间覆盖，每个矩形变成这样的线段：

$$(x_2-x_1-w_1,x_2+w_2-x_1)$$

和

$$(y_1-y_2-h_2,y_1+h_1-y_2)$$

然后化简一下，用贪心做区间覆盖就好了（比我打的$n^2$还简单。。。）

 #include<bits/stdc++.h>
 using namespace std;
 inline int read(){
     int ans=,f=;char chr=getchar();
     while(!isdigit(chr)){if(chr=='-')f=-;chr=getchar();}
     while(isdigit(chr)) {ans=(ans<<)+(ans<<)+chr-;chr=getchar();}
     return ans*f;
 }const int M = 1e5+;
 int n,T,n1,n2;
 //-----------------------------------n^2暴力做法------------------------------------
 struct P{int x,y,w,h;}a[M],b[M];
 struct Poi{int x,y;};
 struct Line{int a[];}ll[M];
 int L[M];
 int s[][];
 inline bool check_up(Poi x,int l){
     int y=-x.x+l;
     if(x.y>y) return ;
     return ;
 }
 inline bool check_down(Poi x,int l){
     int y=-x.x+l;
     if(x.y<y) return ;
     return ;
 }
 inline bool check(Poi x,Poi y,int l1,int l2){
     int y1=-x.x+l1,y2=-y.x+l2;
     if(x.y>=y1&&y.y<=y2) return ;
     return ;
 }
 inline void Solve_1(){
     n=read();n1=,n2=;
     for(int i=;i<=n;i++){
         int x=read(),y=read(),w=read(),h=read(),d=read();
         if(d==)
             a[++n1]=(P){x,y,w,h};
         else b[++n2]=(P){x,y,w,h};
     }
     for(int i=;i<=n1;i++){
         ll[i].a[]=a[i].x+a[i].y;
         ll[i].a[]=a[i].x+a[i].y+a[i].w+a[i].h;
     }int ff=;
     for(int i=;i<=n2;i++){
         Poi A,B;
         A=(Poi){b[i].x,b[i].y};
         B=(Poi){b[i].x+b[i].w,b[i].y+b[i].h};
         for(int j=;j<=n1;j++){
             if(check_down(A,ll[j].a[])&&check_up(B,ll[j].a[])||
                check_down(A,ll[j].a[])&&check_up(B,ll[j].a[])||
                check(A,B,ll[j].a[],ll[j].a[]))
                 {ff=;break;}
         }
     }if(!ff) puts("");else puts("");
 }
 //--------------------------------------------------------------------------------------------
 int lst[M],ff;
 struct PP{int x,y,type;}seg[M];
 bool cmp(const PP&a,const PP&b){return a.x==b.x&&a.y<b.y||a.x<b.x;}
 inline void Solve(){
     n=read(),ff=;
     for(int i=;i<=n;i++){
         int x=read(),y=read(),w=read(),h=read(),d=read();
         seg[i]=(PP){x+y,x+y+w+h,d};
     }sort(seg+,seg+n+,cmp);
     memset(lst,-0x3f,sizeof(lst));
     for(int i=;i<=n;i++){
         if(seg[i].x<lst[seg[i].type^]){
             puts("");
             ff=;break;
         }lst[seg[i].type]=max(lst[seg[i].type],seg[i].y);
     }if(!ff)puts("");
 }
 int main(){
     freopen("cloud.in","r",stdin);
     freopen("cloud.out","w",stdout);
     T=read();
     while(T--){
 //        Solve_1();
         Solve();
     }
     return ;
 }