【做题笔记】[NOIOJ，非NOIp原题]装箱问题

题意：给定一些矩形，面积分别是 \(1\times 1,2\times 2,3\times 3,4\times 4,5\times 5,6\times 6\)。您现在知道了这些矩形的个数 \(a,b,c,d,e,f\)，需要将这些矩形一个不落的装到一种面积为 \(6\times 6\)的大矩形里面，问如何使大矩形的数量最少（输入包含多组数据，以全部都是 0 结尾）。

样例输入：

0 0 4 0 0 1
7 5 1 0 0 0
0 0 0 0 0 0

样例输出：

2
1

分组考虑，首先，我们知道对于 \(6\times 6,5\times 5,4\times 4\)的矩形一个大矩形中只能占一个。如图

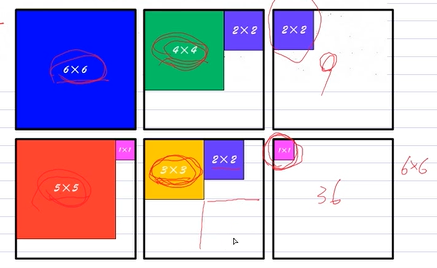
于是设每次答案为 \(\text{ans}\)，则答案最少为 \(\text{ans+d+e+f}\)。

顺着刚刚的思路，单独考虑对于 \(3\times 3\)的情况。不难发现，一个大矩形最多可以接纳 4 个 \(3\times 3\) 的矩形，换而言之，4 个这样的小矩形占用一个大矩形。考虑到余数，则答案需再加上 \((c+3)/4\)。（补 3 除 4，在本题中这是一个很重要的思路）。

于是当前答案有：int ans=(d+e+f+(c+3)/4);

接着，考虑面积为 \(2\times 2\) 的矩形的情况。注意到被蓝色和红色区域“占领”的面积都无法接纳 \(2\times 2\)的矩形，那么考虑已经装入 \(4\times 4\) 和 \(3\times 3\) 的。 \(4\times 4\)的比较好想，显而易见的最多只能填入 5 个。对于 \(3\times 3\) 的矩形，分别考虑装入一个 \(3\times 3\)，两个 \(3\times 3\) 和三个 \(3\times 3\) 的情况。思考可以发现对应的答案分别为 \(5,3,1\) 。由于 \(3\times 3\) 的数量不确定，可以开一个数组记录，即 int mod[4]={0,5,3,1};，然后设变量 \(y\) 为当前答案下最多能装入的 \(2\times 2\) 的数量，把这个值与输入的 \(2\times 2\) 的数量作比较，若比输入的数量少，则说明剩下的此类型的矩形只有单独放。根据“补 3 除 4”的原则易得还需加上的新矩形为 (b-y+8)/9 个。

最后，考虑 \(1\times 1\) 的矩形。这种矩形很特殊，我们分析发现它的一个性质——它不涉及填入后留空位的问题。啥意思呢？也就是说，我们采用“见缝插针”的方式，即，有多少空就都填满。但是，如果还像上面那样加加除除的话太麻烦了，于是，考虑如下的算法：

首先考虑，对于当前答案的所有面积，若都填一，则能填多少；然后减去其他占用的面积，最后按照如上的方式比较是否需要新增。

以上，就是本题的贪心策略。自证不难

#include <iostream>
#include <cstdio>

using namespace std;

int mod[4]={0,5,3,1};

int main()
{
    int a,b,c,d,e,f;
    while(1)
    {
        cin>>a>>b>>c>>d>>e>>f;
        if(!a&&!b&&!c&&!d&&!e&&!f)break;
        int ans=(d+e+f+(c+3)/4);
        int y=5*d+mod[c%4];
        if(b>y)ans+=(b-y+8)/9;
        int x=36*ans-(36*f+25*e+16*d+9*c+4*b);
        if(a>x)ans+=(a-x+35)/36;
        cout<<ans<<endl;
    }
    return 0;
}
/*
data:
0 0 4 0 0 1
7 5 1 0 0 0
0 0 0 0 0 0
*/