C++ TrieTree（字典树）容器的实现

最近研究了一下C++线程池，在网上看了一下别人的代码，写的很不错，参见：http://www.cnblogs.com/lidabo/p/3328646.html

其中，他用了STL的set容器管理线程池中的线程，在线程池运行的过程中需要频繁的进行插入、查找和删除的操作，我个人觉得这些操作会是线程池中的很大的时间开销，想起了大学老师讲过的一个TireTree(字典树)的数据结构，利用多叉树

可以快速的实现元素的插入、查找和删除，稍加改动也可以支持自动排序，唯一的缺点就是多叉树的结构空间开销较大，所以要控制好内存操作，防止内存泄露。

经测试，再插入元素和删除元素的方面，TrieTree比set有明显优势，在相同的元素数量下，内存开销也不过是set的1.5~2倍，时间却是1/10左右。

 #ifndef _MY_TRIE_TREE
 #define _MY_TRIE_TREE

 template<class T,class K>
 class TrieTree{
 public:
     TrieTree();
     virtual ~TrieTree();
     bool insert(T *data,K key,bool overwrite = false);
     bool remove(K key,bool free_memory = false);
     bool find(K key,T *& pData);
 private:
     enum
     {
         Dimension = ,
     };
     typedef struct tagNode
     {
         tagNode *child[Dimension];
         T *data;
         tagNode()
         {
             for(int i = ;i < Dimension;i++)
             {
                 child[i] = NULL;
             }
             data = NULL;
         }
         ~tagNode()
         {
             if(child == NULL)
             {
                 delete[] child;
             }
             if(data != NULL)
             {
                 delete data;
             }
         }
     }Node;
     Node *m_pHead;
     unsigned int m_nElementCnt;
     unsigned int m_nNodeCnt;
     void destory(Node *p_head);
 public:
     void free();
     void dump();
     void trival( Node *pNode,int &nodeCnt );
 };

 template<class T,class K>
 bool TrieTree<T, K>::find( K key,T *& pData )
 {
     int m = ;
     Node **p_find = NULL;
     if(m_pHead == NULL)
     {
         return false;
     }
     p_find = &m_pHead;
     while( key >  )
     {
         m = key%;
         if((*p_find) != NULL)
         {
             p_find = &(*p_find)->child[m];
         }
         else
         {
             break;
         }
         key /= ;
     }
     if((*p_find) != NULL)
     {
         // 数据为空
         if((*p_find)->data == NULL)
         {
             return false;
         }
         pData = (*p_find)->data;
         return true;
     }
     else
     {
         return false;
     }
 }

 template<class T,class K>
 void TrieTree<T, K>::free()
 {
     destory(m_pHead);
 }

 template<class T,class K>
 void TrieTree<T, K>::destory( Node *p_head )
 {
     if(p_head != NULL)
     {
         for(int i = ;i < Dimension;i++)
         {
             destory(p_head->child[i]);
         }
         delete p_head;
         m_nNodeCnt--;
     }
 }

 template<class T,class K>
 void TrieTree<T, K>::trival( Node *pNode,int &nodeCnt )
 {
     if(pNode != NULL)
     {
         nodeCnt++;
         if(pNode->data != NULL)
         {
             //cout<<*(pNode->data)<<" ";
         }
         for(int i = ;i < Dimension;i++)
         {
             trival(pNode->child[i],nodeCnt);
         }
     }
 }

 template<class T,class K>
 void TrieTree<T, K>::dump()
 {
     int nodeCnt = ;
     trival(m_pHead,nodeCnt);
     cout<<endl;
     //cout<<endl<<"size = "<<sizeof(Node)<< " * "<<nodeCnt<<" = "<<sizeof(Node)*nodeCnt<<endl;
     //cout<<endl<<"data = "<<sizeof(T)<< " * "<<m_nElementCnt<<" = "<<sizeof(T)*m_nElementCnt<<endl;
     //cout<<endl<<"rate = "<<((double)sizeof(T) * m_nElementCnt)/(sizeof(Node)*nodeCnt)<<endl;
     cout<<"m_nNodeCnt = "<<m_nNodeCnt;
     cout<<",m_nElementCnt = "<<m_nElementCnt;
     cout<<",nodeCnt = "<<nodeCnt<<endl;
 }

 template<class T,class K>
 TrieTree<T,K>::TrieTree()
 {
     m_pHead = new Node();
     m_nElementCnt = ;
     m_nNodeCnt = ;
 }

 template<class T,class K>
 TrieTree<T,K>::~TrieTree()
 {
     destory(m_pHead);
 }

 template<class T,class K>
 bool TrieTree<T, K>::remove( K key ,bool free_memory)
 {
     int m = ;
     Node **p_find = NULL;
     if(m_pHead == NULL)
     {
         return false;
     }
     p_find = &m_pHead;
     while( key >  )
     {
         m = key%;
         if((*p_find) != NULL)
         {
             p_find = &(*p_find)->child[m];
         }
         else
         {
             break;
         }
         key /= ;
     }
     if((*p_find) != NULL)
     {
         // 不释放节点空间
         if( free_memory == false )
         {
             if((*p_find)->data == NULL)
             {
                 return false;
             }
             delete (*p_find)->data;
             (*p_find)->data = NULL;
             m_nElementCnt--;
             return true;
         }
         // 释放节点空间
         else
         {
             //并不是所有节点都能释放，没有子节点的节点才能释放
             bool hasChild  = false;
             for(int i = ;i < Dimension;i++)
             {
                 if((*p_find)->child[i] != NULL)
                 {
                     hasChild = true;
                 }
             }
             // 释放节点,直接delete
             if(hasChild == false)
             {
                 delete (*p_find);
                 (*p_find) = NULL;
                 m_nElementCnt--;
                 m_nNodeCnt--;
             }
             // 不能释放节点，释放data，data = NULL
             else
             {
                 if((*p_find)->data == NULL)
                 {
                     return false;
                 }
                 T *pData = (*p_find)->data;
                 (*p_find)->data = NULL;
                 delete pData;
                 pData = NULL;
                 m_nElementCnt--;
                 return true;
             }
         }
     }
     else
     {
         return false;
     }
 }

 template<class T,class K>
 bool TrieTree<T, K>::insert( T *data,K key,bool overwrite)
 {
     int m = ;
     Node **p_find = NULL;
     if(m_pHead == NULL)
     {
         return false;
     }
     p_find = &m_pHead;
     while( key >  )
     {
         m = key%;
         if((*p_find) == NULL)
         {
             (*p_find) = new Node();
             m_nNodeCnt++;
         }
         p_find = &(*p_find)->child[m];
         key /= ;
     }
     if((*p_find) == NULL)
     {
         (*p_find) = new Node();
         (*p_find)->data = data;
         m_nNodeCnt++;
         m_nElementCnt++;
         return true;
     }
     else
     {
         if((*p_find)->data == NULL)
         {
             (*p_find)->data = data;
             m_nElementCnt++;
             return true;
         }
         else
         {
             if(overwrite == false)
             {
                 return false;
             }
             else
             {
                 (*p_find)->data = data;
                 m_nElementCnt++;
                 return true;
             }
         }
     }
 }

 #endif

测试代码：

void test1()
{
    int cnt = ;
    time_t s,e;
    int n = ,m = ;
    TrieTree<R,int> a;
    set<R*> b;
    for(m = ;m < ;m++)
    {
        cout<<"item count:"<<n<<endl;
        s = clock();
        for(int i = ;i < n;i++)
        {
            R *r = new R(i);
            a.insert(r,i);
        }
        //a.dump();
        for(int i = ;i < n/;i++)
        {
            a.remove(i,true);
        }
        e = clock();
        cout<<"TrieTree Use Time:"<<e-s<<endl;
        s = clock();
        for(int i = ;i < n;i++)
        {
            R *r = new R(i);
            b.insert(r);
        }
        b.clear();
        e = clock();
        cout<<"Set Use Time:"<<e-s<<endl;
        cout<<"-------------------"<<endl;
        n*=;
    }
}
int main()
{
    test1();
    system("pause");
    return ;
}

测试结果：

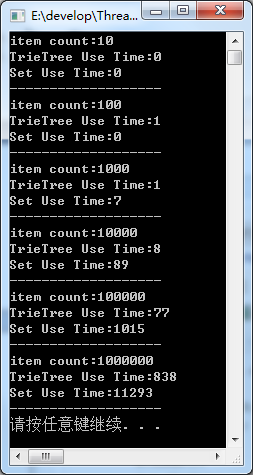
以上仅是我个人的观点，代码也仅仅是练练手而已，不保证理论和实现完全正确，仅供参考。