cf.VK CUP 2015.B.Mean Requests

Mean Requests

time limit per test

4 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

In this problem you will have to deal with a real algorithm that is used in the VK social network.

As in any other company that creates high-loaded websites, the VK developers have to deal with request statistics regularly. An important indicator reflecting the load of the site is the mean number of requests for a certain period of time of T seconds (for example, T = 60 seconds = 1 min and T = 86400 seconds = 1 day). For example, if this value drops dramatically, that shows that the site has access problem. If this value grows, that may be a reason to analyze the cause for the growth and add more servers to the website if it is really needed.

However, even such a natural problem as counting the mean number of queries for some period of time can be a challenge when you process the amount of data of a huge social network. That's why the developers have to use original techniques to solve problems approximately, but more effectively at the same time.

Let's consider the following formal model. We have a service that works for n seconds. We know the number of queries to this resourcea_t at each moment of time t (1 ≤ t ≤ n). Let's formulate the following algorithm of calculating the mean with exponential decay. Let c be some real number, strictly larger than one.

// setting this constant value correctly can adjust    // the time range for which statistics will be calculated double c = some constant value; 
// as the result of the algorithm's performance this variable will contain  // the mean number of queries for the last  // T seconds by the current moment of time double mean = 0.0; 
for t = 1..n: // at each second, we do the following:     // at is the number of queries that came at the last second;     mean = (mean + at / T) / c;

Thus, the mean variable is recalculated each second using the number of queries that came at that second. We can make some mathematical calculations and prove that choosing the value of constant c correctly will make the value of mean not very different from the real mean value a_x at t - T + 1 ≤ x ≤ t.

The advantage of such approach is that it only uses the number of requests at the current moment of time and doesn't require storing the history of requests for a large time range. Also, it considers the recent values with the weight larger than the weight of the old ones, which helps to react to dramatic change in values quicker.

However before using the new theoretical approach in industrial programming, there is an obligatory step to make, that is, to test its credibility practically on given test data sets. Your task is to compare the data obtained as a result of the work of an approximate algorithm to the real data.

You are given n values a_t, integer T and real number c. Also, you are given m moments p_j (1 ≤ j ≤ m), where we are interested in the mean value of the number of queries for the last T seconds. Implement two algorithms. The first one should calculate the required value by definition, i.e. by the formula 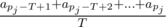. The second algorithm should calculate the mean value as is described above. Print both values and calculate the relative error of the second algorithm by the formula 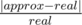, where approx is the approximate value, obtained by the second algorithm, and real is the exact value obtained by the first algorithm.

Input

The first line contains integer n (1 ≤ n ≤ 2·10⁵), integer T (1 ≤ T ≤ n) and real number c (1 < c ≤ 100) — the time range when the resource should work, the length of the time range during which we need the mean number of requests and the coefficient c of the work of approximate algorithm. Number c is given with exactly six digits after the decimal point.

The next line contains n integers a_t (1 ≤ a_t ≤ 10⁶) — the number of queries to the service at each moment of time.

The next line contains integer m (1 ≤ m ≤ n) — the number of moments of time when we are interested in the mean number of queries for the last T seconds.

The next line contains m integers p_j (T ≤ p_j ≤ n), representing another moment of time for which we need statistics. Moments p_j are strictly increasing.

Output

Print m lines. The j-th line must contain three numbers real, approx and error, where:

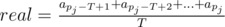•  is the real mean number of queries for the last T seconds;
• approx is calculated by the given algorithm and equals mean at the moment of time t = p_j (that is, after implementing the p_j-th iteration of the cycle);
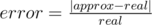•  is the relative error of the approximate algorithm.

The numbers you printed will be compared to the correct numbers with the relative or absolute error 10^- 4. It is recommended to print the numbers with at least five digits after the decimal point.

Sample test(s)

input

1 1 2.000000 1 1 1

output

1.000000 0.500000 0.500000

input

11 4 1.250000 9 11 7 5 15 6 6 6 6 6 6 8 4 5 6 7 8 9 10 11

output

8.000000 4.449600 0.443800 9.500000 6.559680 0.309507 8.250000 6.447744 0.218455 8.000000 6.358195 0.205226 8.250000 6.286556 0.237993 6.000000 6.229245 0.038207 6.000000 6.183396 0.030566 6.000000 6.146717 0.024453

input

13 4 1.250000 3 3 3 3 3 20 3 3 3 3 3 3 3 10 4 5 6 7 8 9 10 11 12 13

output

3.000000 1.771200 0.409600 3.000000 2.016960 0.327680 7.250000 5.613568 0.225715 7.250000 5.090854 0.297813 7.250000 4.672684 0.355492 7.250000 4.338147 0.401635 3.000000 4.070517 0.356839 3.000000 3.856414 0.285471 3.000000 3.685131 0.228377 3.000000 3.548105 0.182702
我看不懂关于real的那个公式。后来发现他是前T个的mean，orz

 #include<stdio.h>
 #include<string.h>
 #include<math.h>
 using namespace std;
 typedef long long ll ;
 const int M =  * 1e5 +  ;
 int a [M] ;
 int n , T , m;
 double c ;
 double real , mean , error ;

 int main ()
 {
    //    freopen ("a.txt" , "r" , stdin ) ;
     scanf ("%d%d%lf" , &n , &T , &c) ;
     for (int i =  ; i <= n ; i++) {
         scanf ("%d", &a[i] ) ;
     }
     scanf ("%d" , &m) ;

         int b[M] ;
         for (int i =  ; i <= m ; i++) {
             scanf ("%d" , &b[i]) ;
         }
     double sum =  ;
     double mean =  ;
     int k =  ;
     for (int i =  ; i <= n ; i++) {
         sum += a[i] ;
         if (i > T) {
             sum -= a[i - T] ;
         }
         mean = (double) 1.0 * (mean + 1.0 * a[i] / T) / c ;
         if (i == b[k]) {
             real = 1.0 * sum / T ;
             error = fabs (real - mean) / real ;
             printf ("%.6f %.6f %.6f\n" , real , mean , error ) ;
             k++ ;
         }
     }
     return  ;
 }