【POJ】3150 Cellular Automaton（矩阵乘法+特殊的技巧）

http://poj.org/problem?id=3150

这题裸的矩阵很容易看出，假设d=1，n=5那么矩阵是这样的

1 1 0 0 1

1 1 1 0 0

0 1 1 1 0

0 0 1 1 1

1 0 0 1 1

这是n^3的，可是n<=500，显然tle

我们观察这个n×n的矩阵，发现没一行都是由上一行向右移得到的。

而根据Cij=Aik×Bkj，我们可以发现，其实Bkj==Akj==Ai(j-k)

那么就可以降二维变一维，每一次只要算第一行即可，即Cj=Ak*Bj-k

#include <cstdio>
#include <cstring>
#include <cmath>
#include <string>
#include <iostream>
#include <algorithm>
using namespace std;
#define rep(i, n) for(int i=0; i<(n); ++i)
#define for1(i,a,n) for(int i=(a);i<=(n);++i)
#define for2(i,a,n) for(int i=(a);i<(n);++i)
#define for3(i,a,n) for(int i=(a);i>=(n);--i)
#define for4(i,a,n) for(int i=(a);i>(n);--i)
#define CC(i,a) memset(i,a,sizeof(i))
#define read(a) a=getint()
#define print(a) printf("%d", a)
#define dbg(x) cout << #x << " = " << x << endl
#define printarr(a, n, m) rep(aaa, n) { rep(bbb, m) cout << a[aaa][bbb]; cout << endl; }
inline const long long getint() { long long r=0, k=1; char c=getchar(); for(; c<'0'||c>'9'; c=getchar()) if(c=='-') k=-1; for(; c>='0'&&c<='9'; c=getchar()) r=r*10+c-'0'; return k*r; }
inline const int max(const int &a, const int &b) { return a>b?a:b; }
inline const int min(const int &a, const int &b) { return a<b?a:b; }
typedef long long matrix[505];
void mul(matrix a, matrix b, matrix c, int lb, int lc, long long md) {
	matrix t;
	rep(j, lc) {
		t[j]=0;
		rep(k, lb)
			if(j-k>=0) t[j]=(t[j]+a[k]*b[j-k])%md;
			else t[j]=(t[j]+a[k]*b[lb+j-k])%md;
	}
	rep(j, lc) c[j]=t[j];
}
matrix a, b, c;
int main() {
	long long n, m, d, k;
	cin >> n >> m >> d >> k;
	rep(i, n) read(c[i]);
	a[0]=b[0]=1;
	rep(j, d+1) a[j]=1;
	for2(j, n-d, n) a[j]=1;
	while(k) {
		if(k&1) mul(a, b, b, n, n, m);
		mul(a, a, a, n, n, m);
		k>>=1;
	}
	mul(c, b, c, n, n, m);
	rep(i, n) printf("%lld ", c[i]);
	return 0;
}

---

Description

A cellular automaton is a collection of cells on a grid of specified shape that evolves through a number of discrete time steps according to a set of rules that describe the new state of a cell based on the states of neighboring cells. The order of the cellular automaton is the number of cells it contains. Cells of the automaton of order n are numbered from 1 to n.

The order of the cell is the number of different values it may contain. Usually, values of a cell of order m are considered to be integer numbers from 0 to m − 1.

One of the most fundamental properties of a cellular automaton is the type of grid on which it is computed. In this problem we examine the special kind of cellular automaton — circular cellular automaton of order n with cells of order m. We will denote such kind of cellular automaton as n,m-automaton.

A distance between cells i and j in n,m-automaton is defined as min(|i − j|, n − |i − j|). A d-environment of a cell is the set of cells at a distance not greater than d.

On each d-step values of all cells are simultaneously replaced by new values. The new value of cell i after d-step is computed as a sum of values of cells belonging to the d-enviroment of the cell i modulo m.

The following picture shows 1-step of the 5,3-automaton.

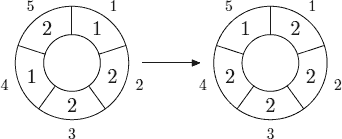
The problem is to calculate the state of the n,m-automaton after k d-steps.

Input

The first line of the input file contains four integer numbers n, m, d, and k (1 ≤ n ≤ 500, 1 ≤ m ≤ 1 000 000, 0 ≤ d < ⁿ⁄₂ , 1 ≤ k ≤ 10 000 000). The second line contains n integer numbers from 0 to m − 1 — initial values of the automaton’s cells.

Output

Output the values of the n,m-automaton’s cells after k d-steps.

Sample Input

sample input #1
5 3 1 1
1 2 2 1 2

sample input #2
5 3 1 10
1 2 2 1 2

Sample Output

sample output #1
2 2 2 2 1

sample output #2
2 0 0 2 2

Source

Northeastern Europe 2006