洛谷 P2009 跑步

P2009 跑步

题目背景

跑步是一项有意思的运动，尤其是可以开发人的脑筋。常神牛很喜欢跑步。

题目描述

常神牛跑步的场地是一个多边形（边数≤20，每个顶点用英文大写字母表示），并且在这个多边形内部，还会有一些小道，连接两个不相邻的顶点。所有的边长和小道都是双向通行的举例来说，下面一个图：

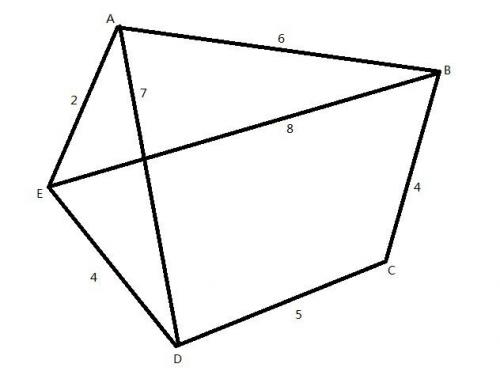
假设常神牛从A点跑到D点，最短的路径是A-E-D（长度为6）。

现在告诉你多边形的边数n，多边形每条边的长度，多边形内的连线数k，每条连线的两个端点及长度，以及起始点和结束点，请你输出最短路径的长度。但是常神牛有点强迫症，如果两点之间有多条道路直接连接，他会选择最长的那条。

注意：输入数据不保证起点和终点不同，也不保证小道的起点和终点不同。在读入过程中，如果两点之间有多条小道，那么它们间的距离为这些小道的最大值。所以，如果读入一个小道起点和终点相同，那么这个点到它本身的距离不为0。

输入输出格式

输入格式：

输入文件为run.in。

第一行，2个数，n,k。

第二行，n个数，分别表示多边形每条边的长度（按顺时针次序依次给出，即分别为AB,BC,CD,DE……的长度）。

以下k行，每行两个字母和一个数，两个字母表示该连线的起止点，数字表示长度。

最后一行，两个字母，分别为他跑步的起点和终点。

所有的一行的字母、数字之间用一个空格隔开。

输出格式：

输出文件为run.out。

一行，一个数，表示最短路的长度。

输入输出样例

输入样例#1： 复制

5 2
6 4 5 4 2
A D 7
E B 8
A D

输出样例#1： 复制

6

说明

对于20%的数据，k=0；

对于50%的数据，k≤10；

对于100%的数据，1≤n≤20，0≤m≤50，k≤100，所有路径长度均不大于1000。

思路：这是我第一次跪在scanf上，用scanf输入竟然会RE简直不可思议。floyed最短路即可。

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define MAXN 30
using namespace std;
int n,k;
int map[MAXN][MAXN];
int main(){
    memset(map,0x3f,sizeof(map));
    scanf("%d%d",&n,&k);
    for(int i=;i<=n;i++){
        int x;
        scanf("%d",&x);
        map[i][i%n+]=map[i%n+][i]=x;
    }
    for(int i=;i<=k;i++){
        char a,b;int x;
        cin>>a>>b>>x;
        if(map[a-'A'+][b-'A'+]<)    map[a-'A'+][b-'A'+]=map[b-'A'+][a-'A'+]=max(map[a-'A'+][b-'A'+],x);
        else map[a-'A'+][b-'A'+]=map[b-'A'+][a-'A'+]=x;
    }
    for(int i=;i<=n;i++)
        if(map[i][i]>)    map[i][i]=;
    for(int k=;k<=n;k++)
        for(int i=;i<=n;i++)
            for(int j=;j<=n;j++)
                if(i!=j&&i!=k&&j!=k&&map[i][j]>map[i][k]+map[k][j])
                    map[j][i]=map[i][j]=map[i][k]+map[k][j];
    char a,b;
    cin>>a>>b;
    cout<<map[a-'A'+][b-'A'+];
}