codeforces 571B--Minimization（贪心+dp）

D. Minimization

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You've got array A, consisting of n integers
and a positive integer k. Array A is
indexed by integers from 1 to n.

You need to permute the array elements so that value

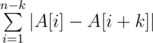
became minimal possible. In particular, it is allowed not to change order of elements at all.

Input

The first line contains two integers n, k (2 ≤ n ≤ 3·105, 1 ≤ k ≤ min(5000, n - 1)).

The second line contains n integers A[1], A[2], ..., A[n] ( - 109 ≤ A[i] ≤ 109),
separate by spaces — elements of the array A.

Output

Print the minimum possible value of the sum described in the statement.

Sample test(s)

input

3 2
1 2 4

output

1

input

5 2
3 -5 3 -5 3

output

0

input

6 3
4 3 4 3 2 5

output

3

Note

In the first test one of the optimal permutations is 1 4 2.

In the second test the initial order is optimal.

In the third test one of the optimal permutations is 2 3 4 4 3 5.

题目链接：点击打开链接

题目大意：给出n个数。给出一个k值。问n个数要怎么排列能够使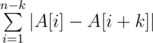的值最小。

首先我们能够想到，一段连续的数在a[i],a[i+k],a[i+2*k]，。，那么对于这些数来说他们的差的和是最小的。

所以先对n个数排序。然后将这n个数分成k段，k段中有k-n%k段的长度是n/k。n%k段的长度是n/k+1，这些段刚好能够填满n个数的序列，这n个数的总的差是a[n]-a[1]，当中有k-1个断点。是不会被统计到的，所以问题就转化成了怎样分开序列，使得分成要求的段的个数和段的长度，并且使断点的和最大，这样就会保证终于的结果最小。

dp[i][j]从头開始分出了i段成都为n/k的。j段n/k+1的断点的最大值。那么状态转移方程：

dp[i][j] = max(dp[i][j],dp[i-1][j]+a[k+1]-a[k]) ;

dp[i][j] = max(dp[i][j],dp[i][j-1]+a[k+1]-a[k]) ;

终于a[n]-a[1]-dp[num0][num1]

注意当k大于n的时候，结果是0

#include <cstdio>
#include <cstring>
#include <stack>
#include <algorithm>
using namespace std ;
#define LL __int64
LL a[300100] , sum[300100];
LL dp[5010][5010] ;
int main() {
    int n , k , i , j , l0 , l1 , num1 , num0 ;
    LL max1 ;
    while( scanf("%d %d", &n, &k) != EOF ) {
        sum[0] = 0 ;
        for(i = 1 ; i <= n ; i++) {
            scanf("%I64d", &a[i]) ;
            sum[i] = a[i] + sum[i-1] ;
        }
        sort(a+1,a+n+1) ;
        if( n <= k ) {
            printf("0\n") ;
            continue ;
        }
        memset(dp,0,sizeof(dp)) ;
        l0 = n/k ;
        l1 = n/k+1 ;
        num0 = k-n%k ;
        num1 = n%k ;
        a[0] = a[1] ;
        for(i = 0 ; i <= num0 ; i++) {
            for(j = 0 ; j <= num1 ; j++) {
                if( i == 0 && j == 0 ) continue ;
                if( i ) {
                    k = (i-1)*l0 + j*l1 ;
                    dp[i][j] = max(dp[i][j],dp[i-1][j]+a[k+1]-a[k]) ;
                }
                if( j ) {
                    k = i*l0 + (j-1)*l1 ;
                    dp[i][j] = max(dp[i][j],dp[i][j-1]+a[k+1]-a[k]) ;
                }
            }
        }
        printf("%I64d\n", a[n]-a[1]-dp[num0][num1]) ;

    }
    return 0 ;
}