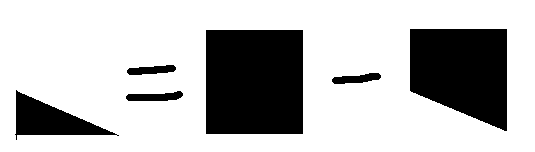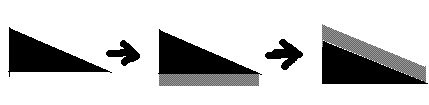POJ 2008
这道题,说实话,细节很多。不过,我没想到,光细节就能搞死人了。。。
参考了http://www.cppblog.com/varg-vikernes/archive/2010/03/12/109559.html
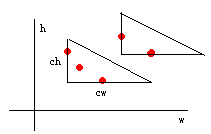
首先,要把所有牛放到坐标系上来表示。目的,就是求出包含最多点的直角三角形。
直角三角形的两条直角边上都必须有点,也就是一组牛中的具有最小height的点和具有最小width的点。
直角三角形的边长也是固定的,cw = C/B,ch = C/A。这个还好说,从那个限制条件可以推出来的。初中都学过,呵呵。
Step1:求出经过一个点的所有可能存在的三角形。
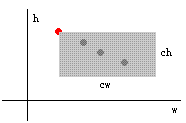
其实也就是在该点下方的灰色区域中选择点来确定一个三角形。
Step2:求出经过一个点的所有可能存在的三角形中,最多包含的点数。
解法相当精妙。
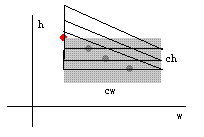
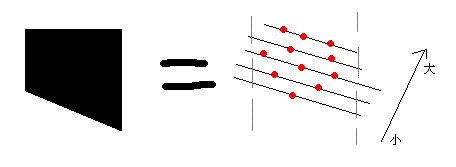
求一个三角形内的点数,可以分解为一个矩形内的点数减去一个梯形内的点数。
用这个方法,求出最上面那个三角形的点数之后。可以继续递推得到下面其他三角形的点数。
也就是加上一个矩形,再减去一个梯形。
如果点按照高度排序以后,那么后面矩形里的点一定是后出现的。这样就可以做到随时增加矩形。
但是减去梯形这个操作,就难理解一点,把点按照A*H + B*W来排序,就能保证后面梯形里的点一定是后出现的。
可见,A*H + B*W 值的大小决定了他们的位置分布。完全可以保证这个顺序。
这种数形结合的方法实在是相当精妙!
在退出点的时候,我选择用优先队列来做。写得很锉
#include <cstdio>
#include <iostream>
#include <cstring>
#include <cctype>
#include <vector>
#include <queue>
#include <algorithm>
#define LL unsigned __int64
#pragma comment(linker, "/STACK:1024000000,1024000000")
using namespace std; const int N=; struct Node{
int x,y;
int AH;
bool operator <(const Node &a) const {
if(y>a.y) return true;
else if(y==a.y){
if(x<a.x) return true;
}
return false;
}
}node[N];
int n,A,B,C,xh,yh;
struct Int_Node{
int AH;
Int_Node(int x){AH=x;};
bool operator<(const Int_Node &a)const {
if(AH<a.AH) return true;
return false;
}
};
priority_queue<Int_Node>Q; int main(){
int ah,ans=;
while(scanf("%d",&n)!=EOF){
ans=;
scanf("%d%d%d",&A,&B,&C);
yh=C/B; xh=C/A;
for(int i=;i<n;i++){
scanf("%d%d",&node[i].x,&node[i].y);
node[i].AH=A*node[i].x+B*node[i].y;
}
sort(node,node+n);
for(int i=;i<n;i++){
int xmin=node[i].x,ymin=node[i].y;
ah=A*xmin+B*ymin;
int j;
for(j=;j<i;j++){
if(node[j].y==ymin) break;
if(node[j].x<=xmin+xh&&node[j].y<=ymin+yh&&node[j].x>=xmin)
if(A*node[j].x+B*node[j].y-ah<=C)
Q.push(Int_Node(node[j].AH));
}
for(j;j<n&&node[j].x<=xmin+xh&&node[j].y==ymin&&node[j].x>=xmin;j++)
Q.push(Int_Node(node[j].AH));
int ts=Q.size();
ans=max(ans,ts);
for(int k=j;node[k].y+yh>=node[i].y&&k<n;k++){
if(node[k].y<ymin){
ymin=node[k].y;
ah=A*xmin+B*ymin;
int p;
for(p=k;node[p].y==ymin&&p<n;p++){
if(node[p].x<=xmin+xh&&node[p].x>=xmin){
Q.push(Int_Node(node[p].AH));
}
}
k=p-;int tmp;
while(!Q.empty()){
tmp=Q.top().AH;
if(tmp-ah>C){
Q.pop();
}
else
break;
}
ts=Q.size();
ans=max(ans,ts);
}
}
while(!Q.empty())
Q.pop();
}
printf("%d\n",ans);
}
return ;
}
POJ 2008的更多相关文章
- POJ 1511 Invitation Cards / UVA 721 Invitation Cards / SPOJ Invitation / UVAlive Invitation Cards / SCU 1132 Invitation Cards / ZOJ 2008 Invitation Cards / HDU 1535 (图论,最短路径)
POJ 1511 Invitation Cards / UVA 721 Invitation Cards / SPOJ Invitation / UVAlive Invitation Cards / ...
- HDU 2494/POJ 3930 Elevator(模拟)(2008 Asia Regional Beijing)
Description Too worrying about the house price bubble, poor Mike sold his house and rent an apartmen ...
- POJ 1511 Invitation Cards (ZOJ 2008) 使用优先队列的dijkstra
传送门: http://poj.org/problem?id=1511 http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=1008 ...
- POJ 3608 Bridge Across Islands --凸包间距离,旋转卡壳
题意: 给你两个凸包,求其最短距离. 解法: POJ 我真的是弄不懂了,也不说一声点就是按顺时针给出的,不用调整点顺序. 还是说数据水了,没出乱给点或给逆时针点的数据呢..我直接默认顺时针给的点居然A ...
- POJ 3322(广搜)
---恢复内容开始--- http://poj.org/problem?id=3322 题意:http://jandan.net/2008/01/24/bloxorz.html就是这个鬼游戏 我也是郁 ...
- (转)POJ题目分类
初期:一.基本算法: (1)枚举. (poj1753,poj2965) (2)贪心(poj1328,poj2109,poj2586) (3)递归和分治法. (4)递推. ...
- poj分类
初期: 一.基本算法: (1)枚举. (poj1753,poj2965) (2)贪心(poj1328,poj2109,poj2586) (3)递归和分治法. ( ...
- [双连通分量] POJ 3694 Network
Network Time Limit: 5000MS Memory Limit: 65536K Total Submissions: 9434 Accepted: 3511 Descripti ...
- Poj(3686),最小权匹配,多重匹配,KM
题目链接 The Windy's | Time Limit: 5000MS | Memory Limit: 65536K | | Total Submissions: 4939 | Accepted: ...
随机推荐
- Java 发送短信
这是一个调用sms接口发短信的程序,支持同时发送的短信量并不是很大,只作为学习使用(当然如果你想内部使用也行) 源码:package com; import org.apache.commons.ht ...
- 0507-php独立环境的安装与配置
1.在一个纯英文目录下新建三个文件夹 2.安装apache(选择好版本) 过程中该填的按格式填好,其余的只更改安装目录即可 如果报错1901是安装版本的问题. 检查:安装完成后localhost打开为 ...
- hdu3507Print Article(斜率优化dp)
Print Article Time Limit: 9000/3000 MS (Java/Others) Memory Limit: 131072/65536 K (Java/Others)To ...
- android切换卡顿解决方法
如果想要让应用用户流畅的滑动体验的话,那么就必须对activity和fragment的生命周期有一个完整的概念以及在何种情况下会触发哪些事件. 在自己目前做的项目中,就遇到了这样的问题,那么就把自己的 ...
- Flutter GitLab 客户端
F4Lab Flutter for GitLab. 欢迎参加一起完成
- 2013款MacBook Air装Windows7单系统
经过两天的摸索,查找无数资料终于把2013款的MacBook Air装上了WIN 7,虽然网上有很多的资料但是都不是我想要的,第一个我的是2013款的MacBook Air,跟原来2012 11款Ma ...
- hadoop job history server
默认情况下是没有启动的,需要配置完后手工启动服务. 1. 修改mapred-site.xml,添加如下内容(cluster mode, RM) <property> <nam ...
- 《计算机图形学基础(OpenGL版)》勘误表
第1版第1次印刷: 所在页码 所在行 原内容 更正为 41 16 k=Δx/Δy k=Δy/Δx 46 6 s-t=2Δy/Δx(xi+1)+2b+2yi-1 s-t=2Δy/Δx(xi+1)+2b- ...
- icheck使用
1.使用: <link rel="stylesheet" href="css/skins/all.css">或者<link rel=" ...
- Spark中Task,Partition,RDD、节点数、Executor数、core数目的关系和Application,Driver,Job,Task,Stage理解
梳理一下Spark中关于并发度涉及的几个概念File,Block,Split,Task,Partition,RDD以及节点数.Executor数.core数目的关系. 输入可能以多个文件的形式存储在H ...