Kotlin实现LeetCode算法题之Median of Two Sorted Arrays

题目Median of Two Sorted Arrays（难度Hard）

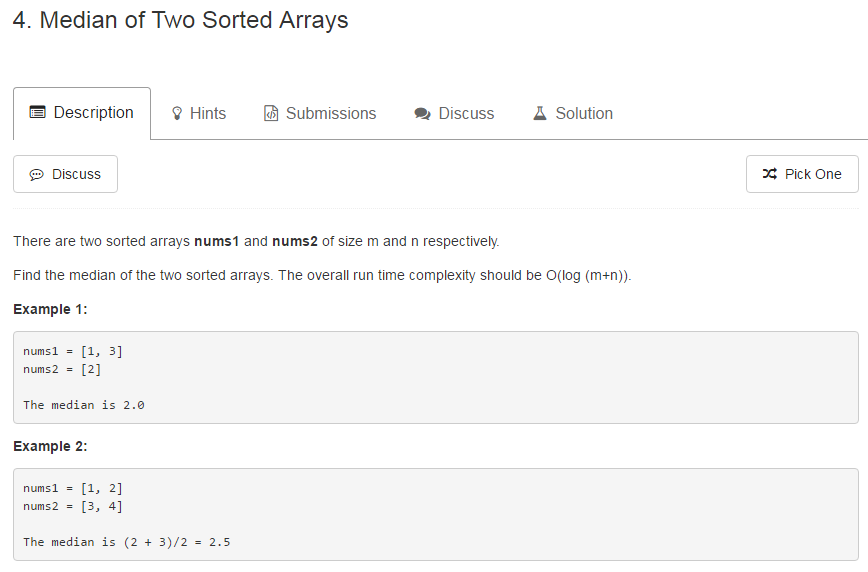
方案1，数组合并&排序调用Java方法

 import java.util.*

 class Solution {
     fun findMedianSortedArrays(nums1: IntArray, nums2: IntArray): Double {
         val lenNums1 = nums1.size
         val lenNums2 = nums2.size

         val array = Arrays.copyOf(nums1, lenNums1 + lenNums2)
         System.arraycopy(nums2, , array, lenNums1, lenNums2)

         Arrays.sort(array)

         var median: Double
         val lenArray = array.size
          == ) {
             median = array[(lenArray - ) / ].toDouble()
         } else {
             median = (array[(lenArray - ) / ] + array[lenArray / ]).toDouble() /
         }

         return median
     }
 }

提交详情1

平均耗时0.25ms。

方案2，数组合并&排序调用Kotlin方法

 class Solution {
     fun findMedianSortedArrays(nums1: IntArray, nums2: IntArray): Double {
         val lenNums1 = nums1.size
         val lenNums2 = nums2.size

         val array = IntArray(lenNums1 + lenNums2)
         System.arraycopy(nums1, , array, , lenNums1)
         System.arraycopy(nums2, , array, lenNums1, lenNums2)

         array.sort()

         var median: Double
         val lenArray = array.size
          == ) {
             median = array[(lenArray - ) / ].toDouble()
         } else {
             median = (array[(lenArray - ) / ] + array[lenArray / ]).toDouble() /
         }

         return median
     }
 }

提交详情2

平均耗时0.27ms。

Java & Kotlin代码对比

其实，通过源码可以发现，方案1和2在对数组进行合并与排序时调用的方法是一样的。

Arrays.java

 public static int[] copyOf(int[] original, int newLength) {
     int[] copy = new int[newLength];
     System.arraycopy(original, , copy, ,
                      Math.min(original.length, newLength));
     return copy;
 }

copyOf方法内部调用的还是System的静态方法arraycopy（native就不往下追了）。

System.java

 public static native void arraycopy(Object src,  int  srcPos,
                                         Object dest, int destPos,
                                         int length);

Arrays.kt

 /**
  * Creates a new array of the specified [size], where each element is calculated by calling the specified
  * [init] function. The [init] function returns an array element given its index.
  */
 public inline constructor(size: Int, init: (Int) -> Int)

IntArray(size: Int)会生成一个大小为size，元素值由init方法利用下标值计算而来，如果init不传入，那么默认均为0。

Arrays.kt

 public fun IntArray.sort(): Unit {
     ) java.util.Arrays.sort(this)
 }

Kotlin中IntArray的扩展方法sort，内部调用的是Java中Arrays的sort方法。

Arrays.java

 public static void sort(int[] a) {
     DualPivotQuicksort.sort(a, , a.length - , , );
 }

Arrays的sort方法最终是通过快排来实现的。而快速排序的时间复杂度为O(nlog(n))，但是题目要求量级为O(log(m+n))。

方案3，分治法求中位数

 class Solution {
     fun findMedianSortedArrays(nums1: IntArray, nums2: IntArray): Double {
         var media1: Int

         val len1 = nums1.size
         val len2 = nums2.size

          == ) {
             media1 = getMedian(nums1, nums2, , len1 - , , len2 - , (len1 + len2) /  + )
             return media1 / 1.0
         } else {
             media1 = getMedian(nums1, nums2, , len1 - , , len2 - , (len1 + len2) / )
             media2 = getMedian(nums1, nums2, , len1 - , , len2 - , (len1 + len2) /  + )
             return (media1 + media2) / 2.0
         }
     }

     fun getMedian(nums1: IntArray, nums2: IntArray, s1: Int, n1: Int, s2: Int, n2: Int, k: Int): Int {
         val x = (s1 + n1) /
         val y = (s2 + n2) / 

         if (s1 > n1)
             ]

         if (s2 > n2)
             ]

         return if (nums1[x] <= nums2[y]) {
             ) {
                 getMedian(nums1, nums2, s1, n1, s2, y - , k)
             } else {
                 getMedian(nums1, nums2, x + , n1, s2, n2, k - (x - s1) - )
             }
         } else {
             ) {
                 getMedian(nums1, nums2, s1, x - , s2, n2, k)
             } else {
                 getMedian(nums1, nums2, s1, n1, y + , n2, k - (y - s2) - )
             }
         }
     }
 }

提交详情3

平均耗时0.32ms。

结果分析

但从LeetCode的测试用例所消耗的时间来看，上述三种方案没有明显的区别，理论上分治法的时间复杂度为O(log(n))。