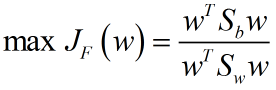拉普拉斯矩阵(Laplace Matrix)与瑞利熵(Rayleigh quotient)
作者:桂。
时间:2017-04-13 07:43:03
链接:http://www.cnblogs.com/xingshansi/p/6702188.html
声明:欢迎被转载,不过记得注明出处哦~

前言
前面分析了非负矩阵分解(NMF)的应用,总觉得NMF与谱聚类(Spectral clustering)的思想很相似,打算分析对比一下。谱聚类更像是基于图(Graph)的思想,其中涉及到一个重要概念就是拉普拉斯矩阵(Laplace matrix),想着先梳理一下这个矩阵:
1)拉普拉斯矩阵基本定义
2)拉普拉斯矩阵意义及性质
3)瑞利熵(Rayleigh quotient)
内容为自己的学习记录,很多地方都借鉴了别人,最后一并给出链接。
一、拉普拉斯矩阵基本定义
对于图G,一般用点的集合V和边的集合E来描述:G(V,E)。现在有这样一个图,如何定义拉普拉斯矩阵呢?这里涉及到两个常用矩阵:邻接矩阵、度矩阵。
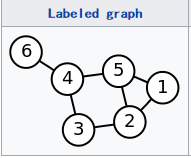
从最简单的应用入手,不同数据点相通权重为1,不相通权重为0.
首先求解邻接矩阵W:

将每一列求和,这个数值的对角形式对应就是度矩阵D:
$d_i = \sum\limits_{j=1}^{n}w_{ij}$
写成矩阵形式:
$\mathbf{D} = \left( \begin{array}{ccc} d_1 & \ldots & \ldots \\ \ldots & d_2 & \ldots \\ \vdots & \vdots & \ddots \\ \ldots & \ldots & d_n \end{array} \right)$

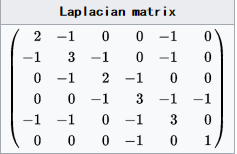
从而得到拉普拉斯矩阵L的定义:
$L= D-W$
二、拉普拉斯矩阵意义及性质
不失一般性,$v_i$与$v_j$的权重不再是1而是$w_{ij}$,$f(v_i)$表示节点$v_i$的函数,对应实际应用它可以是一个概率值、一个像素值等等。
对任意向量$f$,
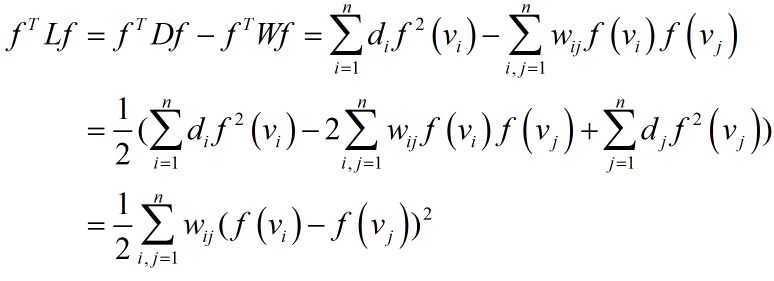
这样一来,拉普拉斯矩阵的意义就比较明显了,它是一种基于欧式距离的测度,如果$w_{ij} = 1$,上式对应就是多有数据点的距离之和,同时也可以看出:D对应二次项,W对应不同一次项相乘。拉普拉斯矩阵是半正定的,且对应的n个实数特征值都大于等于0,即:$0 =\lambda_1 \leq \lambda_2 \leq... \leq \lambda_n$。
三、瑞利熵
提到拉普拉斯矩阵,就不能不提瑞利熵。
A-普通瑞利熵
给出定义:
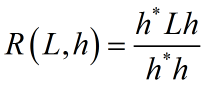
因为对h幅值进行条件,不会影响R的取值,同时也不会改变h向量的方向,对于一般优化问题(以max为例,其他类似):
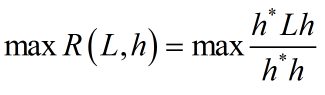
可以转化为拉格朗日乘子问题:

c为常数,即:
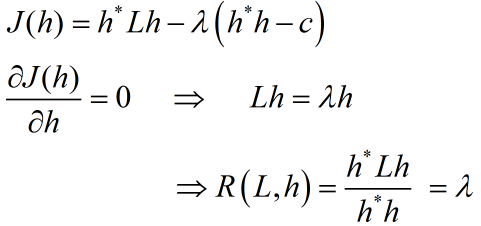
可以看出:
- R的最大值就是L最大特征值,R的最小值就是L最小特征值
- h的解,就是L对应的特征向量
是不是很熟悉啊?
- 简单回顾一下主成分分析(PCA)算法:
设p为矩阵A的单位投影矩阵,最大化投影结果:
PCA就是瑞利熵理论的一个应用。
后面分析谱聚类(Spectral clustering),其中RatioCut算法也是瑞利熵的一个应用。
B-泛化瑞利熵
为什么叫泛化呢?对于
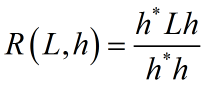
可以看到分子是一般形式,而分母是${{h^*}Dh}$在D取单位阵时的特殊情况,将其一般化:
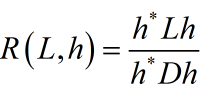
同理可以得到:

适当变形:
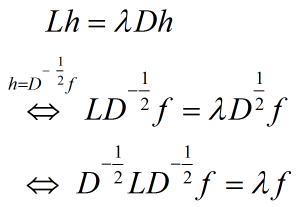
这个时候表达式就是:
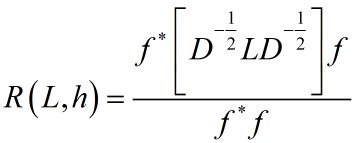
又回到了普通瑞利熵问题,求解就方便了。
- 简单回顾一下Fisher线性判别分析(Linear discriminant analysis, LDA)算法:
Fisher判别准则函数:
分子分母分别是类内、类间距离。这个准则函数就是泛化瑞利熵的形式。
LDA是泛化瑞利熵的一个应用。
后面分析谱聚类(Spectral clustering),其中NCut算法也是泛化瑞利熵的一个应用。
参考:
瑞利熵:https://en.wikipedia.org/wiki/Rayleigh_quotient
拉普拉斯矩阵:http://www.cnblogs.com/pinard/p/6221564.html
拉普拉斯矩阵(Laplace Matrix)与瑞利熵(Rayleigh quotient)的更多相关文章
- 拉普拉斯矩阵(Laplacian Matrix) 及半正定性证明
摘自 https://blog.csdn.net/beiyangdashu/article/details/49300479 和 https://en.wikipedia.org/wiki/Lapla ...
- SC3聚类 | 拉普拉斯矩阵 | Laplacian matrix | 图论 | R代码
Laplacian和PCA貌似是同一种性质的方法,坐标系变换.只是拉普拉斯属于图论的范畴,术语更加专业了. 要看就把一篇文章看完整,再看其中有什么值得借鉴的,总结归纳理解后的东西才是属于你的. 问题: ...
- 拉普拉斯矩阵(Laplacian matrix)
原文地址:https://www.jianshu.com/p/f864bac6cb7a 拉普拉斯矩阵是图论中用到的一种重要矩阵,给定一个有n个顶点的图 G=(V,E),其拉普拉斯矩阵被定义为 L = ...
- graph Laplacian 拉普拉斯矩阵
转自:https://www.kechuang.org/t/84022?page=0&highlight=859356,感谢分享! 在机器学习.多维信号处理等领域,凡涉及到图论的地方,相信小伙 ...
- R语言编程艺术# 矩阵(matrix)和数组(array)
矩阵(matrix)是一种特殊的向量,包含两个附加的属性:行数和列数.所以矩阵也是和向量一样,有模式(数据类型)的概念.(但反过来,向量却不能看作是只有一列或一行的矩阵. 数组(array)是R里更一 ...
- 【Math for ML】矩阵分解(Matrix Decompositions) (下)
[Math for ML]矩阵分解(Matrix Decompositions) (上) I. 奇异值分解(Singular Value Decomposition) 1. 定义 Singular V ...
- 【Math for ML】矩阵分解(Matrix Decompositions) (上)
I. 行列式(Determinants)和迹(Trace) 1. 行列式(Determinants) 为避免和绝对值符号混淆,本文一般使用\(det(A)\)来表示矩阵\(A\)的行列式.另外这里的\ ...
- R语言编程艺术#02#矩阵(matrix)和数组(array)
矩阵(matrix)是一种特殊的向量,包含两个附加的属性:行数和列数.所以矩阵也是和向量一样,有模式(数据类型)的概念.(但反过来,向量却不能看作是只有一列或一行的矩阵. 数组(array)是R里更一 ...
- NumPy 矩阵库(Matrix)
NumPy 矩阵库(Matrix) NumPy 中包含了一个矩阵库 numpy.matlib,该模块中的函数返回的是一个矩阵,而不是 ndarray 对象. 一个 的矩阵是一个由行(row)列(col ...
随机推荐
- python 写的几道题
''' #乘法口诀''' for i in range(1,10): for j in range(1,i+1): print("%d*%d=%2d" % (i,j,i*j),en ...
- YARN学习笔记(一)——YARN的简介
YARN的简介 什么是YARN MRv1的架构和缺陷 经典MapReduce的局限性 解决可伸缩性问题 YARN的架构 一个可运行任何分布式应用程序的集群 YARN中的应用程序提交 YARN的其他特性 ...
- Compare Version Numbers leetcode
Compare two version numbers version1 and version2.If version1 > version2 return 1, if version1 &l ...
- 简易漫画网站搭建-漫画喵Server版
小喵的唠叨话:寒假的时候写了一个漫画爬虫,爬取了好几个漫画,不过一直没有找到合适的漫画阅读的工具.因此最近就试着自己写一个漫画的网站,放在公网上或者局域网里,这样就能随时随地用手机.Pad看漫画了. ...
- 关于Maven的安装及初步使用
关于Maven的初步使用 1. 下载: 进入http://maven.apache.org/download.cgi下载 Maven 3.3.1 2. 将压缩包解压到自己的硬盘中,最好放在某个盘 ...
- hdoj 1175 (bfs)
题意: 判断两点之间是否可以通过至多有两次转变方向以达到相连,就是平时玩的连连看游戏,但是不能从外面绕过去. 思路:bfs,给每个加入的队列的点添加转变方向次数turn和点当前要走的方向dir属性,起 ...
- Unity中溶解shader的总结
在实际的游戏工程中,经常美术和策划会提出溶解的表现要求.比如子弹在飞行的时候,弹道不断的消融:角色受到大型炮弹的攻击,在击飞的时候不断的消融等等诸如此类的表现.一般的消融都是结合粒子系统来实现,通过给 ...
- javascript 随机显示指定内容
今天碰到一个需求,一个页面显示赞助厂商的信息,但是厂商要求排序要随机排,因为是个静态页面不是读取数据库的,所以打算用js来控制 var arr = new Array('张三', '李四', '王五' ...
- Linux关机重启指令
关机: init 0 [使用Linux的运行级别] halt poweroff shutdown -h [系统会发出广播信息,显示即将关机时间] shutdown -c [取消关机计划] 重启: r ...
- [译]Selenium Python文档:一、安装
1.1.简介 Selenium Python为使用Selenium WebDriver来编写功能/验证测试提供了一个简单的API接口.通过Selenium Python API,你可以以一种非常直观的 ...