信息论之从熵、惊奇到交叉熵、KL散度和互信息
一、熵(PRML)
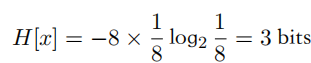
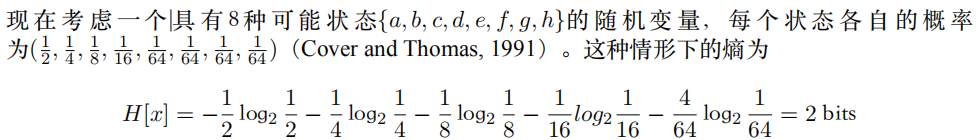
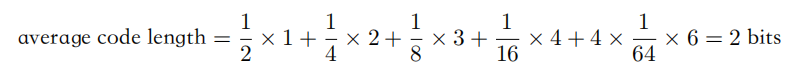
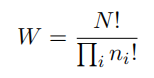
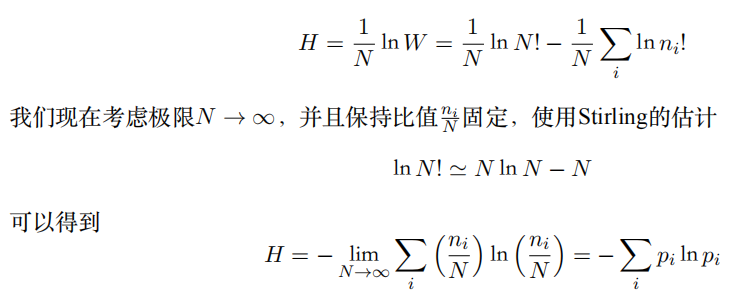
二、惊奇与信息

- 如果有⼈告诉我们⼀个相当不可能的事件发⽣了,我们收到的信息要多于我们被告知某个很可能发⽣的事件发⽣时收到的信息。
- 如果听到⼀个必然事情,那么就不会接收到信息。EX: 明天有24h
- 如果有两个不相关的事件x和y,那么观察到两个事件同时发⽣时获得的信息应该等于观察到事件各⾃发⽣时获得的信息之和,即h(x, y) = h(x) + h(y)。
- 两个不相关事件是统计独⽴的,因此p(x, y) = p(x)p(y)。
- 其中,负号确保了信息⼀定是正数或者是零。
- 注意,低概率事件x对应于⾼的信息量。
- 对数的底遵循信息论使⽤2作为对数的底(2进制编码最短)。


三、熵的相关变量
熵用于衡量不确定性,其相当于是编码一个随机变量的平均最小编码长度(最优编码的下界,即huffman编码)
1.自信息-二进制编码长度
\]
2.信息熵
= - \int p(x)\ln p(x)dx
\\ = \int p(x)\ln \frac{1}{p(x)}dx
= \mathbb{E}_{x\sim p(x)}\left[\ln\frac{1}{p(x)}\right]
\]
3.交叉熵,用一个分布p(x)的编码去编码另一个分布q(x)的代价(平均编码长度)
= - \int p(x)\ln q(x)dx
\\ = \mathbb{E}_{x\sim p(x)}\left[\ln\frac{1}{q(x)}\right]
\]
分布q(x)的自信息(最小编码长度)关于分布p(x)的期望
Ex: q(x1) = 0.25需要2bits,例如00来编码,但p(x1)=0.01
,相当于用更短的编码来编码低频取值(不符合高频短码),可能导致编码代价更大。
随机变量取值越多,熵越大(信息增益)
4.KL散度,衡量两个分布p(x)和q(x)的距离(不相似程度):
用一个分布p(x)的编码去编码另一个分布q(x)的额外代价
若KL散度为0,则表示编码额外代价为0,即两个分布相同
= - \int p(x)\ln \frac{q(x)}{p(x)} dx
= \int p(x)\ln \frac{p(x)}{q(x)} dx
\\= \int p(x)\ln p(x) - p(x)\ln q(x)dx
\\ = - \int p(x)\ln q(x)dx - (-\int p(x)\ln p(x) )
\\ = C\Big(p(x)\Big\Vert q(x)\Big) - H\Big(p(x)\Big)
\\ =
\mathbb{E}_{x\sim p(x)}\left[\ln\frac{p(x)}{q(x)}\right] \]
由于熵为常数项,最小化交叉熵,相当于最小化KL散度(最大似然),离散形式即求和。
- 互信息

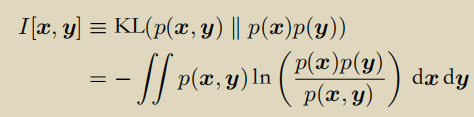
联合分布p(x, y)和边缘分布乘积累p(x)p(y)的KL散度。
如果互信息为0,则两个边缘分布独立p(x, y) = p(x) p(y)
信息论之从熵、惊奇到交叉熵、KL散度和互信息的更多相关文章
- 深度学习面试题07:sigmod交叉熵、softmax交叉熵
目录 sigmod交叉熵 Softmax转换 Softmax交叉熵 参考资料 sigmod交叉熵 Sigmod交叉熵实际就是我们所说的对数损失,它是针对二分类任务的损失函数,在神经网络中,一般输出层只 ...
- 信息论相关概念:熵 交叉熵 KL散度 JS散度
目录 机器学习基础--信息论相关概念总结以及理解 1. 信息量(熵) 2. KL散度 3. 交叉熵 4. JS散度 机器学习基础--信息论相关概念总结以及理解 摘要: 熵(entropy).KL 散度 ...
- 【机器学习基础】熵、KL散度、交叉熵
熵(entropy).KL 散度(Kullback-Leibler (KL) divergence)和交叉熵(cross-entropy)在机器学习的很多地方会用到.比如在决策树模型使用信息增益来选择 ...
- 交叉熵理解:softmax_cross_entropy,binary_cross_entropy,sigmoid_cross_entropy简介
cross entropy 交叉熵的概念网上一大堆了,具体问度娘,这里主要介绍深度学习中,使用交叉熵作为类别分类. 1.二元交叉熵 binary_cross_entropy 我们通常见的交叉熵是二元交 ...
- 第五节,损失函数:MSE和交叉熵
损失函数用于描述模型预测值与真实值的差距大小,一般有两种比较常见的算法——均值平方差(MSE)和交叉熵. 1.均值平方差(MSE):指参数估计值与参数真实值之差平方的期望值. 在神经网络计算时,预测值 ...
- 理解交叉熵(cross_entropy)作为损失函数在神经网络中的作用
交叉熵的作用 通过神经网络解决多分类问题时,最常用的一种方式就是在最后一层设置n个输出节点,无论在浅层神经网络还是在CNN中都是如此,比如,在AlexNet中最后的输出层有1000个节点: 而即便是R ...
- 信息论随笔3: 交叉熵与TF-IDF模型
接上文:信息论随笔2: 交叉熵.相对熵,及上上文:信息论随笔 在读<数学之美>的时候,相关性那一节对TF-IDF模型有这样一句描述:"其实 IDF 的概念就是一个特定条件下.关键 ...
- 最大似然估计 (Maximum Likelihood Estimation), 交叉熵 (Cross Entropy) 与深度神经网络
最近在看深度学习的"花书" (也就是Ian Goodfellow那本了),第五章机器学习基础部分的解释很精华,对比PRML少了很多复杂的推理,比较适合闲暇的时候翻开看看.今天准备写 ...
- 熵(Entropy),交叉熵(Cross-Entropy),KL-松散度(KL Divergence)
1.介绍: 当我们开发一个分类模型的时候,我们的目标是把输入映射到预测的概率上,当我们训练模型的时候就不停地调整参数使得我们预测出来的概率和真是的概率更加接近. 这篇文章我们关注在我们的模型假设这些类 ...
- 深度学习中交叉熵和KL散度和最大似然估计之间的关系
机器学习的面试题中经常会被问到交叉熵(cross entropy)和最大似然估计(MLE)或者KL散度有什么关系,查了一些资料发现优化这3个东西其实是等价的. 熵和交叉熵 提到交叉熵就需要了解下信息论 ...
随机推荐
- 08 分布式计算MapReduce--词频统计
def getText(): txt=open("D:\\test.txt","r").read() txt=txt.lower() punctuation = ...
- JAVA 在开发中如何选择集合实现类
先判断存储地类型(一组对象[单列]或者键值对[多列]) 一组对象:Collection接口 允许重复:list 增删多:LinkedList[底层维护了一个双向链表] 改查多;ArratList[底层 ...
- JAVA 学习打卡 day3
2022-04-25 22:53:16 1.运算符 表达式是由操作数与运算符所组成Java中的语句有很多种形式,表达式就是其中一种形式.表达式是由操作数与运算符所组成,操作数可以是常量.变量也可以是方 ...
- JAVA 学习打卡 day2
2022-04-23 16:43:32 1.字符类型 (1)字符和整型之间的相互转换 给字符变量赋值可以使用数值和字符,它们都可以使程序正确地运行.要注意的是,字符要用一对单引号('')括起 (2)常 ...
- java 在 map put方法是报 java.lang.NullPointerException的异常 处理办法
当在定义map变量时,如果没有初始化对象,那么默认map值为空的,此时对map进行操作,会报空指针异常,解决办法就是初始化map变量 或者,直接初始化变量,不用在代码块里面设置 Map<Stri ...
- 006Java程序运行机制
006Java程序运行机制 高级程序语言分为编译型和解释型两种,Java这两种特性都具备. 编译型还是解释型取决于翻译的时机. 以看一本外语书为例: 编译型:先把整本书翻译成中文版再看. 解释型:请个 ...
- Spring AOP的动态代理原理和XML与注解配置
AOP 实现底层就是对上面的动态代理的代码进行了封装,封装后我们只需要对需要关注的部分进行代码编写,并通过配置的方式完成指定目标的方法增强. 相关术语: Target(目标对象):代理的目标对象 Pr ...
- Mapper method 'org.lin.hms.dao.IndentDAO.insertIndent' has an unsupported return type: interface java.util.List
出现这种错误,说明sql语句执行成功,只是返回类型出了问题. 解决办法: mapper文件中的update,delete,insert语句是不需要设置返回类型的,它们都是默认返回一个int ,所以把返 ...
- [Lua]敏感字检测
参考链接: https://zhuanlan.zhihu.com/p/84685657 https://www.cnblogs.com/luguoshuai/p/9254190.html 一开始打算使 ...
- 【其他】etcd
配置 node1 name: etcd-1 data-dir: /data/etcd/node1 listen-client-urls: http://127.0.0.1:6701 advertise ...
