GIN--HOW POWERFUL GNN

HOW POWERFUL ARE GRAPH NEURAL NETWORKS?

本文是 Jure Leskovec 又一力作，首先对图神经网络的原理做了深入检出、提纲挈领的叙述，然后从原理方面介绍了如何发挥图神经网络的效用。

图神经网络可以分为三个阶段：

1. Aggregate：聚合邻居节点信息

   \[a^{(k)}_v = AGGREGATE^{(k)}(\{h_{\mu}^{(k−1)}:\mu\in N(v)\})
   \]

2. Combine：聚合邻居和当前节点

   \[h_{\mu}^{(k)} = COMBINE^{(k)}({h_{\mu}^{(k−1)},a^{(k)}_v})
   \]

3. Readout：整合表示图中所有节点

   \[h_G = READOUT(\{h^{(K)}_v|v \in G\})
   \]

在GraphSAGE中，Aggregate和Combine过程如下，GCN同理

那么如何衡量图神经网络是否学到了良好的表示，这里提到了 Weisfeiler-Lehman test ，有兴趣可以下去研究。

文章的和核心出发点在于：对于子树结构相同且对应节点特征相同的的俩个节点，一个有效的GNN应该有能力映射两个节点到embedding空间中相同的位置，决不会将两个不同的节点映射到同一embedding空间位置。

Intuitively, a maximally powerful GNN maps two nodes to the same location only if they have identical subtree structures with identical features on the corresponding nodes

A maximally powerful GNN would never map two different neighborhoods

因此，GNN的Aggregate必须是单射的，单射函数（一对一函数）如下

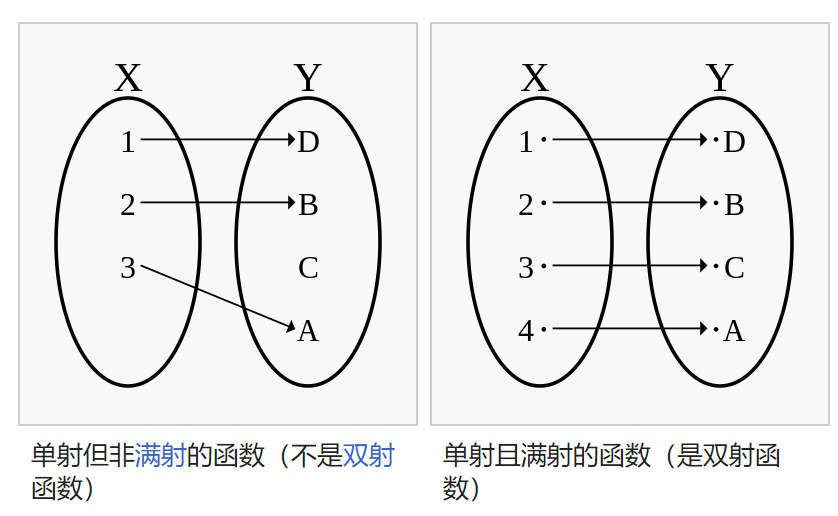
由此引出定理3，定理3是本文中一个重要的定理，其规定了一个powerful GNN的理论形式，即函数 \(f\) 的变量是一个multiset，Combine \(\phi\) 是单射函数， Readout 是单射函数。

那么如何根据定理3设计改进GNN？

GIN：Graph Isomorphism Network

针对节点分类任务，使用nodel-level级GIN：

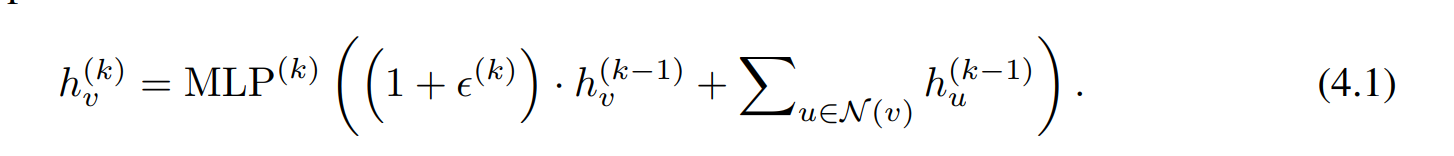
对于图分类任务，替换 \(h_G\) 如下

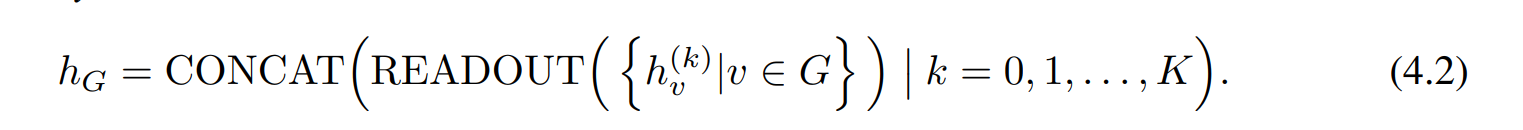
注意到式（4.1）做了两处改变，

• 使用sum作为agg函数
• 使用MLP替代 \(\sigma W\)

那么GIN是否有效？实验分别验证了 sum 和MLP 在此发挥的作用，分别用

(1) 1-layer perceptrons instead of MLPs and

(2) mean or max-pooling instead of the sum

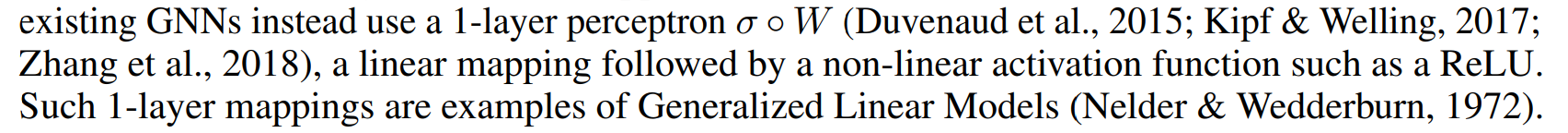
根据引理7，单层perceptrons更接近于线性映射，使GNN退化为简单的summing。

作者用下面两个图阐述了sum>mean>max，此部分内容有兴趣可以阅读原文。

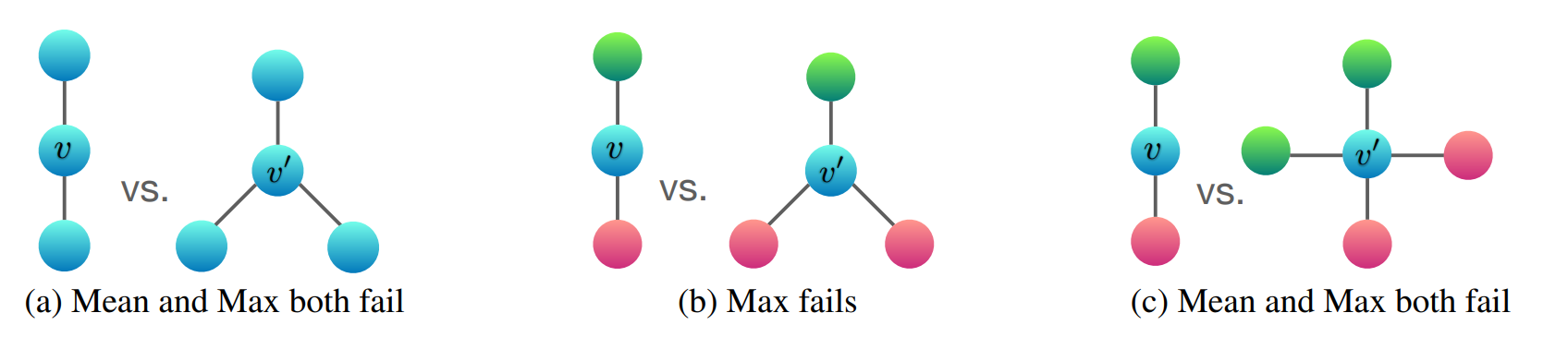
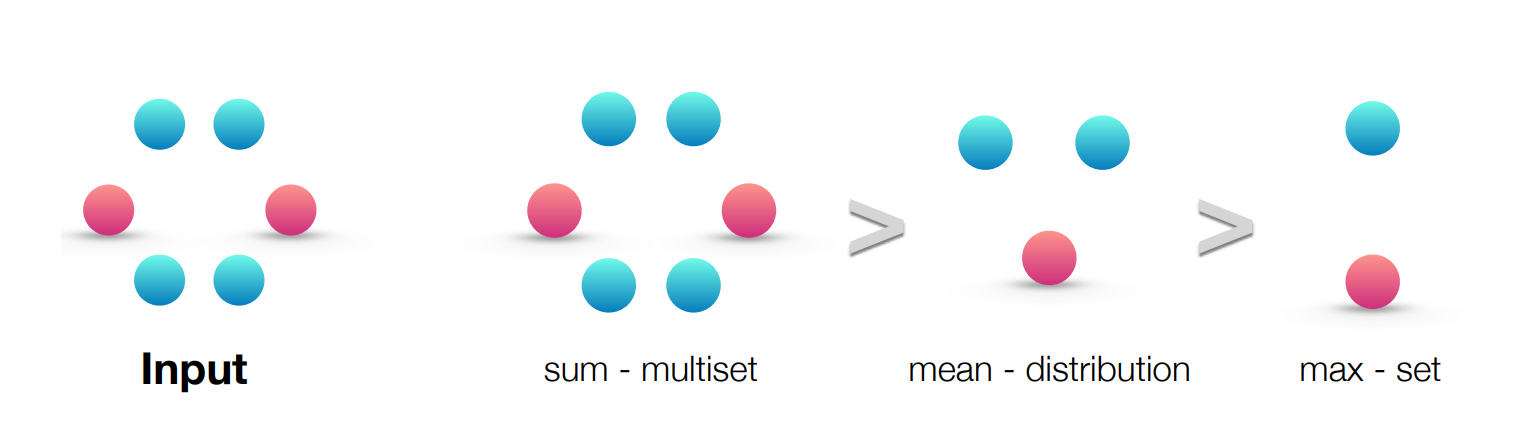
实验结果也验证了在大部分模型和任务上，GIN可以带来有效的提升。

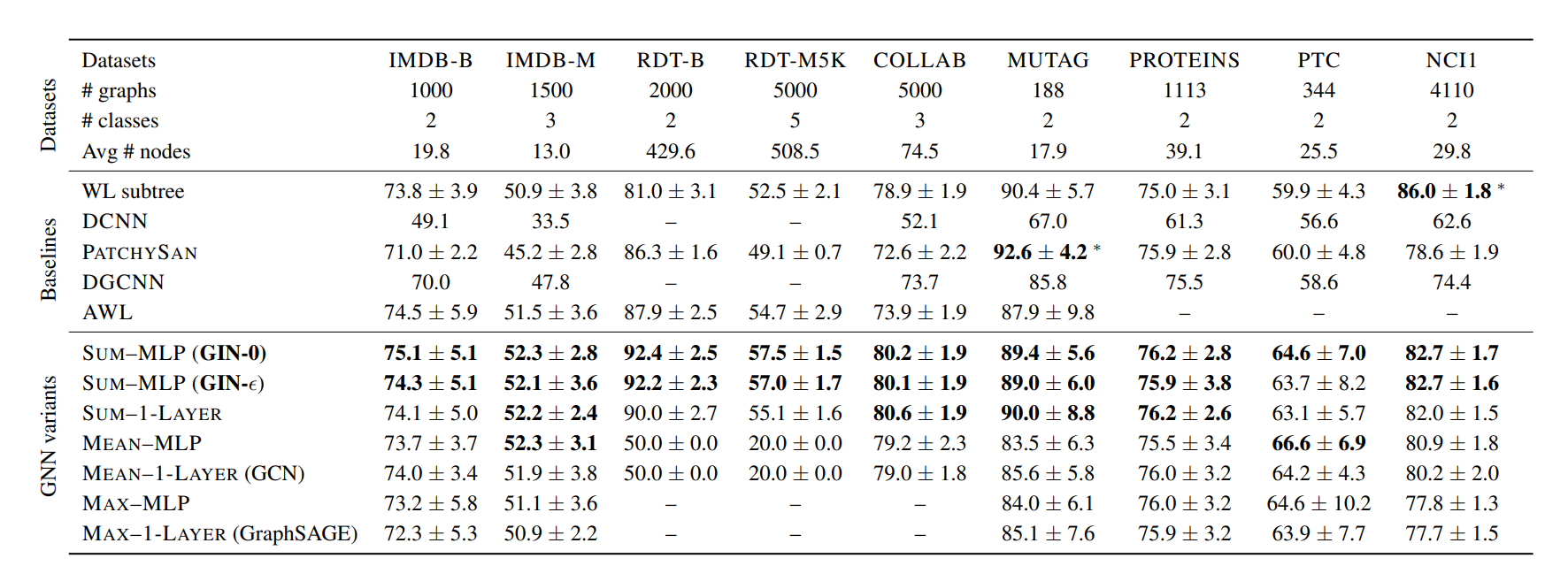
原文：HOW POWERFUL ARE GRAPH NEURAL NETWORKS?

官方GitHub：https://github.com/weihua916/powerful-gnns

《Graph Neural Networks多强大？》阅读笔记 - 陈乐天的文章 - 知乎 https://zhuanlan.zhihu.com/p/62006729

GraphSAGE: GCN落地必读论文 - 风浪的文章 - 知乎 https://zhuanlan.zhihu.com/p/62750137