题解 P2602 [ZJOI2010] 数字计数

虽然说是数位 dp 入门题但是还是不是很会（悲

看了题解才做出来，中途因为各种 SB 问题调了很长时间（悲

---

聪明的你一定能看出来这是数位 dp，因此令 \(i\) 为当前填的位数，\(limit\) 记录前 \(i - 1\) 位是否与边界相同，\(lead\) 记录前导零。

然后就是伟大的添维了，我们显然要记录目前统计的是哪个数字，然后我们还要记录这个数字出现的次数 \(sum\)。

这个时候 SX 这个天才会问了诶为什么要记录 \(sum\) 啊 \(sum\) 不就是答案吗这不就是脱了屁股放裤子吗？

其实这个我也没研究出个所以然来（悲），我只能说一点我自己浅显的理解，希望有巨佬能指出来我的错误，我的 QQ 是 2392303708 欢迎来喷并且指正 qwq。

首先我们当 \(i = 0\) 时肯定要返回的，返回什么值呢？返回 \(sum\)。我们是以记忆化搜索为框架，每个状态为一个节点会做出一棵树，以下面这张图为例，酱紫：

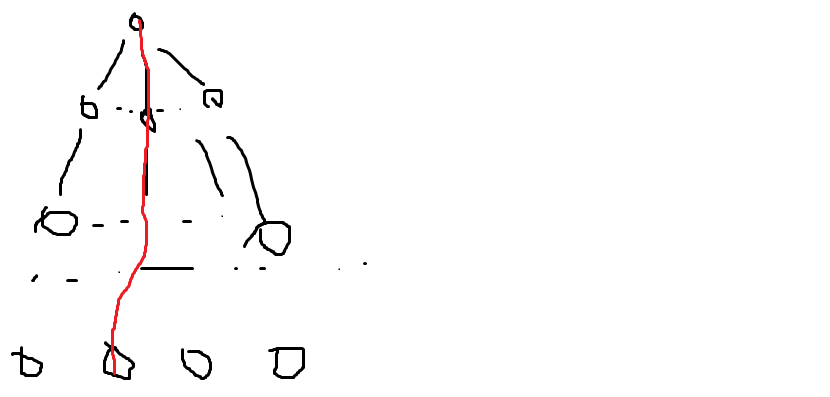
（反正是给自己看的图丑一点没关系）被红色标记过的链的末端的叶子节点的 \(sum\) 就是这条链上除了最后一个叶子节点要求数码出现次数（其实叶子节点没有数码的说，但是毕竟图都这么画了。。）。请注意我们返回 \(i = 0\) 的情况其实就是给 \(i = 1\) 的情况的，\(i = 1\) 的情况出现的数码次数显然是链上总和。

也就是说其实我们返回 \(i = 0\) 的情况就是给 \(i = 1\) 的状态做准备的┓( \´∀` )┏

因此我们要记录 \(sum\)，这样我们才能返回。

至于它要不要记录到状态里面捏。。。反正我开数组记录了，记了肯定没问题如果有不记录的方法 QQ 撅我（喜

//SIXIANG
#include <iostream>
#include <cstring>
#define MAXN 100000
#define int long long
#define QWQ cout << "QWQ" << endl;
using namespace std;
int f[20][114514][2][2], arr[20], tot = 0;
int digit(int i, int sum, int limit, int lead, int num) {
    if(!i) return sum;
    if(f[i][sum][limit][lead] != -1) return f[i][sum][limit][lead];
    int lim = ((limit) ? (arr[i]) : 9), rest = 0;
    for(int p = 0; p <= lim; p++)
        rest += digit(i - 1, sum + ((p || (!lead)) && (p == num)), (limit && (p == arr[i])), (lead && (!p)), num);
    f[i][sum][limit][lead] = rest;
    return rest;
}
int solve(int x, int num) {
    memset(f, -1, sizeof(f));
    memset(arr, 0, sizeof(arr));
    tot = 0;
    int tmp = x;
    do {
        arr[++tot] = x % 10;
        x /= 10;
    } while(x);
    return digit(tot, 0, 1, 1, num);
}
signed main() {
    int l, r; cin >> l >> r;
    for(int p = 0; p <= 9; p++) {
        cout << solve(r, p) - solve(l - 1, p) << ' ';
    }
}