发现Compound的第二个严重漏洞

本文转自 发现Compound的第二个严重漏洞 | 登链社区 | 深入浅出区块链技术 (learnblockchain.cn)

这个漏洞原作者在2022年02月23日已经发布过，由于内容比较敏感，发布后没多久就将违章的主要内容都删除了。然而，这个漏洞还是被利用了，March-15-2022 06:28:40 PM +8 UTC，Hundred Finance遭受攻击，黑客获利2363 ETH（价值超4000万美金）。Hundred Finance代码源自Compound，文中有在rinkeby上模拟攻击的交易，可以自行核对时间。

前置条件

1. 开通了多个代币的市场
2. 代币市场中有ERC777

利用过程

1. 攻击者在多个市场中存入资产，获得份额凭证。
2. 攻击者向ERC777的代币市场发起借款，并在借款转账时，触发事先准备好的回调，在回调中退出这个发生了借款的市场。
3. 攻击者赎回所有可以赎回的份额，由于借贷市场已经退出，因此不会在赎回时扣除用户的借款，因此可以正常退出，从而盗走借款。

攻击原理

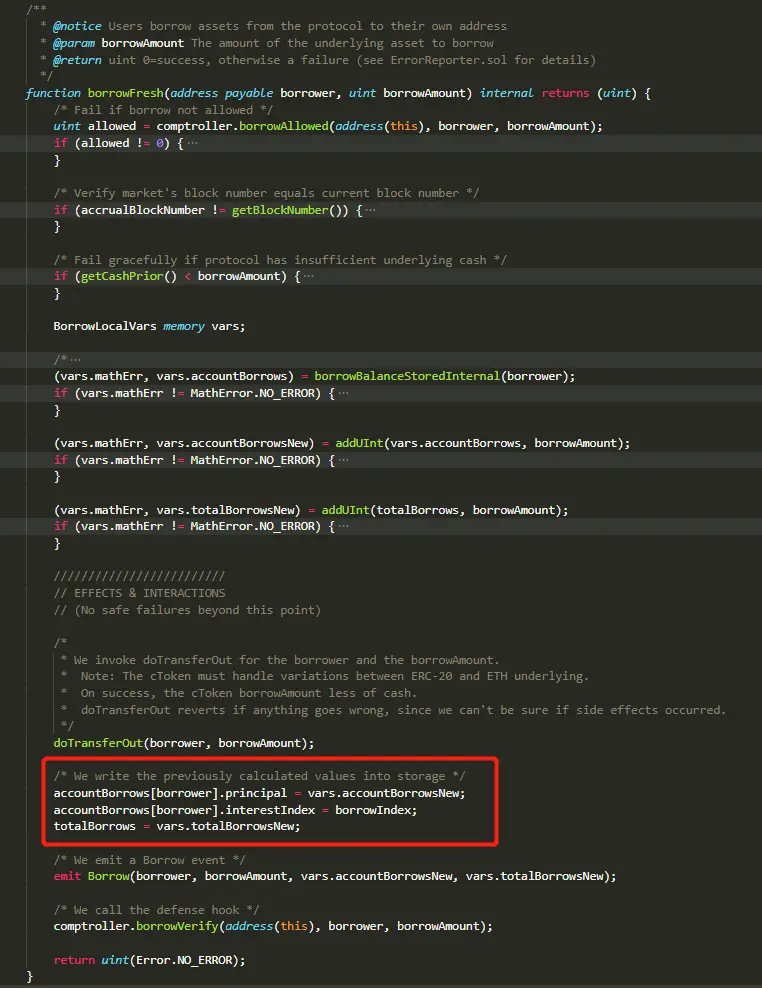
1. 在borrowFresh()函数中，在完成借款的各项检查和准备后，会给用户转账，并更新用户的借款账本。
2. 给用户转账doTransferOut()在更新用户账本之前，这使得用户可以有机会通过转账触发回调。
3. 攻击者在回调中可以调用comptroller的exitMarket()函数退出借款的市场，由于此时用户的借款账本还没有更新，因此exitMarket()中检查用户是否可以退出该市场的逻辑会验证通过，攻击者可以成功退出市场。
4. 攻击者退出借款市场后，再进行其他资产赎回时，由于发生借款的市场已经被退出，因此不会在赎回时计算这笔借款，从而可以成功赎回资产。
5. 通过上述方法，攻击者可以成功的将借款偷走。

相关代码

给借款人转账，然后更新用户账本
https://github.com/compound-finance/compound-protocol/blob/master/contracts/CToken.sol#L786

退出市场，检查用户是否可以退出

https://github.com/compound-finance/compound-protocol/blob/master/contracts/ComptrollerG7.sol#L175

以下是在rinkeby上模拟攻击的相关交易

https://rinkeby.etherscan.io/tx/0x944f46be4591dbed7d855e99b5707557fd074303ff9c1935b2bc35c5e61d2eda

可以看出，攻击合约按照前面描述的流程，完成攻击后，合约内的资产多了800USDT。

漏洞特性

根据上面的分析可知，只要代币市场中有ERC777存在，就具备了攻击的条件！
另外，有很多项目是fork自Compound的，如果在fork项目时，将转eth的代码改用当前应用较广泛的TransferHelper.safeTransferETH()，则会导致这种攻击的发生。因为TransferHelper.safeTransferETH()通常的实现没有限制gas。

总结

1. 使用重入锁并不能解决所有问题，可以考虑使用checks-effects-interactions模式，另外，转账最好放在一个完整逻辑的最开始或者最结尾，避免状态不一致。
2. 这个取名safeTransferETH()的函数，并不会给大家带来安全，相反留下了被攻击的可能。因此，应该慎用TransferHelper.safeTransferETH()方法，另外，也建议在safeTransferETH()的实现里面，将gas限制为5000，这样既可以解决往代理合约转账的问题，也会让攻击难以发生。