一步一步地完成题目——费解的开关（C/C++语言）递推、递归、顺序思维

前言

本文中博主将一步一步地、以正常人的顺序思维完成题目——费解的开关，使用的核心方法是递推与递归。

题目

参考题目：费解的开关

详细的题目信息相信大家都已经知道了，因此这里为了简洁只展示输入输出格式及数据范围。

核心思维

本题利用递推做的核心思想很简单，即当这个5x5数组的第一行被处理完过后，想要开启第一行仍然灭着的灯，则必须点击该灯的下一行的相同位置。

因此，只要确定好第一行如何选择，其他行也自然确定了，之需要判断该种情况是否满足题目条件即可。

如图所示：

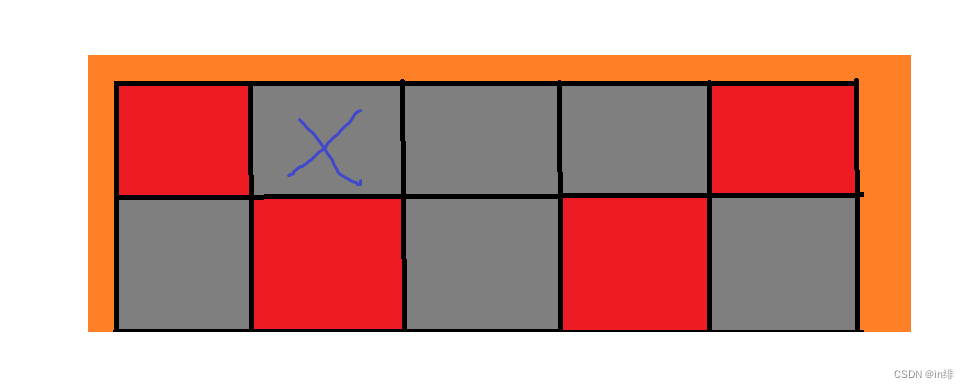
假设我们第一行只点一次，即被蓝色X的地方，点完后会变成这样：

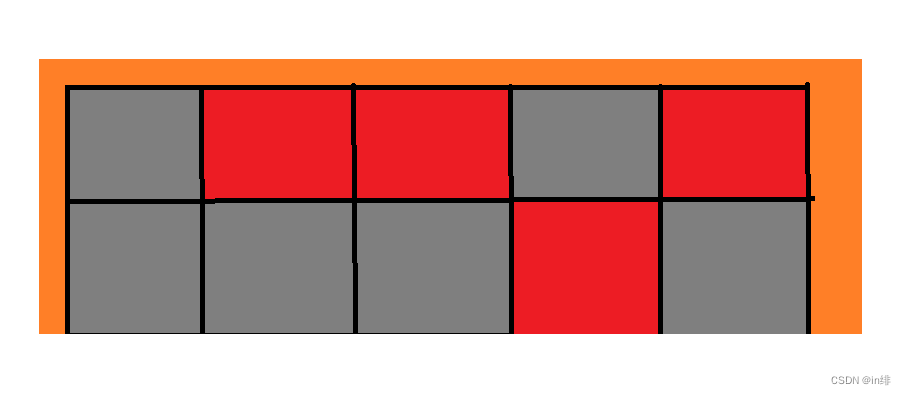
如果我们想让第一行的第一个、第四个变亮，那么第二行的第一个、第四个就是必点的。

因此，我们只需要枚举第一行的所有选法，然后就能递推出整个四方体的选法，最后判断成是否成立。

写出数据输入格式

首先，先在主函数里写出题目要求的输入格式。先输入一个n，随后进行n次循环，每次循环都读入25个数据放在一个二维数组arr里。为了传参的时候方便，我们把二维数组放在外面，像这样：

int arr[5][5];
int main()
{
	int n = 0;
	scanf("%d", &n);
	while (n--)
	{
		int i = 0;
		for (i = 0; i < 5; i++)
		{
			int j = 0;
			for (j = 0; j < 5; j++)
			{
				scanf("%1d", &arr[i][j]);
			}
		}
		//...
	}
	return 0;
}

注意： 本题在Acwing上数据输入时，每个数据之间没有空格，因此要控制scanf每次读取数据的宽度。代码中的“//...”代表接下来从此处开始写。

枚举第一行的选择

这里我们使用递归的方法，即在1 ~ 5里面选出1 ~ 5个数，每一种选法都是一种第一行的选择。创建递归函数dfs（int step），step代表当前枚举的位置，在外面创建数组choose代表递归时每个位置的状态，每次枚举当前位置选或者不选，五个位置都枚举结束后就代表形成了一种情况，随后利用判断函数jud对这种情况进行判断。

int main()
{
		//...
		dfs(0);//dfs的位置
	}
	return 0;
}

int arr[5][5];
int choose[5];
void dfs(int step)
{
	if (step == 5)
	{
		jud(choose);
		return;
	}
	//选
	choose[step] = 1;
	dfs(step + 1);
	choose[step] = 0;

	//不选
	dfs(step + 1);

}

判断情况是否成立（1）

随后我们进行判断函数jud的书写，为了防止同一组数组不同的情况互相影响，我们创建一个临时的数组 _arr，复制arr的信息到其中，随后对 _ arr进行操作。

之后创建i和j，分别用于遍历行和列。

由于i和j的值不同，点灯还是灭灯的个数也不同（因为有可能在边界）。因此，我们创建一个函数change，用于改变arr【i】【j】周围能改变的灯的亮灭情况。

void jud(int* choose)
{
	int _arr[5][5];
	memcpy(_arr, arr, 25 * 4);
	//对第一行进行操作

	int i = 0;//用于遍历行
	int j = 0;//用于遍历列

	for (j = 0; j < 5; j++)
	{
		if (choose[j] == 1)//相当于arr【0】【j】被选择了
		{
			change(_arr, 0, j);
			//...
		}
	}

}

实现亮灭改变函数

罗列情况，改变周围灯的亮灭情况，如果你不想写这么多的代码，也可以把刚开始创建的数组改为7x7大小，就可以不用考虑边界了。

void change(int _arr[5][5], int i, int j)
{
	_arr[i][j] = !_arr[i][j];
	if (i == 0)
	{
		_arr[i + 1][j] = !_arr[i + 1][j];
		if (j == 0)
		{
			_arr[i][j+1] = !_arr[i][j+1];
		}
		else if (j == 4)
		{
			_arr[i][j-1] = !_arr[i][j-1];
		}
		else
		{
			_arr[i][j - 1] = !_arr[i][j - 1];
			_arr[i][j + 1] = !_arr[i][j + 1];
		}
	}
	else if (i == 4)
	{
		_arr[i - 1][j] = !_arr[i - 1][j];
		if (j == 0)
		{
			_arr[i][j + 1] = !_arr[i][j + 1];
		}
		else if (j == 4)
		{
			_arr[i][j - 1] = !_arr[i][j - 1];
		}
		else
		{
			_arr[i][j - 1] = !_arr[i][j - 1];
			_arr[i][j + 1] = !_arr[i][j + 1];
		}
	}
	else
	{
		_arr[i - 1][j] = !_arr[i - 1][j];
		_arr[i + 1][j] = !_arr[i + 1][j];
		if (j == 0)
		{
			_arr[i][j+1] = !_arr[i][j+1];
		}
		else if (j == 4)
		{
			_arr[i][j - 1] = !_arr[i][j - 1];
		}
		else
		{
			_arr[i][j - 1] = !_arr[i][j - 1];
			_arr[i][j + 1] = !_arr[i][j + 1];
		}
	}
}

判断情况是否成立（2）

因为对第一行的每一次选择也算走了一步，所以在每种情况下设置一个变量time，记录当前走了几步，一旦time超过6，就立马return。

注意： 第一行只有五个数，因此在第一行的选择中time不可能超过6，因此不需要在对第一行的选择中进行判断。

void jud(int* choose)
{
	int _arr[5][5];
	memcpy(_arr, arr, 25 * 4);
	int time = 0;
	//对第一行进行操作

	int i = 0;//用于遍历行
	int j = 0;//用于遍历列

	for (j = 0; j < 5; j++)
	{
		if (choose[j] == 1)//相当于arr【0】【j】被选择了
		{
			time++;
			change(_arr, 0, j);
		}
	}
	//...
	//对2，3，4，5行进行操作
}

随后对第2，3，4，5行进行选择，对第二行的选择次数，是源于第一行选择完之后还有几个灭着的灯。

因此，我们对上一行进行遍历，如果_arr【i-1】【j】==0，就把time+1，同时点一下_arr【i】【j】。

注意： 此时，time已经有可能超过6了，因此需要进行判断。

void jud(int* choose)
{
	int _arr[5][5];
	memcpy(_arr, arr, 25 * 4);
	int time = 0;
	//对第一行进行操作

	int i = 0;//用于遍历行
	int j = 0;//用于遍历列

	for (j = 0; j < 5; j++)
	{
		if (choose[j] == 1)//相当于arr【0】【j】被选择了
		{
			time++;
			change(_arr, 0, j);
		}
	}
	//...
	//对2，3，4，5行进行操作
	for (i = 1; i < 5; i++)
	{
		for (j = 0; j < 5; j++)
		{
			if (_arr[i - 1][j] == 0)
			{
				time++;
				if (time > 6)
				{
					return;
				}
				change(_arr, i, j);
			}
		}
	}
	//...
}

现在，我们已经对1 ~ 5行全部选择完毕，但是不确定是否全部都为1，因此需要进行遍历一次，一旦出现为0的情况，说明这种情况不可取，马上返回。

	//检测数组中是否全部为1
	for (i = 0; i < 5; i++)
	{
		for (j = 0; j < 5; j++)
		{
			if (_arr[i][j] == 0)
			{
				return;
			}
		}
	}
	//...
	//运行到这里，说明此种方案可行

对输出数据的处理

题目要求我们输出所有可行的方案中步数最少的一种所消耗的步数，如果没有可行方案则返回-1。

因此，我们设置一个全局变量min_time并令其初始化为一个大于6的数，一旦出现一个time小于min_time，就把min_time更新为time。

如果还有更小的time，就能再次更新。

int arr[5][5];
int choose[5];
int min_time = 10;

	//运行到这里，说明此种方案可行
	min_time = time;
	return;
	//...

随后，我们进行最后的处理。

当dfs（0）结束之后，我们得到了一个min_time，因为它的初始值大于6，所以只要有可行方案存在，该值就一定会被改变，否则，它就依然还是原来的值。

所以，我们设置一个if语句，如果该值为10（初始值），代表没有可行方案，打印-1后换行。

如果该值不等于10，就打印这个数后换行，代表最小步数为该值。

注意： 因为min_time是我们在全局定义的，因此打印完了以后不要忘记再将其重新赋值为10哦。（博主改了很久才想到这一点，TAT）

int main()
{
	int n = 0;
	scanf("%d", &n);
	while (n--)
	{
		int i = 0;
		for (i = 0; i < 5; i++)
		{
			int j = 0;
			for (j = 0; j < 5; j++)
			{
				scanf("%1d", &arr[i][j]);
			}
		}
		dfs(0);
		if (min_time == 10)
		{
			printf("-1\n");
		}
		else
		{
			printf("%d\n", min_time);
			min_time = 10;
		}
	}

	return 0;
}

感谢您的阅读与耐心~ 如有错误烦请指出~