【数值计算方法】线性方程组迭代算法的Python实现

线性方程组迭代算法的Python实现

jacobi,GS,SOR迭代法

def JacobiIter(A:np.ndarray,
                b:np.ndarray,
                tol:float=1e-5,
                maxIter:int=100)->Tuple[np.ndarray,np.ndarray]:
    """使用Jacobi迭代法求解线性方程组Ax=b

    input:
    A: np.ndarray, 系数矩阵
    b: np.ndarray, 右端常数
    tol: float, 误差限
    maxIter: int, 最大迭代次数

    output:
    x: np.ndarray, 解向量
    errors: np.ndarray, 误差序列
    """
    from numpy import dot
    from numpy.linalg import norm
    x0=np.zeros(b.shape)
    L=-1*np.tril(A,k=-1).copy()
    U=-1*np.triu(A,k=1).copy()
    D=np.diag(np.diag(A)).copy()
    Dinv=np.linalg.inv(D)
    errors=[]
    for i in range(maxIter):
        x_next=dot(Dinv,(dot((L+U),x0)+b))
        # error check
        error=norm(b-dot(A,x_next),2)/norm(b,2)
        errors.append(error)
        if error<tol:
            return x_next,np.array(errors)
        else:
            x0=x_next

def GaussIter(A:np.ndarray,
                b:np.ndarray,
                tol:float=1e-5,
                maxIter:int=100)->Tuple[np.ndarray,np.ndarray]:
    """使用Gauss-Seidel迭代法求解线性方程组Ax=b

    input:
    A: np.ndarray, 系数矩阵
    b: np.ndarray, 右端常数
    tol: float, 误差限
    maxIter: int, 最大迭代次数

    output:
    x: np.ndarray, 解向量
    errors: np.ndarray, 误差序列
    """
    from numpy import dot
    from numpy.linalg import norm
    x0=np.zeros(b.shape)
    L=-1*np.tril(A,k=-1).copy()
    U=-1*np.triu(A,k=1).copy()
    D=np.diag(np.diag(A)).copy()
    DsubLinv=np.linalg.inv(D-L)
    errors=[]
    for i in range(maxIter):
        x_next=DsubLinv.dot(U).dot(x0)+DsubLinv.dot(b)
        # error check
        error=norm(b-dot(A,x_next),2)/norm(b,2)
        errors.append(error)
        if error<tol:
            return x_next,np.array(errors)
        else:
            x0=x_next

def SORIter(A:np.ndarray,
                b:np.ndarray,
                w:float=1.0,
                tol:float=1e-5,
                maxIter:int=100)->Tuple[np.ndarray,np.ndarray]:
    """使用SOR迭代法求解线性方程组Ax=b

    input:
    A: np.ndarray, 系数矩阵
    b: np.ndarray, 右端常数
    w: float, 松弛因子(0~2.0)
    tol: float, 误差限
    maxIter: int, 最大迭代次数

    output:
    x: np.ndarray, 解向量
    errors: np.ndarray, 误差序列
    """
    from numpy import dot
    from numpy.linalg import norm
    x0=np.zeros(b.shape)
    L=-1*np.tril(A,k=-1).copy()
    U=-1*np.triu(A,k=1).copy()
    D=np.diag(np.diag(A)).copy()

    DsubOmegaLinv=np.linalg.inv(D-w*L)
    errors=[]
    for i in range(maxIter):
        x_next=DsubOmegaLinv.dot((1-w)*D+w*U).dot(x0)+w*DsubOmegaLinv.dot(b)
        # error check
        error=norm(b-dot(A,x_next),2)/norm(b,2)
        errors.append(error)
        if error<tol:
            return x_next,np.array(errors)
        else:
            x0=x_next

• 验证

import numpy as np
from formu_lib import *
A=np.array([[2,-1,0],
            [-1,3,-1],
            [0,-1,2]])
b=np.array([1,8,-5])
extractVal=np.array([2,3,-1])

x1,er1=JacobiIter(A,b)
x2,er2=GaussIter(A,b)
x3,er3=SORIter(A,b,1.2)

ind1,ind2,ind3=list(range(len(er1))),list(range(len(er2))),list(range(len(er3)))
plotLines([ind1,ind2,ind3],[er1,er2,er3],["Jacobi iter error","Gauss iter error","SOR iter error"])

showError(x1,extractVal)
showError(x2,extractVal)
showError(x3,extractVal)

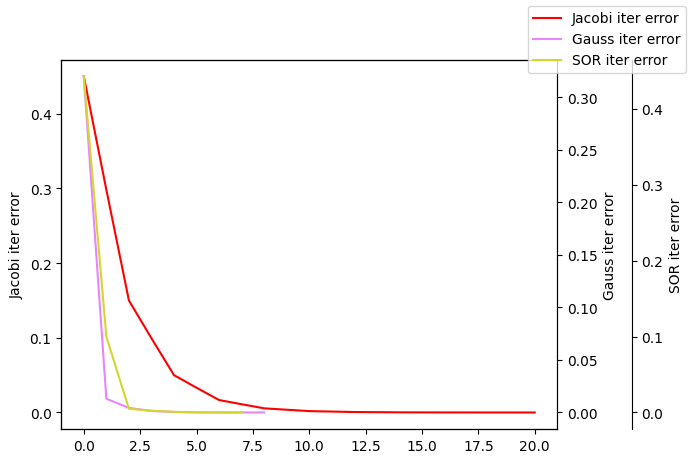
# 雅可比迭代法
数值解: [ 1.9999746   2.99999435 -1.0000254 ],
精确解: [ 2  3 -1],
误差: 9.719103983280175e-06
# GS迭代法
数值解: [ 1.9999619  2.9999746 -1.0000127],
精确解: [ 2  3 -1],
误差: 1.2701315856479742e-05
# SOR迭代法
数值解: [ 2.00001461  2.999993   -1.00000098],
精确解: [ 2  3 -1],
误差: 4.338862621105977e-06

正定对称线性方程组的不定常迭代:最速下降法,共轭梯度法

def SPDmethodSolve(A:np.ndarray,
                    b:np.ndarray,
                    tol:float=1e-5,
                    maxIter:int=200)->Tuple[np.ndarray,np.ndarray]:
    """使用最速下降法求解线性方程组Ax=b

    input:
    A: np.ndarray, 系数矩阵,必须是对称正定矩阵
    b: np.ndarray, 右端常数
    tol: float, 误差限
    maxIter: int, 最大迭代次数

    output:
    x: np.ndarray, 解向量
    errors: np.ndarray, 误差序列
    """
    from numpy import dot
    from numpy.linalg import norm
    x0=np.zeros(b.shape)
    i,errors=0,[]
    while True :
        if i>maxIter:
            maxIter=1.5*maxIter
            print(f"迭代次数过多,自动调整为 {maxIter}")
        # 计算残量r^k作为前进方向.
        r=b-dot(A,x0)
        # 计算前进距离a_k
        a=InnerProduct(r,r)/InnerProduct(dot(A,r),r)
        x_next=x0+a*r
        error=norm(b-dot(A,x_next),2)/norm(b,2)
        errors.append(error)
        if errors[-1]<tol:
            return x_next,np.array(errors)
        else:
            x0=x_next
            i+=1

def conjGrad(A:np.ndarray,
                b:np.ndarray,
                tol:float=1e-5,
                maxIter:int=200)->Tuple[np.ndarray,np.ndarray]:
    """使用共轭梯度法求解线性方程组Ax=b

    input:
    A: np.ndarray, 系数矩阵,必须是对称正定矩阵
    b: np.ndarray, 右端常数
    tol: float, 误差限
    maxIter: int, 最大迭代次数

    output:
    x: np.ndarray, 解向量
    errors: np.ndarray, 误差序列
    """
    from numpy import dot
    from numpy.linalg import norm
    # 选择初值x0,初始方向p0=r0=b-Ax0
    x0=np.zeros(b.shape)
    i,errors=0,[]
    r0=b-dot(A,x0)
    p_0=b-dot(A,x0)
    errors.append(norm(r0,2)/norm(b,2))
    while True :
        if i>maxIter:
            maxIter=1.5*maxIter
            print(f"迭代次数过多,自动调整为 {maxIter}")
        # 计算a_k,x^{k+1}=x_k+a_k*p_k
        a_k=InnerProduct(r0,p_0)/InnerProduct(dot(A,p_0),p_0)
        x_next=x0+a_k*p_0
        # 计算下一步的残量
        r_k_next=b-dot(A,x_next)
        errors.append(norm(r_k_next,ord=2)/norm(b,2))
        # 如果残量足够小,则停止迭代
        if errors[-1]<tol:
            return x_next,np.array(errors)
        else:
            # 计算下一步的搜索方向
            beta_k=-1*InnerProduct(r_k_next,A.dot(p_0))/InnerProduct(p_0,A.dot(p_0))
            p_0=r_k_next+beta_k*p_0
            x0=x_next
            i+=1

• 验证

from formu_lib import *
import numpy as np

A=np.array([[4,-1,0],
            [-1,4,-1],
            [0,-1,4]])
b=np.array([3,2,3])
extractVal=np.array([1,1,1])

x1,er1=SPDmethodSolve(A,b,1e-6)
x2,er2=conjGrad(A,b,1e-6)

plotLines([list(range(len(er1))),list(range(len(er2)))],[er1,er2],["SPD method error","conjugate gradient error"])

showError(x1,extractVal)
showError(x2,extractVal)

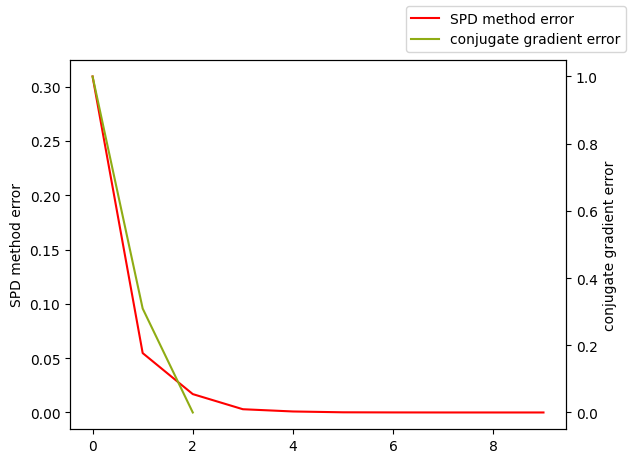
# SPD method
数值解: [0.99999951 0.99999951 0.99999951],
精确解: [1 1 1],
误差: 4.891480784863234e-07
# conjugate gradient method
数值解: [1. 1. 1.],
精确解: [1 1 1],
误差: 0.0