3.4模拟赛T4 题解

步骤一：枚举

注意到本题的 \(n,m\le 50\) 使得我们不能直接对 o 进行状压。因为 o 可能有很多个。

而题目又给了数据的另一个特点就是* 不超过 \(12\) 个。

所以可能会存在 \(O(2^{*的个数})\) 这样的一个时间复杂度。

所以考虑将所有的 o 取为中心，而 * 我们用二进制来枚举每一个*是否取为中心。

那么问题就转化为对于格子中，已经规定了一些点取为中心，求在此情况下摆放积木的方案数。

步骤二：判断无解、根据限制条件建图

我们发现，对于一个中心，如果可以，我们有 \(4\) 种放置方式。而当我们放置一个积木后，可能会导致周围的中心格子积木的放置方式变少。因为不能重叠。

我们称 使一个中心的放置方式确定且唯一 为 定向。

我们现在要放黑色圆圈这个位置，那么可能导致放置方式受影响的格子为下图：

那么受影响的格子分为三类：红格子（相邻），黄格子（有一个角公共），蓝格子（中间隔了一个位置）。

情况一： 红格子（相邻）

注意此时因为这两个格子（一红一黑）相邻，所以这两个格子的放置方式是定的，也就是被定向了。

也就是当黑格子周围有且仅有一个红格子或 超出边界的格子时，黑格子被定向了。

但是如果黑格子周围有 \(>1\) 个红格子或 超出边界的格子，会导致黑格子无论如何都放不了。此情况是无解的。

粗略来讲，这个红格子只是指代一定填不了的格子。

情况二：蓝格子（中间隔了一个格子）

此时中间隔的格子一定是空的。（不然会被上一步返回无解）

如果其中有且仅有一个被定向了，那么另一个也会被跟着定向。可以理解为 定向的传导。因为中间的格子是空的，所以被定向的格子一定是因为黄色格子被占而导致该格子放置时一定占了二者中间的位置。从而导致另一个格子也被定向。

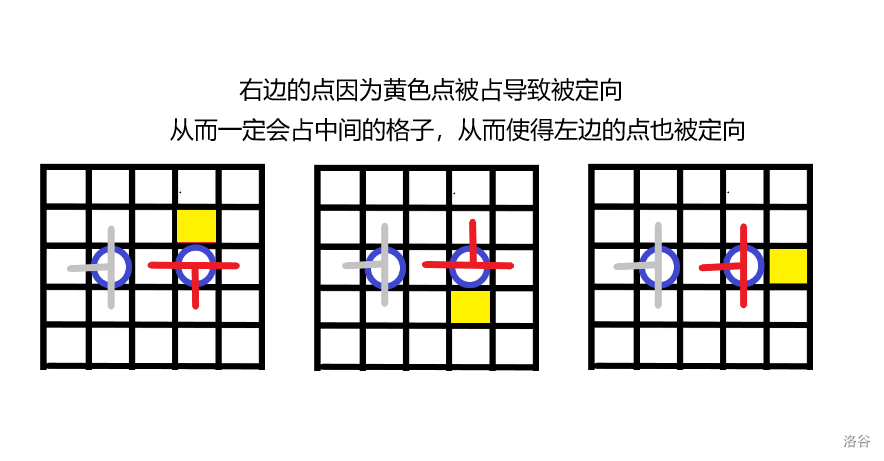
此后任意时候，如果其中的任意一个被定向了，那么另一个也会被定向。所以考虑将两个点之间连一条边，那么当一个点被定向后，它所在的连通块都会被定向。所以考虑用并查集维护这个边。

但是如果此前二者都被定向了，那么都会占中间的格子。所以无解。

特殊情况：构成环

我们在按上述情况进行建边时可能会遇到环，如下图：

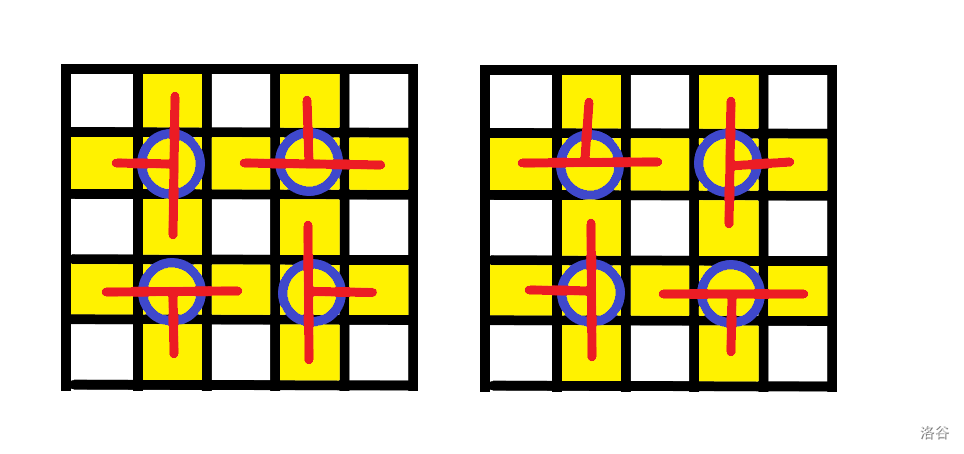
在连通块内没有任意一点被定向时，一共有两种情况。但是这两种情况所占的格子是一样的。是不是可以认为为某种意义上的“被定向了”呢？

此时我们可以模拟建边的过程。加入最后一条边时，两个点属于同一个连通块，如果两个点都被定向了，则无解，因为会重叠。否则就可以视作为某种意义上的“被定向了”，不过方案数需要 \(\times 2\)。

为了区分，我们在并查集中维护值 \(t=1\) 表示被非严格定向了（也就是包含这种情况），以及 \(t2=1\) 表示严格定向（不包含这种情况）。

那么对于合并点 \(x,y\)

• 如果 \(fa_x=fa_y\)

  当 \(t_{fa_x}=1\) 时无解。否则让 \(t_{fa_x}=1\)，不更新 \(t2_{fa_x}\)，因为 \(t2\) 不管这种情况。

• 如果 \(fa_x\neq fa_y\)

  让 \(x\gets fa_x，y\gets fa_y\)。

  当 \(t_{x}=t_{y}=1\) 时无解。否则让 \(fa_x=y\)，\(t_y|=t_x\)，\(t2_y|=t2_x\)。

情况三：黄格子（有一个角公共）

此时如果没有被定向，则一共存在两种情况。

而他们占的格子也一样。

其实这个东西与上面那个特殊情况很一样啊。因为有两种情况，且占的格子都一样。

而且还有更一样的，就是在一个连通块内，最多只会出现一个这个相邻的，或者那个成环的，否则无解。

因为这两个东西相当于定向了，当一个连通块被不同方向同时定了向时是无解的。

所以这个东西可以类似上面的维护。

直接进行连边。而且因为这种情况需要更改 \(t\) ，不更改 \(t2\)。所以需要再进行一次连边。

另一种理解方式

可以用 < 和 > 理解。

对于一次传导，相当于存在 >>>>或<<<< 的箭头。而上面的特殊情况和相邻情况相当于 <>。所以最终会形成一个类似 <<<<<<<>>>>>>。这也可以说明一个连通块最多只存在一个 <>。

步骤三：计算方案数

总方案为每个连通块的方案数的乘积。

分类讨论：

• 被严格定向，即 \(t2=1\)

  此时方案数为 \(1\)。

• 没有被定向（包括非严格），即 \(t=0，t2=0\)

  为了方便计算，我们还需在并查集过程中记录变量 \(sz\)，表示连通块大小。

  则无论怎么填我们都会空一个位置。（自己画图理解）

  而且我们发现，我们想让哪个位置空都行（除了中心）。

  所以方案数为中心的四联通格子。

  每个中心有 \(4\) 个四联通格子。但是会有重复。因为不存在环，所以此时并查集结构为一棵树。重复格子有 \(sz-1\) 个。

  所以方案数为 \(4\times sz-(sz-1)=3\times sz+1\)。

• 被非严格定向，没有被严格定向，即 \(t=1，t2=0\)

  此时方案数为 \(2\)。

最后最终答案就是枚举过程中各个答案之和。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#define LL long long
inline int read(){
	char c=getchar();bool f=0;int x=0;
	while(c > '9' || c < '0') f|=c=='-',c=getchar();
	while(c >= '0'&&c <= '9') x=(x<<1)+(x<<3)+(c^48),c=getchar();
	if(f) x=-x;return x;
}
const int N = 60,MOD = 1e9 + 7;

const int dx[5] = {0,0,-1,1},dy[5] = {-1,1,0,0};
int n,m,t[N * N],t2[N * N],fa[N * N],id[N][N],sz[N * N];
LL ans;
int mp[N][N],pow_2[N];
bool flag;

std::vector<std::pair<int,int> > k;
bool check(int x,int y)
{
	if(x < 1 || y < 1 || x > n || y > m) return true;
	return false;
}

int find(int x)
{
	return x == fa[x] ? x : fa[x] = find(fa[x]);
}

void merge(int x,int y)
{
	y = find(y);
	x = find(x);
	if(x == y)
	{
		if(t[x]) return flag = true, void();
		t[x] = 1;
	}else
	{
		if(t[x] && t[y]) return flag = true, void();
		t[y] |= t[x];
		t2[y] |= t2[x];
		fa[x] = y;
		sz[y] += sz[x];
	}
}

void solve()
{
	int idx = 0;
	flag = false;
	for(int i = 1;i <= n;++i)
	{
		for(int j = 1;j <= m;++j)
		{
			if(mp[i][j])
			{
				sz[++idx] = 1;
				fa[idx] = idx;
				id[i][j] = idx;
				t[idx] = t2[idx] = 0;
			}else id[i][j] = 0;
		}
	}

	for(int i = 1;i <= n;++i)
	{
		for(int j = 1;j <= m;++j)
		{
			if(!mp[i][j]) continue;

			int cnt = 0;
			for(int dir = 0;dir < 4;++dir)
			{
				int tx = i + dx[dir];
				int ty = j + dy[dir];
				cnt += int(check(tx,ty) || mp[tx][ty]);
			}
			if(cnt > 1)	return ;
			if(cnt == 1) t[id[i][j]] = t2[id[i][j]] = 1; 

			//在接下来的合并当中，我们不会把四个方向都考虑，因为一定可以到另一个点的时候，再考虑这个点的另外两个方向，省时间复杂度。
			if(!check(i - 2,j) && mp[i - 2][j]) merge(id[i - 2][j],id[i][j]);
			if(!check(i,j - 2) && mp[i][j - 2]) merge(id[i][j - 2],id[i][j]);
			if(!check(i - 1,j + 1) && mp[i - 1][j + 1])
			{
				merge(id[i - 1][j + 1],id[i][j]);
				merge(id[i - 1][j + 1],id[i][j]);//合并两次，第二次实际上是为了判断是否有解
			}
			if(!check(i - 1,j - 1) && mp[i - 1][j - 1])
			{
				merge(id[i - 1][j - 1],id[i][j]);
				merge(id[i - 1][j - 1],id[i][j]);
			}
			if(flag) return ;
		}
	}

	LL res = 1;
	for(int i = 1;i <= idx;++i)
	{
		if(find(i) == i && !t2[i])
		{
			if(!t[i]) res = res * 1ll * (3 * sz[i] + 1) % MOD;
			else res = res * 2 % MOD;
		}
	}
	ans += res;
	if(ans >= MOD) ans -= MOD;
}

int main()
{
	pow_2[0] = 1;
	for(int i = 1;i <= 15;++i) pow_2[i] = pow_2[i - 1] << 1;
	n = read();
	m = read();
	for(int i = 1;i <= n;++i)
	{
		char ch[N];
		scanf("%s",ch + 1);
		for(int j = 1;j <= m;++j)
		{
			if(ch[j] == '*') k.push_back({i,j});
			else if(ch[j] == 'o') mp[i][j] = 1;
		}
	}

	int num = k.size();
	for(int i = 0;i < pow_2[num];++i)
	{
		for(int j = 0;j < num;++j) if(i & pow_2[j]) mp[k[j].first][k[j].second] = 1;
		solve();
		for(int j = 0;j < num;++j) if(i & pow_2[j]) mp[k[j].first][k[j].second] = 0;
	}

	printf("%lld",ans);
	return 0;
}