SciTech-Mathmatics-Probability+Statistics:Quantifing Uncertainty_统计数据分析:朱怀球PKU-3-Sampling Theory 统计抽样理论基础

Statistics & Data Analysis

— Zhu Huaiqiu, Peking University

《统计与数据分析》, 朱怀球, 北京大学

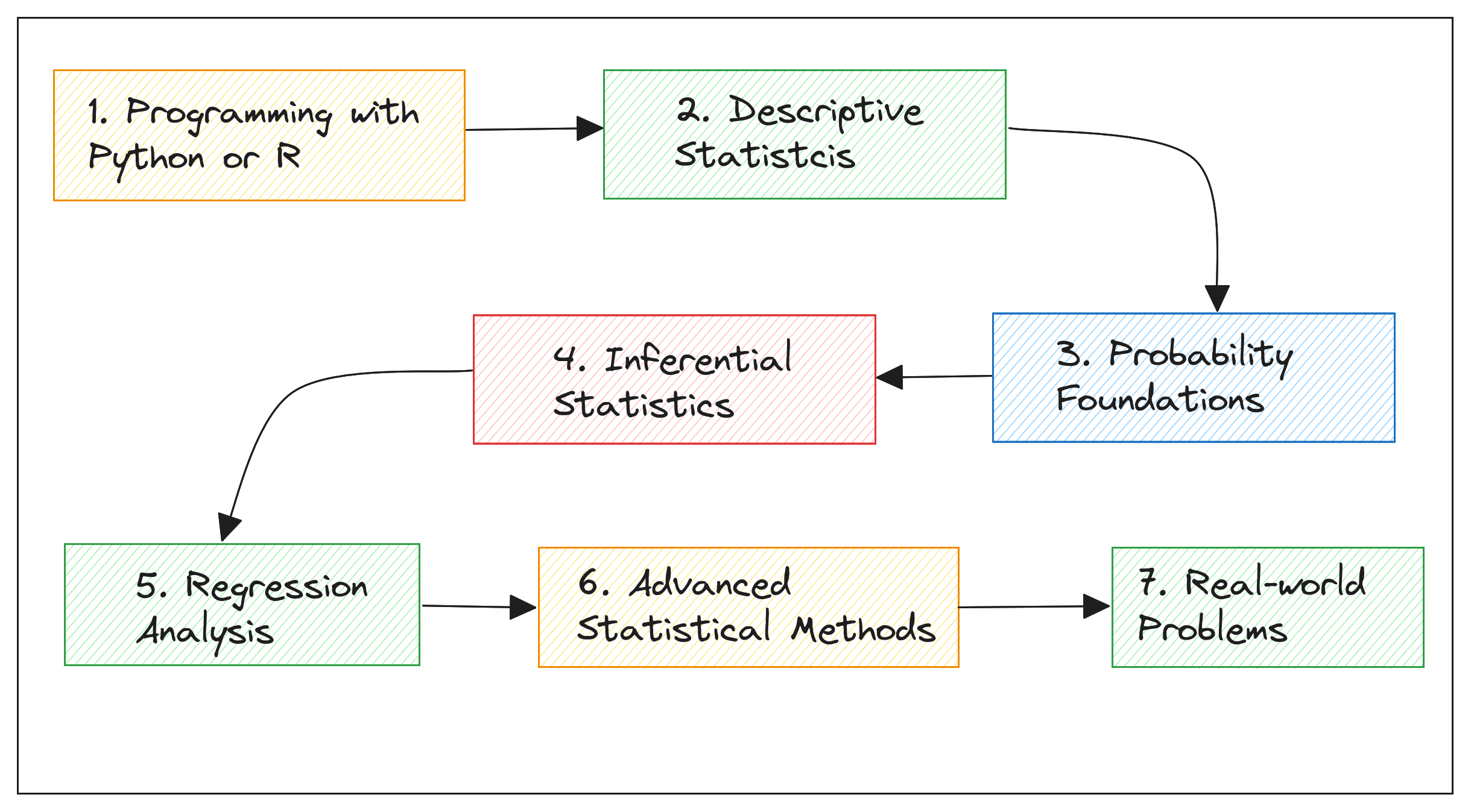
7 Steps

§3 统计抽样理论基础

"\(\large \text{ Get your facts first, then you can distort them as you please.}\)"

— \(\large Mark\ Twin\)

"\(\large \text{ Our behavior, attitudes, and sometimes actions are based on samples.}\)"

— \(\large Elements\ of\ Sampling\ Theory\ and\ Methods\)

3.1 统计抽样的基本概念

\[\large \begin{array}{l}\\
\bm{ Statistical\ Inference }\ Theory \begin{cases} \bm{ Hypothesis\ Testing }\ Theory \\
\bm{ Parameter\ Estimation } \ Theory \\ \bm{ Statistical\ Sampling }\ Theory \\ \bm{ Probability\ }\ Theory \\
\end{cases} \\
\end{array} \]

Comparing: Statistics 和 Probability

Statistics基本思想( 总体 — 样本 — 总体 )

\(\large \begin{array}{rl} \\
X :& \bm{ Population },\ Statistics: \mu,\ \tau, \sigma, \ \sigma^2 \\
\Theta :& \bm{ Parameter\ Space } \\
\theta :& \bm{ Parameter } \\
\{X_i\}:& \bm{Sample} ,\ Statistics: \overset{-}{x}, \ \\
\overset{\sim}{\Theta}:& \bm{ Parameter\ Estimation } \\
\end{array}\)

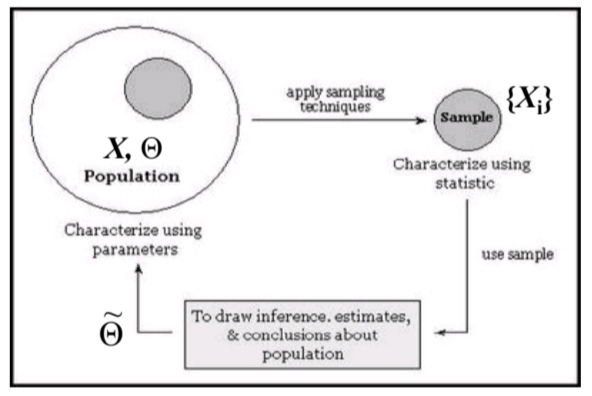
Sampling Concept(抽样 的 概念)

For \(\large \text{ one existing }\) \(\large \bm{Measuring\ Population }\) (named \(\large \bm{\text{Simple Population}}\)),

sample \(\large \bm{Measuring\ Sample}\) (named \(\large \bm{\text{Simple Sample}}\) ) from the \(\large \bm{\text{Simple Population}}\)), using specific sort of \(\large \bm{\text{Inference Method}}\).

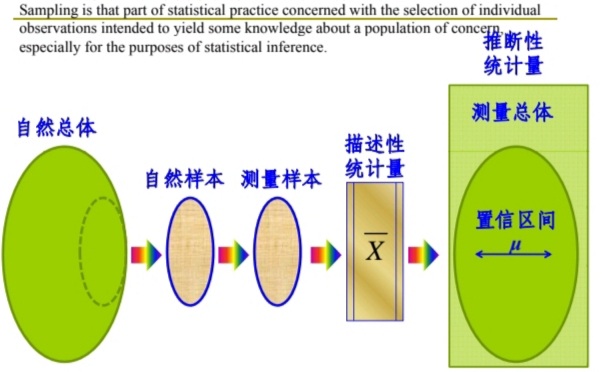
\(\large \begin{array} {lll} \\
\bm{ Population(Natural) } &\Rightarrow \bm{ Sample(Natural) } &\Rightarrow \bm{ Sample(Measuring) } \\
\bm{ Sample(Measuring) } &\Rightarrow \bm{ Descriptive\ Statistics } &\Rightarrow \bm{ Population(Measuring) } \end{array}\)

Sampling & Statistics

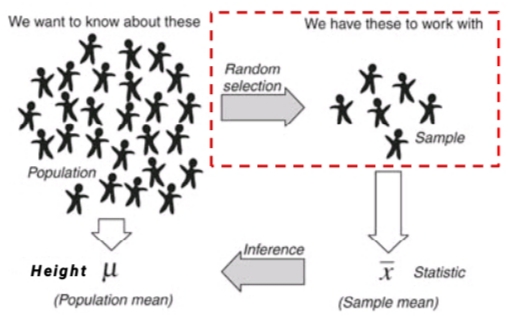
Parameters & Statistics

• Parameters(of Population) and Statistics(of Sample)

\[\large \begin{array}{lll}\\
\bm{ Statistical\ Theory } & \begin{cases} \bm{ Center\ Tendency } & \rightarrow \bm {Mean} \\
\bm{ Variation\ Tendency } & \rightarrow \bm {Variance, \ STD} \\
\end{cases} \\
\bm{ Probability\ Theory } & \begin{cases} \bm{ Center\ Tendency } & \rightarrow \bm {Expectation} \\
\bm{ Variation\ Tendency } & \rightarrow \bm {Variance} \\
\end{cases} \\
\end{array} \]

• 1.4.1 Statistics(统计变量) 和 Observation(观测) of Statistical Resources(统计资料)

  • Statistics(统计变量):

    研究对象的、可测量的特征
    
    且对于一组对象中的不同对象可以取不同的值。

  • Observation Value(观测值): 变量的每一个测量值(x,x)

    • Quanlitative Variable(定性变量): Non-Rankable观测值, 特征的 量值不能排序
    • Quantitative Variable(定量变量): Rankable 观测值, 特征的 数量可以排序
    • Discrete Variable
    • Continuous Variable

  • Statistical Function:

    • 函数关系，运用统计方法确定的，自变量和因变量之间的，
    • 只需要定义域、值域和两个变量间的对应关系,
      
      并不总是需要等式表达式

  • Statistical Resources(统计资料):

    观测结果组成的集合

    • 定性统计资料、定量统计资料
    • 连续统计资料、离散统计资料
    • 有效数字: 在观测尺度(或科学计算)中实际能够得到的所有数字
      
      常见问题:
      • \(\large 102个细胞\)
      • \(\large 10,100个细菌(精确到100) \ \rightarrow\ 10,050 \text{ ~ } 10,150\)
      • \(\large 23.4\%(23.437201\%?)\)
      • \(\large 4.15 \text{ ~ } 4.25\ \times\ 10^{-3}\)

• Observation of Statistics(统计变量的观测)

  统计资料测量值, 受各种随机因秦的影响

  • System Error(系统误差)

    System Error(系统误差)的大小,

    • 稳定(观测过程不变),
    • 可预测(用计算或实验方法可求得),
    • 可补偿(可修正或调整使其减少).

  • Random Error(随机误差):

    在相同条件下, 对同一Statistic的多次观测,
    
    由于各种 Random Factors, 会出现测量值时而偏大、时而偏小的误差现象, 这种类型的误差叫Random Error。
    
    在确定的测量条件, 对同一Statistic多次测量并用它的算术平均值, 作为它的测量结果, 能够比较好地减少Random Error。

    Statistical Rules of Random Error

    • 1. 绝对值相等的 正的与负的 误差 出现的机会相同
    • 1. Variance: 绝对值小的误差 比 绝对值大的误差 出现的机会多
    • 1. Range: 误差 不会超出 一定的范围。

• Descriptive Statistics(of Samples)

\[\large \begin{array}{lll}\\
\text {Samples Data} \begin{cases} \\
\bm{ Center\ Tendency } \overset{ \bm {Mean} }{ \rightarrow } & \begin{cases}
& \bm{ Mean } \\ & \bm{ Median } \\ & \bm{ Mode } \\
\end{cases} \\
\bm{ Variation\ Tendency } & \begin{cases}
& \overset{ \bm{Range} }{ \rightarrow } & \begin{cases}
\bm{ Max } \\ \bm{ Min } \\
\end{cases} \\
& \overset{ \bm{Quartiles} }{ \rightarrow } & \begin{cases}
\bm{ Up Quartile } \\ \bm{ Down Quartile } \\
\end{cases} \\
\end{cases} \\
\end{cases} \\
\end{array} \]

Population Parameters

设总体 \(\large X\) 容量为 \(\large N\), 个体取值为\(\large \{x _i \},\ i \in [1, N]\), 定义：

\(\large \begin{array}{ll} \\
\text{ population }mean : & \mu = \dfrac{1}{N} \overset{N}{\underset{i =1}{\sum}}{ x_i } \\
\text{ population }total : & \tau = \dfrac{1}{N} \overset{N}{\underset{i =1}{\sum}}{ x_i } = N \cdot \mu \\
\text{ population }variance : & \sigma^2 = \dfrac{1}{N} \overset{N}{\underset{i =1}{\sum}}{ (x_i - \mu)^2 } \\
\text{ population }standard\ deviation : & s = \sqrt{ \sigma^2 } \\
\end{array}\)

3.1.1 Statistical Model and Statistical Sampling Model

• Statistical Model:
  • 设 \(\large \{\Omega, F_{\Omega}\} \ 为可定义\ p.\ f.\ 的\ Measurable\ Space\),
    • \(\large \Omega\ is \text{ Sample Space }\)
    • \(\large F_{\Omega}\ is \text{ p. f.(Probability Function) }\)
      
      $\large \text{ for measuring the } \bm{Likelyhood} \text{ of the each } \bm{Outcome} $
  • \(\large \Phi \text{ 为其上的一个} \bm{ Distribution\ Cluster(概率分布族) }\),

\(\large 则三元组\{\Omega, F_{\Omega}, \Phi \}为\bm{ Statistical\ Model },\ 按是否取决于参数变量分两类\)

• \(\large \bm{ 参数统计模型 }:若 \bm{ 概率分布族 \Phi } \text{ 取决于某一} \ \bm{ \theta(Parameter\ Variable) }\)
  
  $\large \Phi =\{ P(\theta) | \theta \in \Theta,\ where\ \Theta \text{ is the }\ \bm{ Parameter\ Space }\} $
• \(\large \bm{ 非参数统计模型 }:\ \bm{ 概率分布族 \Phi } \text{ 不取决于任何} \ \bm{Parameter\ Variable}\)

• 乘积模型 和 重复抽样模型
  
  \(\large 设\ \{\Omega, F_{\Omega}, \Phi \}\ 和 \ \{\Omega', F_{\Omega}', \Phi' \}\ 为两个\ Statistical\ Model\),
  
  $\large 则\bm{ 乘积模型 } \{ \Omega \bigotimes \Omega', F_{\Omega} \bigotimes F_{\Omega}', \Phi \bigotimes \Phi' \} 记作 \{ \Omega, F_{\Omega}, \Phi \} \bigotimes \{\Omega', F_{\Omega}', \Phi' \} \ $
  • $\large n\ 个\bm{等同}的\ \{\Omega, F_{\Omega}, \Phi \}\ 的\bm{乘积模型}称 \bm{ 重复抽样模型 },记为\{ \Omega, F_{\Omega}, \Phi \}^n $
  • \(\large \bm{乘积模型} \text{ 实际等于 }\bm{独立观察系统}\)
  • $\large \bm{重复抽样模型} \text{ 等于 }\bm{对一个观测对象} \text{ 进行 }\bm{有限次独立抽样结果} \text{ 的 }\bm{描述} $。

3.1.2 Sampling Design

\(\large \text{ Results from } \bm{probability\ theory} \text{ and } \bm{statistical\ theory} \text{ are } ,\)

\(\large employed\ to\ \bm{guide\ practice\ of\ sampling}.\)

\(\large Random\ Sampling\)(随机抽样, 简称抽样)：

\(\large \text{ for } \bm{observing\ the\ elements\ of\ Population\ X },\)

\(\large 由其 \text{ 按照 } \bm{一定的概率} 抽取 \bm{\ Some\ Individuals}\).

\(\large Random\ Sample\)(随机样本, 简称样本)：

\(\large 按照\bm{一定的概率}由Population \ \bm{X} =\{ x_i \},\ i \in [1, N] 抽取\bm{作为总体代表}\ 的\)

\(\large \bm{\ Some\ Individuals\ 的集合} \ \\{ X_1, X_2, \dots , X_n \\},\ n<N,\)

\(\large\ 称为\ \bm{ 容量为\ n\ 的Sample\ X} \ \\{ X_i \\}, \ i \in [1, n]\)

讨论

1. 构成某一样本的每一个体都必须取自某一特定的统计总体,
   
   不允许该总体之外的个体计入该总体的样本;
2. 样本个体的抽取应是按一定的概率进行的，而具体样本的产生应是随机的,
   
   因此必须排除 人的主观因素 对 样本个体、抽取 和 样本生成 的干扰；
3. Sample是Population的代表，带有其 Distribution 信息;
   • 因而, 能够 推断Population的Distribution规律；
   • 然而，Sample只是Population的一个subset, 有随机性;
     
     因此，由Sample推断Population, 会产生 代表性误差。

\(\large Random\ Sampling\)的优点

\(\large Random\ Sampling\)是按照 Probability 来进行的，

即 Population 的任一 Individual 都按照 某一特定的Probability 有可能被选择，

产生的 Sample 的组成 因此是 随机的。

1. 客观: 可避免抽样者有意或无意的偏好；
2. 经济: 以尽可能小容量的Sample 来实现对Population 尽可能客观的Statistical Inference；
3. 容差: 可较好地估计出由Sampling Method带来的Error；
4. 可控: 可根据对Sampling Error的要求来设计Sample Size。
5. 工业化革命的直接产物: 大规模制造要求标准化设计和制造,
   
   对制造过程的质量控制, 直接诞生了统计抽样思想和技术.

根据 Statistics of Samples 对 Parameters of Population 进行 Estimation估计

\(\large \begin{array}{ll} \\
\text{ based on Statics of Samples estimate Parameters of Population } \\
\text{ hypothesis, } Population\ Size = N, \\
\text{ a }Simple\ Random\ Sample \text{ is } (X_1,\ X_2,\ \cdots,\ X_n), \\
Statistics\ of\ Samples \text{ as } estimate\ value \text{ of } Parameters\ of\ Population. \\
\\
\text{ Some }\ usually\ used\ estimations \text{ are }: \\
\end{array}\)

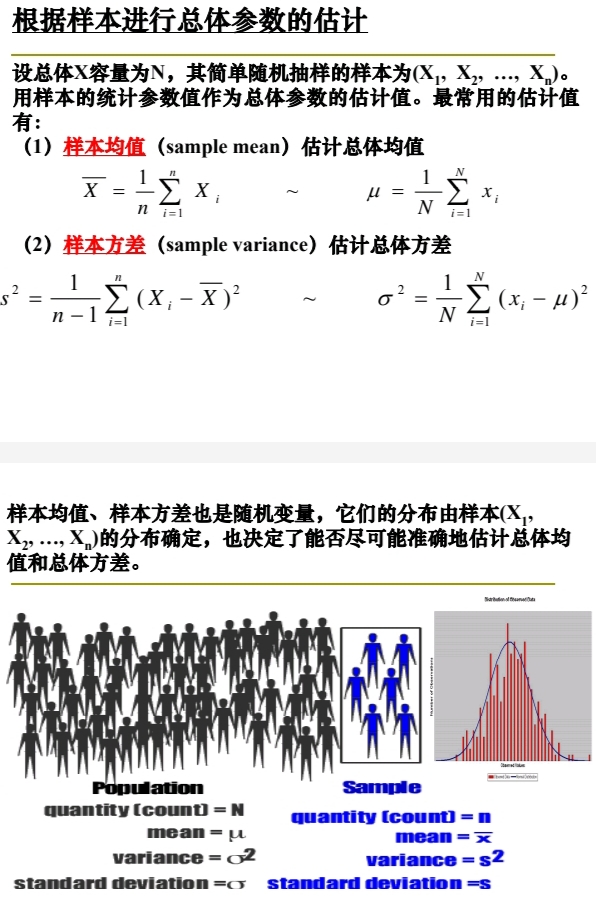
\(\large (1)\ Sample\ mean \text{ estimate } Population\ mean\)

\(\large \begin{array}{ll} \bm{ \overset{-}{X} } = \dfrac{1}{n} \overset{n}{\underset{i=1}{\sum}} {X_i} & \sim & \bm{ \mu } = \dfrac{1}{N} \overset{N}{\underset{i=1}{\sum}} {x_i} \end{array}\)



\(\large (2)\ Sample\ variance \text{ estimate } Population\ variance\)

\(\large \begin{array}{ll} \bm{ s^2 } = \dfrac{1}{n-1} \overset{n}{\underset{i=1}{\sum}} { ( X_i - \overset{-}{X} )^2 } & \sim & \bm{ \sigma^2 } = \dfrac{1}{N} \overset{N}{\underset{i=1}{\sum}} { (x_i - \mu)^2 } \end{array}\)

\(\large Sample\ mean\) and \(\large Sample\ variance\) are also \(\large Random\ Variables\),

their $\large Distribution $ are determined by the $\large Distribution $ of \(\large Sample\ (X_1,\ X_2,\ \cdots,\ X_n)\) that also determines if we can estimate the \(\large Population\ mean\) and \(\large Population\ variance\) as accurate as possible。

\(\large \begin{array}{rrll} \\
\bm{ Population } & \bm{ Parameters } & \bm{ Statistics } & \bm{ Sample } \\
quantity(count)\ =& \bm{ N } & \bm{ n } &=\ quantity (count) \\
mean\ =& \bm{ \mu } & \bm{ \overset{-}{x} } &=\ mean \\
variance \ =& \bm{ \sigma^2 } & \bm{ s^2 } &=\ variance \\
standard\ deviation \ =& \bm{ \sigma } & \bm{ s } &=\ standard\ deviation \\
\end{array}\)

Example:

• \(\large X_{\theta_1} \sim {\mathcal {N}}(\mu_1 ,\sigma_1 ^{2})\)
• \(\large X_{\theta_2} \sim {\mathcal {N}}(\mu_2 ,\sigma_2 ^{2})\)
• parameter vector is \(\large \theta = [\mu, \sigma^{2}]\)