topcoder srm 535 div1

problem1 link

对于每个质因子$p$，枚举其出现的最少次数以及最多次数分别在哪个数字中．

problem2 link

分数规划．题目是求$\frac{3600K+\sum_{i=0}^{K-1}a_{c_{i}}p_{c_{i}}}{\sum_{i=0}^{K-1}a_{c_{i}}}*totalWork$.其中$c_{i}$是选出的第$i$个元素．二分$\frac{3600K+\sum_{i=0}^{K-1}a_{c_{i}}p_{c_{i}}}{\sum_{i=0}^{K-1}a_{c_{i}}}$的值，然后选择$a_{i}(result-p_{i})$中最大的$K$个，看是否大于$3600K$.

problem3 link

到达最下面一行或者最右边一列时，只能朝一个方向走．设$f(i)$表示从(0,0)走到(n-1,i)的方案数（最后一步是从(n-2,i)到(n-1,i)），以及$g(i)$表示从$(0,0)$走到(i,m-1)的方案数（最后一步从$(i,m-2)$到(i,m-1)）．这两个是类似的．考虑$f(i)$.

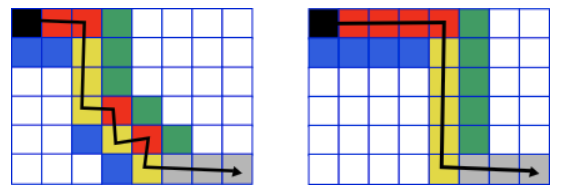
如下面的图示($n=6,m=8,i=4$)的两种走法，可以发现，横向走了红色的四个以及纵向走了黄色的５个，且最后一步到达$(n-1,i)$是黄色．

每次横向走时，需要对应的红色大于等于对应的蓝色;纵向走时，需要对应的黄色大于对应的绿色．

从(0,0)走到$(n-1,i)$一共走了$(i+n-1)$个格子，其中红色可以选择在这个序列的前$(i+n-2)$个中出现（最后一个一定是黄色）．

code for problem1

#include <vector>
using namespace std;

class FoxAndGCDLCM {
  using Type = std::pair<long long, int>;
public:
  long long get(long long G, long long L) {
    if (G > L) {
      return -1;
    }
    std::vector<Type> a = split(G);
    std::vector<Type> b = split(L);
    merge(a, b);
    for (size_t i = 0; i < a.size(); ++i) {
      if (a[i] > b[i]) {
        return -1;
      }
    }
    min_value = -1;
    dfs(0, a, b, 1ll, 1ll);
    return min_value;
  }
private:

  void dfs(int dep, const std::vector<Type> &a, std::vector<Type> &b,
      long long x, long long y) {
    if(dep == a.size()) {
      if (min_value == -1 || min_value > x + y) {
        min_value = x + y;
      }
      return;
    }
    const long long p = pow(a[dep].first, a[dep].second);
    const long long q = pow(b[dep].first, b[dep].second);
    dfs(dep + 1, a, b, x * p, y * q);
    dfs(dep + 1, a, b, x * q, y * p);
  }

  std::vector<Type> split(long long x) {
    std::vector<Type> result;
    for (long long t = 2; t * t <= x; ++t) {
      if (x % t == 0) {
        int num = 0;
        while (x % t == 0) {
          x /= t;
          ++num;
        }
        result.emplace_back(t, num);
      }
    }
    if (x > 1) {
      result.emplace_back(x, 1);
    }
    return result;
  }
  void merge(std::vector<Type> &a, std::vector<Type> &b) {
    std::vector<Type> ra, rb;

    std::size_t i = 0, j = 0;
    while (i < a.size() || j < b.size()) {
      if (i == a.size() || (j < b.size() && a[i].first > b[j].first)) {
        rb.emplace_back(b[j]);
        ra.emplace_back(b[j].first, 0);
        ++j;
      } else if (j == b.size() || (i < a.size() && a[i].first < b[j].first)) {
        ra.emplace_back(a[i]);
        rb.emplace_back(a[i].first, 0);
        ++i;
      } else {
        ra.emplace_back(a[i++]);
        rb.emplace_back(b[j++]);
      }
    }
    a = ra;
    b = rb;
  }
  long long pow(long long a, int b) {
    long long result = 1;
    while (b > 0) {
      if (b & 1) {
        result *= a;
      }
      a *= a;
      b >>= 1;
    }
    return result;
  }
  long long min_value;
};

　　

code for problem2

#include <algorithm>
#include <iostream>

class FoxAndBusiness {
  public:
    double minimumCost(int K, int totalWork, std::vector<int> a,
        std::vector<int> p) {
      const size_t n = a.size();
      double low = 0.0, high = 1e10;
      for (int i = 0; i < 200; ++i) {
        double mid = (low + high) * 0.5;
        std::vector<double> det(n);
        for (size_t j = 0; j < n; ++j) {
          det[j] = a[j] * (mid - p[j]);
        }
        std::sort(det.rbegin(), det.rend());
        double sum = 0;
        for (int j = 0; j < K; ++j) {
          sum += det[j];
        }
        if (sum >= K * 3600) {
          high = mid;
        } else {
          low = mid;
        }
      }
      return low * totalWork;
    }
};

　　

code for problem3

#include <algorithm>
#include <iostream>
using namespace std;

class FoxAndGreed {
  private:
    static const int MOD = 10007;
    static void Add(int &x, int y) {
      x += y;
      if (x >= MOD) {
        x -= MOD;
      }
    }
  public:
    int count(int H, int W, int S) {
      Init(H, W, S);
      if (std::min(H, W) == 1) {
        return f3[W * H - 1][S];
      }
      int result = 0;
      for (int i = 0; i <= W - 2; ++i) {
        int h = i;
        int v = H - 1;
        int r = W - i - 1;
        Add(result, Binomial(h + v - 1, h) *
            Pow(S + 1, W * H - 1 - h * 2 - v * 2 - r) % MOD *
            Compute(h, v, r, S) % MOD);
      }
      for (int i = 0; i <= H - 2; ++i) {
        int h = W - 1;
        int v = i;
        int r = H - i - 1;
        Add(result, Binomial(h + v - 1, v) *
            Pow(S + 1, W * H - 1 - h * 2 - v * 2 - r) % MOD *
            Compute(h, v, r, S) % MOD);
      }
      return result;
    }
  private:

    int Compute(const int h, const int v, int r, const int S) {
      int result = 0;
      for (int x = 0; x <= S; ++x) {
        for (int y = 0; y + x <= S; ++y) {
          int z = S - x - y;
          Add(result, f1[h][x] * f2[v][y] % MOD * f3[r][z] % MOD);
        }
      }
      return result;
    }

    void Init(const int H, const int W, const int S) {
      auto SetSize = [H, W, S](std::vector<std::vector<int>> &f) {
        f.resize(H + W + 2);
        for (size_t i = 0; i < f.size(); ++i) {
          f[i].resize(S + 1);
        }
      };
      SetSize(f1);
      SetSize(f2);
      SetSize(f3);
      f1[0][0] = f2[0][0] = f3[0][0] = 1;
      for (int i = 1; i <= H + W + 1; ++i) {
        for (int j = 0; j <= S; ++j) {
          f1[i][j] = f2[i][j] = f3[i][j] = 0;
          for (int x = 0; x <= j; ++x) {
            Add(f1[i][j], f1[i - 1][j - x] * (x + 1) % MOD);
            Add(f2[i][j], f2[i - 1][j - x] * x % MOD);
            Add(f3[i][j], f3[i - 1][j - x]);
          }
        }
      }
      fact.resize(H + W + 2);
      invFact.resize(H + W + 2);
      fact[0] = invFact[0] = 1;
      for (size_t i = 1; i < fact.size(); ++i) {
        fact[i] = fact[i - 1] * i % MOD;
        invFact[i] = Pow(fact[i], MOD - 2);
      }
    }

    int Binomial(int n, int m) {
      return fact[n] * invFact[m] % MOD * invFact[n - m] % MOD;
    }

    static int Pow(int a, int b) {
      int r = 1;
      while (b > 0) {
        if (b & 1) {
          r = r * a % MOD;
        }
        a = a * a % MOD;
        b >>= 1;
      }
      return r;
    }

    std::vector<std::vector<int>> f1, f2, f3;
    std::vector<int> fact, invFact;
};