[BZOJ1269]文本编辑器editor

Problem

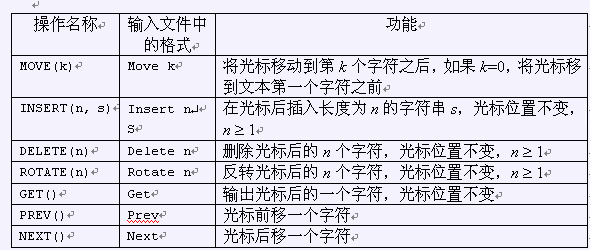
有n个操作

Solution

splay模板题，用splay维护下标。

Notice

需要把l的前一个位置旋转到根，r的后一个位置旋转到根的右节点。所以特别要注意0的大坑。

Code

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define sqz main
#define ll long long
#define reg register int
#define rep(i, a, b) for (reg i = a; i <= b; i++)
#define per(i, a, b) for (reg i = a; i >= b; i--)
#define travel(i, u) for (reg i = head[u]; i; i = edge[i].next)
const int INF = 1e9, N = 2200000;
const double eps = 1e-6, phi = acos(-1);
ll mod(ll a, ll b) {if (a >= b || a < 0) a %= b; if (a < 0) a += b; return a;}
ll read(){ ll x = 0; int zf = 1; char ch; while (ch != '-' && (ch < '0' || ch > '9')) ch = getchar();
if (ch == '-') zf = -1, ch = getchar(); while (ch >= '0' && ch <= '9') x = x * 10 + ch - '0', ch = getchar(); return x * zf;}
void write(ll y) { if (y < 0) putchar('-'), y = -y; if (y > 9) write(y / 10); putchar(y % 10 + '0');}
int point = 0, root, pre, suf, ans, pos = 2;
char st[N + 5];
struct node
{
	char val[N + 5];
	int count[N + 5], son[2][N + 5], parent[N + 5], tag[N + 5];
	inline void up(int u)
	{
		count[u] = count[son[0][u]] + count[son[1][u]] + 1;
	}
	inline void New(int &u, char ch, int last)
	{
		u = ++point;
		parent[u] = last;
		val[u] = ch;
		son[0][u] = son[1][u] = tag[u] = 0;
	}
	inline void change(int u)
	{
		if (u == 0) return;
		tag[u] ^= 1;
		swap(son[0][u], son[1][u]);
	}
	inline void down(int u)
	{
		if (u == 0 || tag[u] == 0) return;
		change(son[0][u]), change(son[1][u]);
		tag[u] = 0;
	}
	inline void build()
	{
		New(root, '~', 0);
		New(son[1][root], '~', root);
		up(root);
	}

	void Rotate(int x, int &rt)
	{
		int y = parent[x], z = parent[y];
		int l = (son[1][y] == x), r = 1 - l;
		if (y == rt) rt = x;
		else if (son[0][z] == y) son[0][z] = x;
		else son[1][z] = x;
		parent[x] = z;
		parent[son[r][x]] = y, son[l][y] = son[r][x];
		parent[y] = x, son[r][x] = y;
		up(y);
		up(x);
	}

	void Splay(int x, int &rt)
	{
		while (x != rt)
		{
			int y = parent[x], z = parent[y];
			if (y != rt)
			{
				if ((son[0][z] == y) ^ (son[0][y] == x))
					Rotate(x, rt);
				else Rotate(y, rt);
			}
			Rotate(x, rt);
		}
	}

	int Find(int u, int x)
	{
		down(u);
		if (x == count[son[0][u]] + 1) return u;
		else if (x <= count[son[0][u]]) return Find(son[0][u], x);
		else return Find(son[1][u], x - count[son[0][u]] - 1);
	}

	void Insert(int &u, int l, int r, int last)
	{
		int mid = (l + r) >> 1;
		New(u, st[mid], last);
		if (l < mid) Insert(son[0][u], l, mid - 1, u);
		if (r > mid) Insert(son[1][u], mid + 1, r, u);
		up(u);
	}

	void adjust(int l, int r)
	{
		int x = Find(root, l - 1), y = Find(root, r + 1);
		Splay(x, root), Splay(y, son[1][root]);
	}

	void solve1()
	{
		int t = read();
		adjust(pos, pos - 1);
		gets(st);
		Insert(son[0][son[1][root]], 0, t - 1, son[1][root]);
		up(son[1][root]), up(root);
	}

	void solve2()
	{
		int t = read();
		adjust(pos, pos + t - 1);
		parent[son[0][son[1][root]]] = 0, son[0][son[1][root]] = 0;
		up(son[1][root]), up(root);
	}

	void solve3()
	{
		int t = read();
		adjust(pos, pos + t - 1);
		change(son[0][son[1][root]]);
	}

	void solve4()
	{
		int t = Find(root, pos);
		printf("%c\n", val[t]);
	}
}Splay_tree;
int sqz()
{
	Splay_tree.build();
	int H_H = read();
	char op[10];
	while(H_H--)
	{
		scanf("%s", op);
		if (op[0] == 'I') Splay_tree.solve1();
		else if (op[0] == 'M') pos = read() + 2;
		else if (op[0] == 'P') --pos;
		else if (op[0] == 'N') ++pos;
		else if (op[0] == 'D') Splay_tree.solve2();
		else if (op[0] == 'R') Splay_tree.solve3();
		else Splay_tree.solve4();
	}
	return 0;
}