Educational Codeforces Round 49 (Rated for Div. 2)A到C题

A题意

给你t表示有t组测试数据，每组数据给你一个含小写字母的字符串，每个字符必须变为它相邻的字符，问最后是否能变成回文串。a不能变成z,反过来也不行

分析

只需对对称位置判断差是否小于2且不等于1，因为等于1无论怎么变都不行

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
    int t;
    int i,n;
    string s;
    //freopen("in.txt","r",stdin);
    while(cin>>t){
    	while(t--){
    		cin>>n>>s;
    		bool flag=1;
    		for(i=0;i<n/2;i++){
    			if(abs(int(s[i]-s[n-(i+1)]))>2||abs(int(s[i]-s[n-(i+1)]))==1)
    			{
				flag=0;
				break;
			}
		}
		if(flag) cout<<"YES\n";
		else cout<<"NO\n";
	}
}
	return 0;
}

B题题意

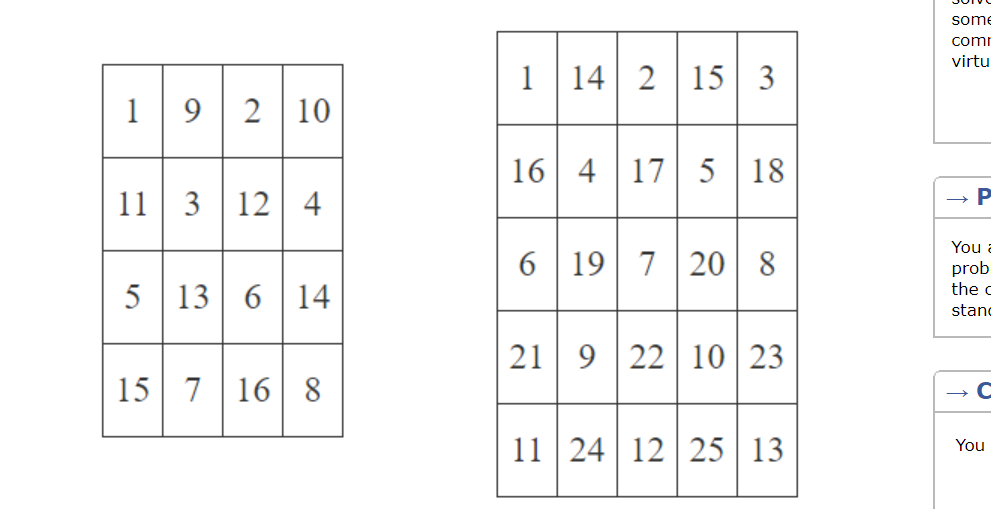
分析

找规律，也不知道怎么说了，注意n奇偶问题

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	ll n,q,x,y;
	//freopen("in.txt","r",stdin);
	while(cin>>n>>q){
		while(q--){
			cin>>x>>y;
			ll ans=0;
			if((x+y)&1){
				ans+=(n*n+1)/2;
				ans+=(y+1)/2;
				ans+=(x-1)/2*n;
				if(x%2==0) ans+=n/2;
			}
			else {
				ans+=(y+1)/2;
				ans+=(x-1)/2*n;
				if(x%2==0) ans+=(n+1)/2;//巧妙处理奇偶问题，很关键
			}
			cout<<ans<<endl;
		}
	}
	return 0;
}

C题题意

给你n个数让你选四个数使构成矩形，使得P*P/S最小，P是周长，S是面积

分析

假设选的是a a b b 那么PP/S==8+4（b/a+a/b）很容易知道当a和b很“近”时，即（b-a）/a越小结果越小

细节就是两两取相等的数，并用另一个数组存c起来，最后排序c,往后比较就好了

还要注意数组清0不要用memset,容易TLE

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
int a[1000010],b[1000010],c[1000010];
int main(){
     int n,t;
     ios::sync_with_stdio(false);
     cin.tie(0);
     cout.tie(0);
    //freopen("in.txt","r",stdin);
     cin>>t;
     	while(t--){
     		cin>>n;
     		int h=0,k;
     		for(int i=0;i<n;i++)
     		{
     			cin>>a[i];
     			b[a[i]]++;
     			if(b[a[i]]==2) c[h++]=a[i],b[a[i]]=0;
			 }
			 for(int i=0;i<n;i++) b[a[i]]=0;//注意清0，不要用memset
			 sort(c,c+h);
			  double ans=99999;
			 for(int i=1;i<h;i++)
			 {
			 	if((c[i]-c[i-1])*1.0/c[i-1]<ans){
			 		k=i;
			 		ans=(c[i]-c[i-1])*1.0/c[i-1];
				 }
			 }
			 cout<<c[k]<<' '<<c[k]<<' '<<c[k-1]<<' '<<c[k-1]<<' '<<endl;
	 }
	return 0;
}