51Nod 1677 treecnt

一道比较基础的计数题，还是一个常用的单独计算贡献的例子。

首先看题目和范围，暴力枚举肯定是不可行的，而且\(O(n\ logn)\)的算法貌似很难写。

那我们就来想\(O(n)\)的吧，我们单独考虑每一条边的贡献，我们注意到一个重要的性质：

树上任意两点间的最短路径都是唯一确定的。

这个常识吧，所以我们只需要考虑每一条边两边的点在计算时会经过这条边多少次。

我们枚举每一条边，然后可以这样考虑这一条边：

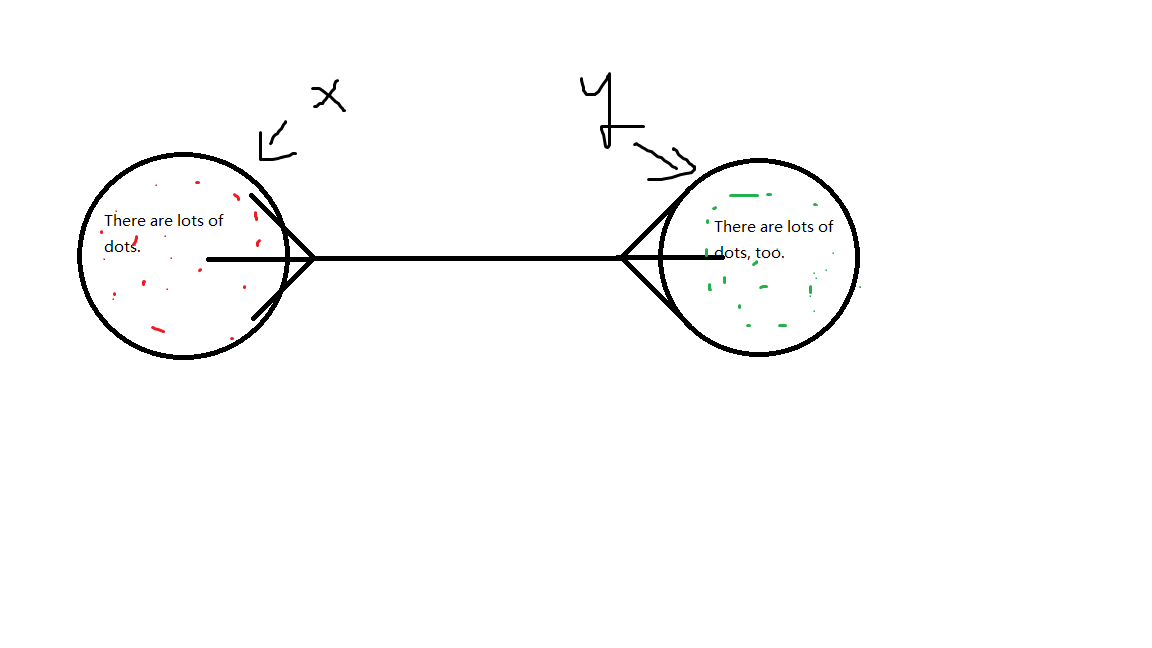
我们设一边有\(x\)个点，另一边有\(y\)个点，很明显\(x+y=n\)

然后我们考虑有多少点之间的路径会经过这条边

用上面的那个性质可以发现，只要在这条边的两边都有点时就满足条件。

然后我们容斥一下就知道答案为：\(C_n^k-C_x^k-C_y^k\)

再注意一下在本题中我们规定当\(a>b\)时\(C_b^a=0\)

关于那个每一条边两边的点数，我们DFS预处理一遍后得到一边的点数，然后根据上面讲的减一下得出另一边的点数即可。

CODE

#include<cstdio>
#include<cstring>
#include<cctype>
const int N=100005,mod=1e9+7;
struct edge
{
	int to,next;
}e[N<<1];
int head[N],fac[N],n,x,y,ans,k,cnt,rt=1,tot,size[N],inv[N];
inline char tc(void)
{
	static char fl[100000],*A=fl,*B=fl;
	return A==B&&(B=(A=fl)+fread(fl,1,100000,stdin),A==B)?EOF:*A++;
}
inline void read(int &x)
{
	x=0; char ch; while (!isdigit(ch=tc()));
	while (x=(x<<3)+(x<<1)+ch-'0',isdigit(ch=tc()));
}
inline void double_add(int x,int y)
{
	e[++cnt].to=y; e[cnt].next=head[x]; head[x]=cnt;
	e[++cnt].to=x; e[cnt].next=head[y]; head[y]=cnt;
}
inline int quick_pow(int x,int p)
{
	int tot=1;
	while (p)
	{
		if (p&1) tot=1LL*tot*x%mod;
		x=1LL*x*x%mod; p>>=1;
	}
	return tot;
}
inline int C(int n,int k)
{
	if (n<k) return 0; if (n==k) return 1;
	return 1LL*fac[n]*inv[k]%mod*inv[n-k]%mod;
}
inline void DFS(int now,int fa)
{
	register int i; size[now]=1;
	for (i=head[now];~i;i=e[i].next)
	if (e[i].to!=fa) DFS(e[i].to,now),size[now]+=size[e[i].to];
}
int main()
{
	//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
	register int i; read(n); read(k);
	memset(head,-1,sizeof(head));
	for (fac[1]=inv[1]=1,i=2;i<=n;++i)
	fac[i]=1LL*fac[i-1]*i%mod,inv[i]=quick_pow(fac[i],mod-2);
	for (i=1;i<n;++i)
	read(x),read(y),double_add(x,y);
	DFS(rt,-1); tot=C(n,k);
	for (i=1;i<=n;++i)
	ans=((1LL*ans+tot-C(size[i],k)+mod)%mod-C(n-size[i],k)+mod)%mod;
	return printf("%d",ans),0;
}