解答：如图

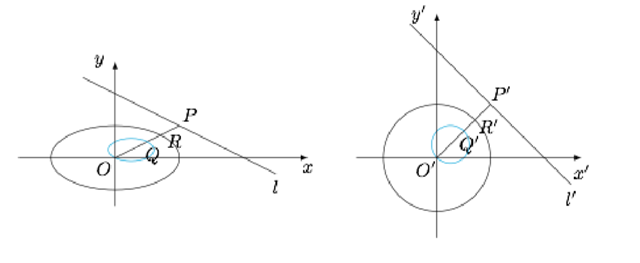
评:1.反演圆及其性质介绍：

评2:此题的源头是1995年全国卷压轴题，这里用极线极点的相关性质也可以处理：

注：用相关点法很容易得到轨迹.

MT【58】反演圆和极线极点和谐统一的更多相关文章

  1. 【资料总结】html开发小实例

    目 录 第1章 1 HTML的基本标签 1 第2章 25 表格基础 25 第3章 53 表单和框架 53 第4章 77 CSS样式表 77 第5章 104 使用Dreamweaver制作网页 104 ...

  2. Excel催化剂图表系列之品味IBCS瀑布图观察企业利润构成

    IBCS图表,每个细节都值得反复琢磨参悟,此篇给大家送上详尽的瀑布图方式下的利润数据观察.请不要拿Excel2016版提供的瀑布图与IBCS版的瀑布图作对比,那完全不是一个级别的,可以类比为拿一辆经济 ...

  3. 豪情-CSS解构系列之-新浪页面解构-02

    前言 一.开发工具 - 前端四大利器 1. WebStorm 1). 岂今为止,业界公认的前端开发利器.优点: 2). 缺点 3). 相关资源 4). 后续展望 2. Photoshop 1).基本信 ...

  4. mmorpg手游中的战斗系统

    目前的项目是一款mmorpg手游, 非常不幸的是,当前战斗系统的实现非常脆弱, 也毫无技巧可言.具体存在如下问题: 1.战斗层逻辑与自动战斗AI逻辑混在一起, 互相纠缠. 2.战斗层自身逻辑混乱不堪, ...

  5. 如何使用office2010插入屏幕截图

    当我们习惯了用QQ的屏幕截图之后,当某一天我们在一台没有装QQ的办公电脑上,它装着office2010,我们可以实现用office来截图吗?其实Office2010深藏着犀利的截图工具. 插入图片到文 ...

  6. 红星美凯龙CEO车建新的圆融和霸气

    待人接物中车建新有许多习惯,与别人一起行走时,走在靠马路的一边:吃饭时最好的菜留给客人.他说,做人往往就在细节中,别小看一个举动,无意中就会感染别人.和别人在一起,你要时时刻刻先考虑对方. 细节上体察 ...

  7. Android 5.x特性概览三

    上节,对Material Design样式做了介绍,这节我们介绍Palette. 在Android发展的长河中,UI越来越成为Google的发展重心.上文提到Android 5.x 使用palette ...

  8. android 5.X之使用Palette

    这几天为了学些android5.0版本sdk的新特性,折腾了好久.AndroidStudio被我反复的安装又卸载又安装,在eclipse和AndroidStudio 之间来回折腾.没想到sdk升级到5 ...

  9. OO之美

    ㈠ 设计的分寸 对于设计,还有很多看似"惯常"的法则与经验广泛存在于软件系统中,例如除了经典的23种设计设计模式.还有很多模式之外的模式,按照粒度的大小,系统的特点,规模的大小,而 ...

随机推荐

  1. sql语句常用功能（null值转换为0）

    COALESCE(规格,' ') 或者 COALESCE(规格,0) select * from ( ) 客户,() 物料号,p4.name 内部批次,p4.outsidename 外部批次,p1.库 ...

  2. c语言学习5

    break 和 continue之间的区别: 在1000人中,募捐100000元,当达到10万元后结束   break 跳出当前循环,即  是终止循环,continue结束本次循环,不终止循环 #in ...

  3. （11）学习笔记 ） ASP.NET CORE微服务 Micro-Service ---- Thrift高效通讯 （完结）

    一. 什么是 RPC Restful 采用 Http 进行通讯,优点是开放.标准.简单.兼容性升级容易: 缺点是性能略低.在 QPS 高或者对响应时间要求苛刻的服务上,可以用 RPC(Remote P ...

  4. SCRUM 12.22

    周一,大家现在课程也比较少,今天都在非常努力地写代码. 任务分配如往常一样,我们现在基本将工作的重心放在完善已有的组件上. 成员 任务 彭林江 落实API 牛强 落实意见反馈功能测试 高雅智 测试已完 ...

  5. Linux内核分析 读书笔记 （第十八章）

    第十八章 调试 18.1 准备开始 1. 需要的只是: 一个bug 一个藏匿bug的内核版本 相关内核代码的知识和运气 2. 在跟踪bug的时候,掌握的信息越多越好. 18.2 内核中的bug 1.  ...

  6. github个人作业

    信息学院本科生课程设计 题目                    文件加密和解密 课程名称 面向对象程序设计课程设计 课程编号 X031749 所在专业 计算机科学与技术 所在班级 计科高职13-3 ...

  7. Service Fabric

    Service Fabric 开源 微软的Azure Service Fabric的官方博客在3.24日发布了一篇博客 Service Fabric .NET SDK goes open source ...

  8. NoSuchBeanDefinitionException：No qualifying bean of type

    Exception in thread "main" org.springframework.beans.factory.NoSuchBeanDefinitionException ...

  9. Beta阶段敏捷冲刺二

    一.举行站立式会议 1.当天站立式会议照片一张 2.团队成员报告 林楚虹 (1) 昨天已完成的工作:连接上数据库 (2) 今天计划完成的工作:修改学习界面单词获取 (3) 工作中遇到的困难:虽然前天询 ...

  10. realm vs. domain

    从wiki的角度:https://wikidiff.com/domain/realm domain是物理的,realm是抽象的,都是领域. domain是一个人或组织拥有或控制的地理区域,而realm ...