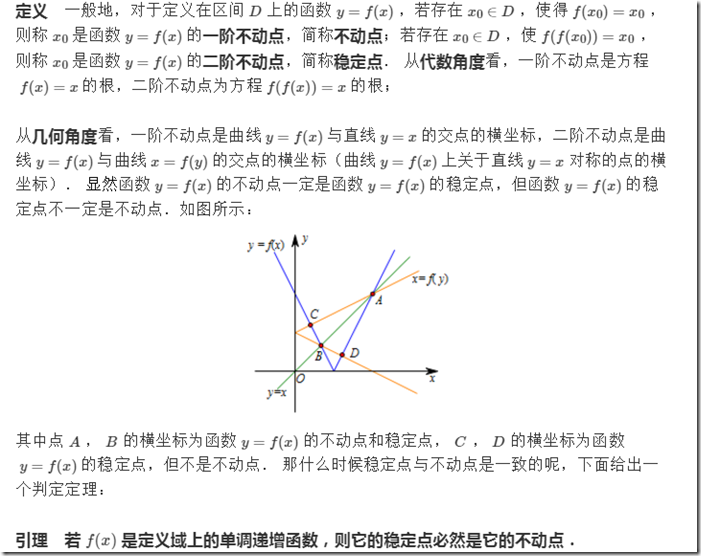
评：不动点概念在数列的一类题中也是非常有用的。

MT【46】不动点，稳定点几何直观的更多相关文章

  1. 非线性方程(组)：一维非线性方程（一）二分法、不动点迭代、牛顿法 [MATLAB]

    1. 二分法(Bisection) 1) 原理 [介值定理] 对于连续的一元非线性函数,若其在两个点的取值异号,则在两点间必定存在零点. [迭代流程] 若左右两端取值不同,则取其中点,求其函数值,取中 ...

  2. 线代笔记 #01# 几何水平上的理解 VS. 数值水平上的理解

    源: 线性代数的本质 内容来自字幕. Let me quote without further comment from Dieudonné's "Foundations of Modern ...

  3. PCA 最大方差理论的直观解释

    PCA 这个名字看起来比较玄乎,其实就是给数据换一个坐标系,然后非常生硬地去掉一些方差很小的坐标轴. 例:三维空间中,有一些数据只分布在一个平面上,我们通过"坐标系旋转变换",使得 ...

  4. Discrete.Differential.Geometry-An.Applied.Introduction(sig2013) 笔记

    The author has a course on web: http://brickisland.net/DDGSpring2016/ It has more reading assignment ...

  5. 支持向量机通俗导论（理解SVM的三层境界）

    原文链接:http://blog.csdn.net/v_july_v/article/details/7624837 作者:July.pluskid :致谢:白石.JerryLead 出处:结构之法算 ...

  6. paper 5：支持向量机系列二: Support Vector —— 介绍支持向量机目标函数的 dual 优化推导，并得出“支持向量”的概念。

    paper 4中介绍了支持向量机,结果说到 Maximum Margin Classifier ,到最后都没有说“支持向量”到底是什么东西.不妨回忆一下上次最后一张图: 可以看到两个支撑着中间的 ga ...

  7. 谢启鸿谈"如何学好高等代数"

    高等代数和数学分析.空间解析几何一起,并称为数学系本科生的三大基础课.所谓基础课,顾名思义,就是本科四年学习的所有数学课程,都是以上述三门课作为基础的.因此对一年级新生而言,学好这三门基础课,其重要性 ...

  8. SVM(支持向量机)算法

    第一步.初步了解SVM 1.0.什么是支持向量机SVM 要明白什么是SVM,便得从分类说起. 分类作为数据挖掘领域中一项非常重要的任务,它的目的是学会一个分类函数或分类模型(或者叫做分类器),而支持向 ...

  9. 开博近一年的感想 by 程序员小白

    /* 好吧,这里的写博客应该理解为更宏观的写文章. */   在去年的这个时候,我所知道的平台只有 CSDN 和博客园..然而 CSDN 的广告实在是不想吐槽了,选择博客园是一件非常自然的事情.要说开 ...

随机推荐

  1. c语言程序设计 第一例子

    #include <studio.h> int main(){ printf("this is  dog.\n"); return 0; } studio.h 表示st ...

  2. 实现Repeater控件的记录单选(二)

    前一篇<实现Repeater控件的记录单选>http://www.cnblogs.com/insus/p/7426334.html 虽然可以实现对Repeater控件的记录进行单选,但是, ...

  3. WPF 任务栏背景闪烁提醒

    原文:WPF 任务栏图标闪烁提醒   public static class FlashWindow { [DllImport("user32.dll")] [return: Ma ...

  4. 机器学习 第四篇：OLS回归分析

    变量之间存在着相关关系,比如,人的身高和体重之间存在着关系,一般来说,人高一些,体重要重一些,身高和体重之间存在的是不确定性的相关关系.回归分析是研究相关关系的一种数学工具,它能帮助我们从一个变量的取 ...

  5. SQL调优日记--并行等待的原理和问题排查

    概述 今天处理项目,客户反应数据库在某个时间段,反应特别慢.需要我们提供一些优化建议. 现象 由于是特定的时间段慢,排查起来就比较方便.直接查看这个时间段数据库的等待情况.查看等待类型发现了大量的CX ...

  6. HTML-JS 数组 内置对象

    [JS中的数组] 1.数组的基本概念? 数组是在内存空间中连续存储的一组有序数据的集合 元素在数组中的顺序,称为下标.可以使用下标访问数组的每个元素 2.如何声明一个数组 ① 使用字面量声明:var ...

  7. 基于HTML5 Canvas WebGL制作分离摩托车

    工业方面制作图表,制作模型方面运用到 3d 模型是非常多的,在一个大的环境中,构建无数个相同的或者不同的模型,构建起来对于程序员来说也是一件相当头疼的事情,我们利用 HT 帮大家解决了很大的难题,无数 ...

  8. ExtJS初探：在项目中使用ExtJS

    注意:本文写作时间是 2013 年,所讲的 ExtJS 如今早已过时,请勿学习! -------------------------------- 今天ExtJS官网发布了ExtJS最新正式版4.2. ...

  9. LVM : 简介

    在对磁盘分区的大小进行规划时,往往不能确定这个分区要使用的空间的大小.而使用 fdisk.gdisk 等工具对磁盘分区后,每个分区的大小就固定了.如果分区设置的过大,就白白浪费了磁盘空间:如果分区设置 ...

  10. SQLServer 中发布与订阅

    在对数据库做迁移的时候,会有很多方法,用存储过程,job,也可以用开源工具kettle,那么今天这些天变接触到了一种新的方法,就是SqlServer中自带的发布与订阅. 首先说明一下数据复制的流程.如 ...