(转)二分图匹配匈牙利算法与KM算法
匈牙利算法转自于: https://blog.csdn.net/dark_scope/article/details/8880547
匈牙利算法是由匈牙利数学家Edmonds于1965年提出,因而得名。匈牙利算法是基于Hall定理中充分性证明的思想,它是部图匹配最常见的算法,该算法的核心就是寻找增广路径,它是一种用增广路径求二分图最大匹配的算法。
-------等等,看得头大?那么请看下面的版本:
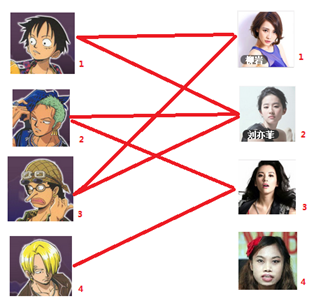
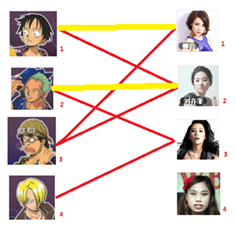
通过数代人的努力,你终于赶上了剩男剩女的大潮,假设你是一位光荣的新世纪媒人,在你的手上有N个剩男,M个剩女,每个人都可能对多名异性有好感( -_-||暂时不考虑特殊的性取向),如果一对男女互有好感,那么你就可以把这一对撮合在一起,现在让我们无视掉所有的单相思(好忧伤的感觉
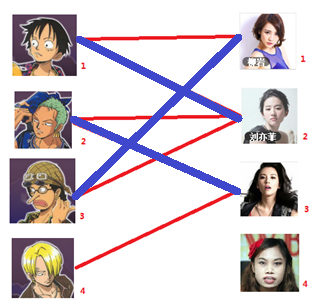
-_-||暂时不考虑特殊的性取向),如果一对男女互有好感,那么你就可以把这一对撮合在一起,现在让我们无视掉所有的单相思(好忧伤的感觉 ),你拥有的大概就是下面这样一张关系图,每一条连线都表示互有好感。
),你拥有的大概就是下面这样一张关系图,每一条连线都表示互有好感。
本着救人一命,胜造七级浮屠的原则,你想要尽可能地撮合更多的情侣,匈牙利算法的工作模式会教你这样做:
===============================================================================
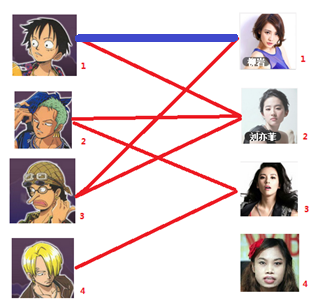
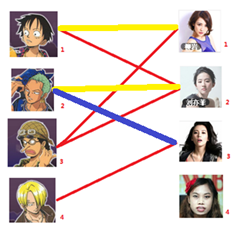
一: 先试着给1号男生找妹子,发现第一个和他相连的1号女生还名花无主,got it,连上一条蓝线
===============================================================================
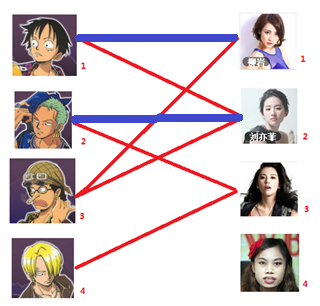
二:接着给2号男生找妹子,发现第一个和他相连的2号女生名花无主,got it
===============================================================================
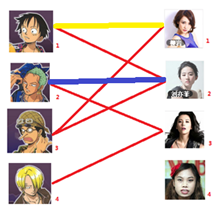
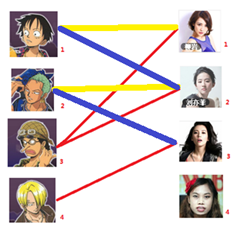
三:接下来是3号男生,很遗憾1号女生已经有主了,怎么办呢?
我们试着给之前1号女生匹配的男生(也就是1号男生)另外分配一个妹子。
(黄色表示这条边被临时拆掉)
与1号男生相连的第二个女生是2号女生,但是2号女生也有主了,怎么办呢?我们再试着给2号女生的原配(
 )重新找个妹子(注意这个步骤和上面是一样的,这是一个递归的过程)
)重新找个妹子(注意这个步骤和上面是一样的,这是一个递归的过程)
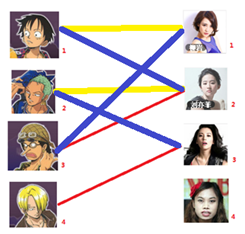
此时发现2号男生还能找到3号女生,那么之前的问题迎刃而解了,回溯回去
2号男生可以找3号妹子~~~ 1号男生可以找2号妹子了~~~ 3号男生可以找1号妹子
所以第三步最后的结果就是:
===============================================================================
四: 接下来是4号男生,很遗憾,按照第三步的节奏我们没法给4号男生腾出来一个妹子,我们实在是无能为力了……香吉士同学走好。
===============================================================================
其原则大概是:有机会上,没机会创造机会也要上
【code】
bool find(int x){
int i,j;
for (j=;j<=m;j++){ //扫描每个妹子
if (line[x][j]==true && used[j]==false)
//如果有暧昧并且还没有标记过(这里标记的意思是这次查找曾试图改变过该妹子的归属问题,但是没有成功,所以就不用瞎费工夫了)
{
used[j]=; //use 用来标记这一个男生想要这一个女生
if (girl[j]== || find(girl[j])) { //名花有主? 那就看看能不能移花接木!
//名花无主或者能腾出个位置来,这里使用递归
girl[j]=x;
return true;
}
}
}
return false;
}
在主程序我们这样做:每一步相当于我们上面描述的一二三四中的一步
for (i=;i<=n;i++) // 遍历每一个男生
{
memset(used,,sizeof(used)); //这个在每一步中清空
if find(i) all+=;
}
KM转载于:https://www.cnblogs.com/logosG/p/logos.html
二、KM算法
现在我们来考虑另外一个问题:如果每个员工做每件工作的效率各不相同,我们如何得到一个最优匹配使得整个公司的工作效率最大呢?

这种问题被称为带权二分图的最优匹配问题,可由KM算法解决。
比如上图,A做工作a的效率为3,做工作c的效率为4......以此类推。
不了解KM算法的人如何解决这个问题?我们只需要用匈牙利算法找到所有的最大匹配,比较每个最大匹配的权重,再选出最大权重的最优匹配即可。这不失为一个解决方案,但是,如果公司员工的数量越来越多,此种算法的实行难度也就越来越大,我们必须另辟蹊径:KM算法。
KM算法解决此题的步骤如下所示:
1.首先对每个顶点赋值,将左边的顶点赋值为最大权重,右边的顶点赋值为0。
如图,我们将顶点A赋值为其两边中较大的4。

2.进行匹配,我们匹配的原则是:只与权重相同的边匹配,若是找不到边匹配,对此条路径的所有左边顶点-1,右边顶点+1,再进行匹配,若还是匹配不到,重复+1和-1操作。(这里看不懂可以跳过,直接看下面的操作,之后再回头来看这里。)
对A进行匹配,符合匹配条件的边只有Ac边。
匹配成功!

接下来我们对B进行匹配,顶点B值为3,Bc边权重为3,匹配成~ 等等,A已经匹配c了,发生了冲突,怎么办?我们这时候第一时间应该想到的是,让B换个工作,但根据匹配原则,只有Bc边 3+0=0 满足要求,于是B不能换边了,那A能不能换边呢?对A来说,也是只有Ac边满足4+0=4的要求,于是A也不能换边,走投无路了,怎么办?

从常识的角度思考:其实我们寻找最优匹配的过程,也就是帮每个员工找到他们工作效率最高的工作,但是,有些工作会冲突,比如现在,B员工和A员工工作c的效率都是最高,这时我们应该让A或者B换一份工作,但是这时候换工作的话我们只能换到降低总体效率值的工作,也就是说,如果令R=左边顶点所有值相加,若发生了冲突,则最终工作效率一定小于R,但是,我们现在只要求最优匹配,所以,如果A换一份工作降低的工作效率比较少的话,我们是能接受的(对B同样如此)。
在KM算法中如何体现呢?
现在参与到这个冲突的顶点是A,B和c,令所有左边顶点值-1,右边顶点值+1,即 A-1,B-1. c+1,结果如下图所示。

我们进行了上述操作后会发现,若是左边有n个顶点参与运算,则右边就有n-1个顶点参与运算,整体效率值下降了1*(n-(n-1))=1,而对于A来说,Ac本来为可匹配的边,现在仍为可匹配边(3+1=4),对于B来说,Bc本来为可匹配的边,现在仍为可匹配的边(2+1=4),我们通过上述操作,为A增加了一条可匹配的边Aa,为B增加了一条可匹配的边Ba。
现在我们再来匹配,对B来说,Ba边 2+0=2,满足条件,所以B换边,a现在为未匹配状态,Ba匹配!

我们现在匹配最后一条边C,Cc 5+1!=5,C边无边能匹配,所以C-1。

现在Cc边 4+1=5,可以匹配,但是c已匹配了,发生冲突,C此时不能换边,于是便去找A,对于A来说,Aa此时也为可匹配边,但是a已匹配,A又去找B。


B现在无边可以匹配了,2+0!=1 ,现在的路径是C→c→A→a→B,所以A-1,B-1,C-1,a+1,c+1。如下图所示。

对于B来说,现在Bb 1+0=1 可匹配!

使用匈牙利算法,对此条路径上的边取反。

如图,便完成了此题的最优匹配。
读者可以发现,这题中冲突一共发生了3次,所以我们一共降低了3次效率值,但是我们每次降低的效率值都是最少的,所以我们完成的仍然是最优匹配!
这就是KM算法的整个过程,整体思路就是:每次都帮一个顶点匹配最大权重边,利用匈牙利算法完成最大匹配,最终我们完成的就是最优匹配!
KM代码:
这个板子是能过的。。。。但竟然过不了uva—1411。。然后 我有找了一个板子。。差不多。。就是用了slack来记录顶标要减小最小值 在下面。。。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <queue>
#include <algorithm>
#include <vector>
#define mem(a, b) memset(a, b, sizeof(a))
using namespace std;
const int maxn = , INF = 0x7fffffff;
int usedx[maxn], usedy[maxn], w[maxn][maxn], bx[maxn], by[maxn], cx[maxn], cy[maxn];
int nx, ny, n, minn, max_value; int dfs(int u)
{
usedx[u] = ;
for(int i=; i<=ny; i++)
{
if(usedy[i] == -)
{
int t = bx[u] + by[i] - w[u][i];
if(t == )
{
usedy[i] = ;
if(cy[i] == - || dfs(cy[i]))
{
cy[i] = u;
cx[u] = i;
return ;
}
}
else if(t > )
minn = min(minn, t);
}
}
return ;
} int km()
{
mem(cx, -);
mem(cy, -);
mem(bx, -);
mem(by, );
for(int i=; i<=nx; i++)
for(int j=; j<=ny; j++)
bx[i] = max(bx[i], w[i][j]);
for(int i=; i<=nx; i++)
{
while() //因为一定可以完美匹配 所以对于每个左边点 找到最大权值匹配再去找下一个点
{
minn = INF;
mem(usedx, -);
mem(usedy, -);
if(dfs(i)) break;
for(int j=; j<=nx; j++) //更新参与到匹配中的左边点和右边点的标值
if(usedx[j] != -) bx[j] -= minn;
for(int j=; j<=ny; j++)
if(usedy[j] != -) by[j] += minn;
}
}
max_value = ;
for(int i=; i<=nx; i++)
if(cx[i] != -)
max_value += w[i][cx[i]];
printf("%d\n",max_value);
} int main()
{
while(~scanf("%d",&n))
{
for(int i=; i<=n; i++)
for(int j=; j<=n; j++)
scanf("%d",&w[i][j]);
nx = ny = n;
km();
}
return ;
}
用这个板子把!
#include <iostream>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <queue>
#include <algorithm>
#include <vector>
#define mem(a, b) memset(a, b, sizeof(a))
using namespace std;
const int maxn = , INF = 0x7fffffff;
int usedx[maxn], usedy[maxn], w[maxn][maxn], bx[maxn], by[maxn], cx[maxn], cy[maxn], slack[maxn];
int nx, ny, n, max_value; int dfs(int u)
{
usedx[u] = ;
for(int i=; i<=ny; i++)
{
if(usedy[i] == -)
{
int t = bx[u] + by[i] - w[u][i];
if(t == )
{
usedy[i] = ;
if(cy[i] == - || dfs(cy[i]))
{
cy[i] = u;
cx[u] = i;
return ;
}
}
else
slack[i] = min(slack[i], t);
}
}
return ;
} void km()
{
mem(cx, -);
mem(cy, -);
mem(bx, -);
mem(by, );
for(int i=; i<=nx; i++)
for(int j=; j<=ny; j++)
bx[i] = max(bx[i], w[i][j]);
for(int i=; i<=nx; i++)
{
for(int j=; j<=n; j++)
slack[j] = INF;
while()
{
mem(usedx, -);
mem(usedy, -);
if(dfs(i)) break;
int d = INF;
for(int j=; j<=ny; j++)
if(usedy[j] == -)
d = min(d, slack[j]);
for(int j=; j<=nx; j++)
if(usedx[j] != -) bx[j] -= d;
for(int j=; j<=ny; j++)
if(usedy[j] != -) by[j] += d;
else
slack[j] -= d;
}
}
max_value = ;
for(int i=; i<=nx; i++)
if(cx[i] != -)
max_value += w[i][cx[i]];
printf("%d\n",max_value);
} int main()
{
while(~scanf("%d", &n))
{
mem(w, 0);
for(int i=; i<=n; i++)
for(int j=; j<=n; j++)
scanf("%d", &w[i][j]);
nx = ny = n;
km();
}
return ;
}
PS:笔者此文旨在用通俗易懂的语言解释匈牙利算法和KM算法,所以对部分定理未加以证明,甚至有的部分一笔带过,这是为了全文的流畅性考虑,不专业之处请多多谅解。
(转)二分图匹配匈牙利算法与KM算法的更多相关文章
- HDU 5943 Kingdom of Obsession 【二分图匹配 匈牙利算法】 (2016年中国大学生程序设计竞赛(杭州))
Kingdom of Obsession Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Oth ...
- USACO 4.2 The Perfect Stall(二分图匹配匈牙利算法)
The Perfect StallHal Burch Farmer John completed his new barn just last week, complete with all the ...
- HDU2255 奔小康赚大钱 (最大权完美匹配) 模板题【KM算法】
<题目链接> 奔小康赚大钱 Problem Description 传说在遥远的地方有一个非常富裕的村落,有一天,村长决定进行制度改革:重新分配房子.这可是一件大事,关系到人民的住房问题啊 ...
- [ZJOI2009]假期的宿舍 二分图匹配匈牙利
[ZJOI2009]假期的宿舍 二分图匹配匈牙利 一个人对应一张床,每个人对床可能不止一种选择,可以猜出是二分图匹配. 床只能由本校的学生提供,而需要床的有住校并且本校和外校两种人.最后统计二分图匹配 ...
- Codevs 1222 信与信封问题 二分图匹配,匈牙利算法
题目: http://codevs.cn/problem/1222/ 1222 信与信封问题 时间限制: 1 s 空间限制: 128000 KB 题目等级 : 钻石 Diamond 题解 ...
- BZOJ1059 [ZJOI2007]矩阵游戏 二分图匹配 匈牙利算法
欢迎访问~原文出处——博客园-zhouzhendong 去博客园看该题解 题目传送门 - BZOJ1059 题意概括 有一个n*n(n<=200)的01矩阵,问你是否可以通过交换整行和整列使得左 ...
- 网络流24题 第三题 - CodeVS1904 洛谷2764 最小路径覆盖问题 有向无环图最小路径覆盖 最大流 二分图匹配 匈牙利算法
欢迎访问~原文出处——博客园-zhouzhendong 去博客园看该题解 题目传送门 - CodeVS1904 题目传送门 - 洛谷2764 题意概括 给出一个有向无环图,现在请你求一些路径,这些路径 ...
- 矩阵游戏|ZJOI2007|BZOJ1059|codevs1433|luoguP1129|二分图匹配|匈牙利算法|Elena
1059: [ZJOI2007]矩阵游戏 Time Limit: 10 Sec Memory Limit: 162 MB Description 小Q是一个非常聪明的孩子,除了国际象棋,他还很喜欢玩 ...
- P2756 飞行员配对方案问题 二分图匹配 匈牙利算法
题目背景 第二次世界大战时期.. 题目描述 英国皇家空军从沦陷国征募了大量外籍飞行员.由皇家空军派出的每一架飞机都需要配备在航行技能和语言上能互相配合的2 名飞行员,其中1 名是英国飞行员,另1名是外 ...
随机推荐
- Vue-Vue列表渲染v-for
v-for 指令需要以 site in sites 形式的特殊语法 一.v-for 循环数组 HTML代码 <div id="app"> <ul> < ...
- odoo订餐系统之菜单设计
1.model类的设计 class MyLunchProduction(osv.Model): _name = "mylunch.production" _description ...
- 2018 Multi-University Training Contest 1 部分简单题解析
Preface ACM系列赛第一站,没有进前200还是很伤的. 主要是T2当时没写出来就GG了,后来看了下其实不是很难. 题目按照比赛时我们A的顺序讲,其实我都是被陈潇然大佬和ZWC带飞的. T1 M ...
- Opencv 2.4.10 +VS2010 项目配置
资料来源:http://blog.csdn.net/scottly1/article/details/40978625
- python中和生成器协程相关的yield之最详最强解释,一看就懂(一)
yield是python中一个非常重要的关键词,所有迭代器都是yield实现的,学习python,如果不把这个yield的意思和用法彻底搞清楚,学习python的生成器,协程和异步io的时候,就会彻底 ...
- Bluedroid 函数分析:bta_dm_gattc_register
我们先来看看在bluedroid 里面有多少地方调用到这里: 可以看出除了 它自己声明的地方,有三处 调用到这个函数. 一处是 进行discovery,一处是进行search的时候,还有一次是bta_ ...
- Qt5.9使用QWebEngineView加载网页速度非常慢,问题解决
折腾了大半天终于解决了 原帖地址:https://bugreports.qt.io/browse/QTBUG-44763 BUG单下的留言讲明了问题发生的原因,那就是系统默认设置为自动寻找代理,而使用 ...
- SpringBoot笔记
官网: http://springboot.fun/ 收集到一个比较全的: https://blog.csdn.net/xiaoyu411502/article/details/52474037 Id ...
- Echarts学习求教
有没有人用过百度的Echarts?刚开始接触,下面这段代码怎么理解啊,新手求指教: myChart.showLoading();$.get('data/asset/data/les-miserable ...
- oracle alter
ALTER TABLE (表名) ADD CONSTRAINT (索引名);ALTER TABLE (表名) DROP CONSTRAINT (索引名); ALTER TABLE (表名) ADD ( ...