POJ 1661 （Help Jimmy ）

Help Jimmy

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 13669		Accepted: 4541

Description

"Help Jimmy" 是在下图所示的场景上完成的游戏。 

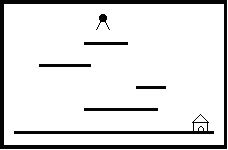
场景中包括多个长度和高度各不相同的平台。地面是最低的平台，高度为零，长度无限。

Jimmy老鼠在时刻0从高于所有平台的某处开始下落，它的下落速度始终为1米/秒。当Jimmy落到某个平台上时，游戏者选择让它向左还是向右跑，它跑动的速度也是1米/秒。当Jimmy跑到平台的边缘时，开始继续下落。Jimmy每次下落的高度不能超过MAX米，不然就会摔死，游戏也会结束。

设计一个程序，计算Jimmy到底地面时可能的最早时间。

Input

第一行是测试数据的组数t（0 <= t <= 20）。每组测试数据的第一行是四个整数N，X，Y，MAX，用空格分隔。N是平台的数目（不包括地面），X和Y是Jimmy开始下落的位置的横竖坐标，MAX是一次下落的最大高度。接下来的N行每行描述一个平台，包括三个整数，X1[i]，X2[i]和H[i]。H[i]表示平台的高度，X1[i]和X2[i]表示平台左右端点的横坐标。1 <= N <= 1000，-20000 <= X, X1[i], X2[i] <= 20000，0 < H[i] < Y <= 20000（i = 1..N）。所有坐标的单位都是米。

Jimmy的大小和平台的厚度均忽略不计。如果Jimmy恰好落在某个平台的边缘，被视为落在平台上。所有的平台均不重叠或相连。测试数据保证问题一定有解。

Output

对输入的每组测试数据，输出一个整数，Jimmy到底地面时可能的最早时间。

Sample Input

1
3 8 17 20
0 10 8
0 10 13
4 14 3

Sample Output23

解析： 用结构体数组存储平台的参数 把起点和地面 也看作平台  然后按照高度排序
题目有两种状态 1、向左走 2、向右走   所以 创建left和right两个函数 （因为需要互相调用  所以要加函数声明） 因为两个函数实现原理相同 所以我们只讨论
一个即可，我们来看left
参数 ans 是当前在的平台 循环是为了找到当前平台下面 挡住老鼠落下的第一个平台 如果没有而且到地面距离又太高 会摔shi的 那么dp【ans】【0】 = INF 即把这个
平台左边到地面所需时间赋为最大值 代表不能通过该左边到达地面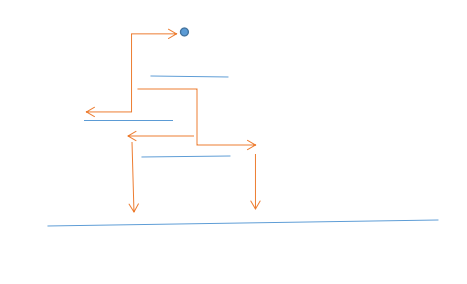

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
using namespace std;
const int maxn = , INF = ;
int T,n,x,y,maxx,dp[maxn][];
int left(int);
int right(int);
struct node{
    int x1,x2,h;
}Node[maxn];

int cmp(node a,node b)
{
    return a.h > b.h;
}

int left(int ans)
{
    if(dp[ans][])
        return dp[ans][];
    if(ans >= n+)
        return ;
    for(int j=ans+; j<=n+; ++j)
    {
        if(Node[j].x1 <= Node[ans].x1 && Node[j].x2 >= Node[ans].x1 && Node[ans].h - Node[j].h <= maxx)
        {
            left(j);
            right(j);
            if(j != n+)
                dp[ans][] = Node[ans].h - Node[j].h + min(dp[j][] + Node[ans].x1 - Node[j].x1, dp[j][] + Node[j].x2 - Node[ans].x1);
            else
                dp[ans][] = Node[ans].h;
            break;
        }
        else
            dp[ans][] = INF;
    }
}

int right(int ans)
{
    if(dp[ans][])
        return dp[ans][];
    if(ans >= n+)
        return ;
    for(int j=ans+; j<=n+; ++j)
    {
        if(Node[j].x1 <= Node[ans].x2 && Node[j].x2 >= Node[ans].x2 && Node[ans].h - Node[j].h <= maxx)
        {
            left(j);
            right(j);
            if(j != n+)
                dp[ans][] = Node[ans].h - Node[j].h + min(dp[j][] + Node[j].x2 - Node[ans].x2, dp[j][] + Node[ans].x2 - Node[j].x1);
            else
                dp[ans][] = Node[ans].h;
            break;

        }
        else
            dp[ans][] = INF;
    }
}

int main()
{
    cin>>T;
    while(T--)
    {
        memset(dp,,sizeof(dp));
        memset(Node,,sizeof(Node));
        cin>>n>>x>>y>>maxx;
        Node[].x1 = Node[].x2 = x; Node[].h = y;    //把起点放进数组
        for(int i=;i<=n;i++)
        {
            cin>>Node[i].x1>>Node[i].x2>>Node[i].h;
        }
        Node[n+].x1 = -; Node[n+].x2 = ; Node[n+].h = ;    //把地面放进数组
        sort(Node,Node+n+,cmp);
//        for(int i=0;i<=n+1;i++)
//            cout<<Node[i].x1<<" "<<Node[i].x2<<" "<<Node[i].h<<endl;
//
        left();
        right();
        cout<<min(dp[][], dp[][])<<endl;
    }

    return ;
}