20231112多校模拟T2

题目描述

给你下列7种形状，问恰好填满 \(n*2\) 的方格有多少种方案（每种形状可任意旋转）

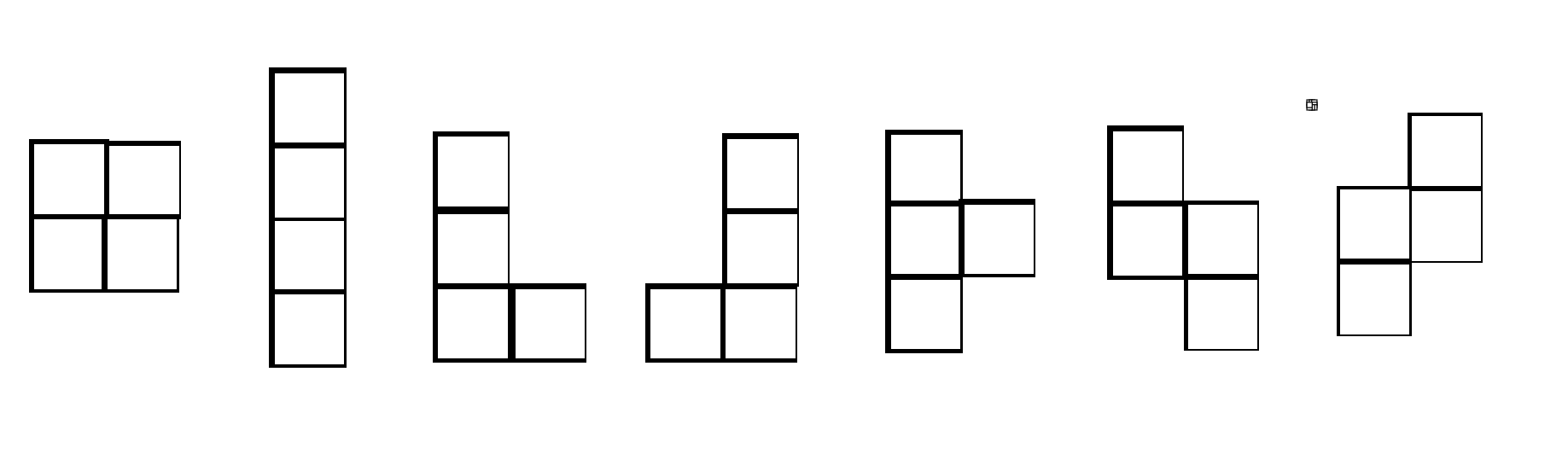
后三种形状纯粹是出题人的恶趣味，d用没有

做法一：暴力

不会

做法二：递推

定义：

• f[i] 为填满 \(i*2\) 的方格的方案数
• g[i] 为填满 \(i*2\) 的方格 不能被腰斩 的方案数

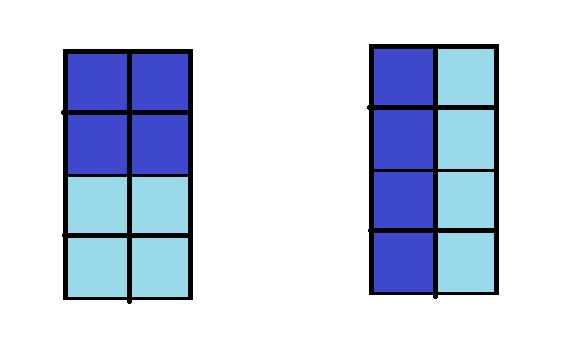
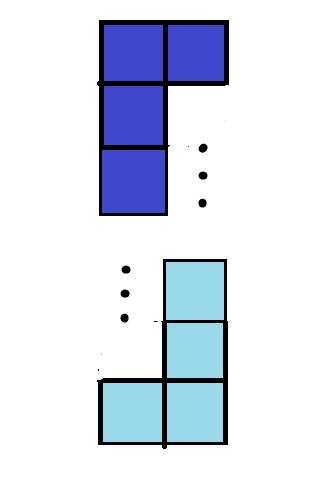
解释：例如当 \(n = 4\) 时，下列第一种画法能被腰斩，第二种不能

初步分析

很容易得到, 当 \(i\) 为奇数时 答案答案显然为0

且

\[f[0] = 1, g[0] = 1, f[2] = 1, g[2] = 1, f[4] = 4, g[4] = 3
\]

当i为大于4的偶数时

\[f[i] = g[i] * f[0] + g[i - 2] * f[2] + g[i - 4] * f[4] + ... + g[2] * f[i - 2]
\]

进一步发现

\[g[i] = 2
\]

解释：上下两端用第3， 第4种方块， 中间用2填满

然后可以得到递推式

\[f[i] = 2 * (f[0] + f[2] + f[4] + ... f[i - 6]) + 3 * f[i - 4] + f[i - 2]
\]

前面一部分可用前缀和优化一下变为：

\[f[i] = 2 * (sum[i - 6]) + 3 * f[i - 4] + f[i - 2]
\]

发现奇数项根本没有用，优化一下空间

\[f[i] = 2 * (sum[i - 3]) + 3 * f[i - 2] + f[i - 1]
\]

此时答案为 \(f[\dfrac{n}{2}]\)

进一步优化

\(O(n)\) 做法跑 \(10^{18}\) 肯定会爆，考虑上述式子用矩阵乘法优化

\[\left[ \begin{matrix}
f[i] \\
f[i - 1] \\
sum[i - 2]
\end{matrix}
\right] =
\left[
\begin{matrix}
1 & 3 & 2\\
1 & 0 & 0\\
0 & 1 & 1
\end{matrix}
\right]
\left[
\begin{matrix}
f[i - 1] \\
f[i - 2] \\
sum[i - 3]
\end{matrix}
\right]

\]

至此，复杂度优化为\(O(logn)\)

AC代码

#include<iostream>
#include<cstring>
#define ll long long

using namespace std;
const ll P = 1e9 + 7, N = 2e6;

ll f[3] = {1, 1, 4};
ll sum[3] = {1, 2, 6};
ll n;

void mul(ll a[3][3], ll b[3][3]) {
	ll c[3][3]; memset(c, 0, sizeof c);
	for(int k = 0; k < 3; k ++) {
		for(int i = 0; i < 3; ++ i)
			for(int j = 0; j < 3; ++ j)
				c[i][j] = (c[i][j] + a[i][k] * b[k][j]) % P;
	}
	memcpy(a, c, sizeof c);
}

ll q_pow(ll b) {
	if(b < 3) return f[b];
	ll ret[3][3] = {1, 0, 0,    0, 1, 0,    0, 0, 1};
	ll a[3][3] = { 1, 3, 2,    1, 0, 0,    0, 1, 1};

	++ b;
	while(b) {
		if(b & 1) mul(ret, a);
		mul(a, a);
		b >>= 1;
	}
	return ret[1][0];
}

int main() {
	while(scanf("%lld", &n) != EOF) {
		if(n & 1) puts("0");
		else printf("%lld\n", q_pow(n / 2));
	}
	return 0;
}

其他做法

机房大佬说这题就是斐波那契第n项的平方

我太弱了不会推