2022-02-21:不含连续1的非负整数。 给定一个正整数 n ,返回范围在 [0, n] 都非负整数中,其二进制表示不包含 连续的 1 的个数。 输入: n = 5 输出: 5 解释: 下面是带
2022-02-21:不含连续1的非负整数。
给定一个正整数 n ,返回范围在 [0, n] 都非负整数中,其二进制表示不包含 连续的 1 的个数。
输入: n = 5
输出: 5
解释:
下面是带有相应二进制表示的非负整数<= 5:
0 : 0
1 : 1
2 : 10
3 : 11
4 : 100
5 : 101
其中,只有整数3违反规则(有两个连续的1),其他5个满足规则。
1 <= n <= 10的9次方。
力扣600。
答案2022-02-21:
动态规划。
根据规律,跟斐波那契数列有关,但未找到这种解法。
代码用golang编写。代码如下:
package main
import "fmt"
func main() {
n := 15
ret := findIntegers(n)
fmt.Println(ret)
}
func findIntegers(n int) int {
i := 31
for ; i >= 0; i-- {
if (n & (1 << i)) != 0 {
break
}
}
// for循环出来之后,i表示,n最高位的1,在哪?
// 从这个位置,往右边低位上走!
dp := make([][][]int, 2)
for ii := 0; ii < 2; ii++ {
dp[ii] = make([][]int, 2)
for j := 0; j < 2; j++ {
dp[ii][j] = make([]int, i+2)
}
}
return f(0, 0, i, n, dp)
}
func f(pre, alreadyLess, index, num int, dp [][][]int) int {
if index == -1 {
return 1
}
if dp[pre][alreadyLess][index] != 0 {
return dp[pre][alreadyLess][index]
}
ans := 0
if pre == 1 {
ans = f(0, getMax(alreadyLess, twoSelectOne((num&(1<<index)) != 0, 1, 0)), index-1, num, dp)
} else {
if (num&(1<<index)) == 0 && alreadyLess == 0 {
ans = f(0, alreadyLess, index-1, num, dp)
} else {
ans = f(1, alreadyLess, index-1, num, dp) + f(0, getMax(alreadyLess, twoSelectOne((num&(1<<index)) != 0, 1, 0)), index-1, num, dp)
}
}
dp[pre][alreadyLess][index] = ans
return ans
}
func getMax(a, b int) int {
if a > b {
return a
} else {
return b
}
}
func twoSelectOne(c bool, a, b int) int {
if c {
return a
} else {
return b
}
}
执行结果如下:
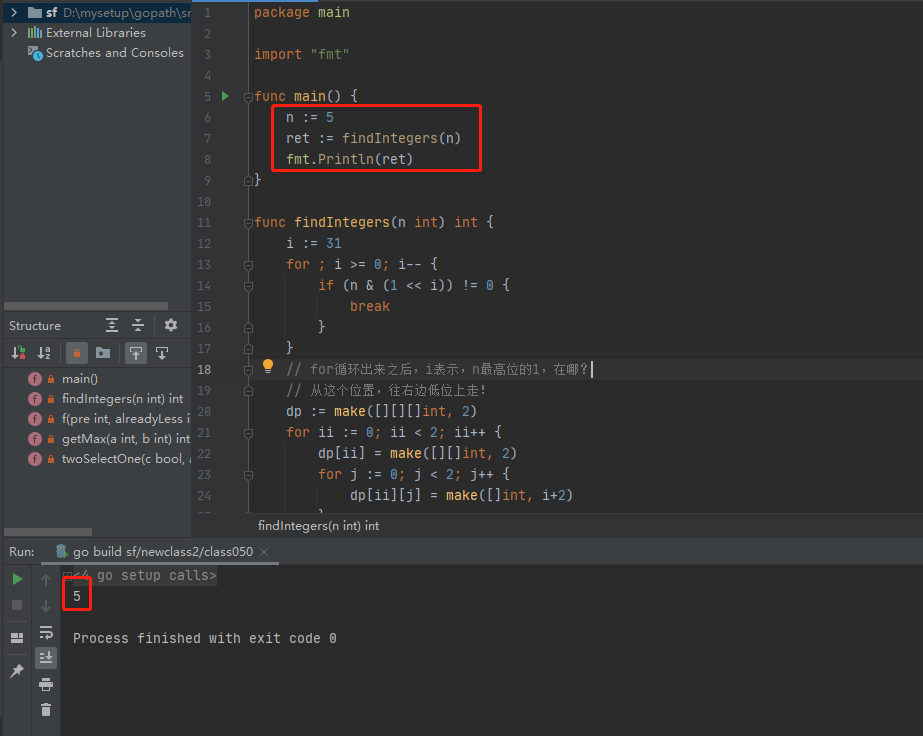
2022-02-21:不含连续1的非负整数。 给定一个正整数 n ,返回范围在 [0, n] 都非负整数中,其二进制表示不包含 连续的 1 的个数。 输入: n = 5 输出: 5 解释: 下面是带的更多相关文章
- 输入一个正整数n,计算出[0,n]这些整数中的二进制数没有连续3个1的数字有多少
输入一个正整数n,计算出[0,n]这些整数中的二进制数没有连续3个1的数字有多少? 例子:输入数字9,则输出结果位9.因为[0-9]中,只有数字7有连续的三个‘1’出现,别的都没有,所以一共有9个数字 ...
- 2022.02.21 UB
2022.02.21 UB 参考资料: https://zhuanlan.zhihu.com/p/141467895 https://blog.csdn.net/ghscarecrow/article ...
- 2022.02.21 SA
2022.02.21 SA 当我年少轻狂时,我曾拥有自由,但我并不明白它的意义.我曾拥有时间,但我没有意识到它的珍贵.我曾拥有爱,但我从未用心去体会.数十年的时间考验后,我终于理解了三者的真谛. 我已 ...
- c#编程:给定一个正整数求出是几位数并逆序输出
<span style="color:#FF0000;">第一步:把输入的数字转为字符串n.ToString() 第二步:求出字符串的长度即为正整数的位数 第三步:从后 ...
- 4.给定一个正整数m,统计m的位数,分别打印每一位数字,再按照逆序打印出各位数字。 要求:m定义为类的属性,需定义构造函数为m赋值;当m大于99999时,输出错误信息“the number is too large”,不再执行。
package a; public class ShuZi { int m; public int getM() { return m; } public void setM(int m) { thi ...
- Leetcode 600.不包含连续1的非负整数
不包含连续1的非负整数 给定一个正整数 n,找出小于或等于 n 的非负整数中,其二进制表示不包含 连续的1 的个数. 示例 1: 输入: 5 输出: 5 解释: 下面是带有相应二进制表示的非负整数&l ...
- [2017.02.21] 《Haskell趣学指南 —— Learning You a Haskell for Great Good!》
{- 2017.02.21 <Haskell趣学指南 -- Learning You a Haskell for Great Good!> [官网](http://learnyouahas ...
- FFMpeg ver 20160219-git-98a0053 滤镜中英文对照 2016.02.21 by 1CM
FFMpeg ver 20160219-git-98a0053 滤镜中英文对照 2016.02.21 by 1CM T.. = Timeline support 支持时间轴 .S. = Slice t ...
- ab输出信息解释以及Failed requests原因分析
ab是apache自带的压力测试工具.ab进行的一切测试本质上是基于HTTP的.下面是对ab输出项信息的解释和出现Failed requests原因分析.测试实例:1. ab输出信息说明: 1 2 ...
- ThinkPHP模版引擎之变量输出具体解释
ThinkPHP模版引擎之变量输出具体解释 使用ThinkPHP开发有一定时间了,今日对ThinkPHP的模板引擎变量解析深入了解了一下.做出一些总结,分享给大家供大家參考. 详细分析例如以下: 我们 ...
随机推荐
- 行转列 && 字段拆分
explode称之为Hive爆炸函数,意思就是将一行数据炸开.Usage:explode(array/map) explode函数传递的参数必须是一个array或者是map hivescala> ...
- C#重点语法——特性
特性的基本理解 ************************************************************************************* 一.含义 特 ...
- 文本的格式化标签(粗体,斜体)和 <div>和<span>标签(都是双标签)
上一个笔记有提到各种型号的标题,为了保证文章的美观,又会有除了标题之外的东西,比如粗体,斜体,下划线,删除线和各种分隔 1加粗,<strong><strong/>或者<b ...
- python内置函数len()
len() len()函数用于返回对象(字符串.元组.列表和字典等)的长度或元素个数 len()函数的语法: len(s) 代码示例 print(len(range(10))) print(len([ ...
- 解决Selenium元素拖拽不生效Bug
转载请注明出处️ 作者:测试蔡坨坨 原文链接:caituotuo.top/e8aa6c6f.html 你好,我是测试蔡坨坨. 前几天在使用Selenium进行元素拖拽操作时,发现Selenium自带的 ...
- Android LineChart 折线图Demo
1 首先在 build.gradle 里导入包 implementation 'com.github.PhilJay:MPAndroidChart:v3.1.0' 2.新建 启动Activity Li ...
- ChatGPT 设计游戏剧情 | 基于 AI 5 天创建一个农场游戏,完结篇!
欢迎使用 AI 进行游戏开发! 在本系列中,我们将使用 AI 工具在 5 天内创建一个功能完备的农场游戏.到本系列结束时,您将了解到如何将多种 AI 工具整合到游戏开发流程中.本文将向您展示如何将 A ...
- 我用ChatGPT做WebRTC音视频性能优化,主打一个高效
摘要 随着GPT-4的发布,AI的风越吹越旺.GPT-4可以回答问题,可以写作,甚至可以基于一张草图生成html代码搭建一个网站.即构社区的一位开发者@倪同学就基于目前在研究的WebRTC QOS技术 ...
- WebSocket集群解决方案,不用MQ
首先不了解WebSocket的可以先看看这篇文章,以及传统的WebSocket方案是怎么做的,https://www.cnblogs.com/jeremylai7/p/16875115.html ...
- 保持唯一性,请停止使用【python3 内置hash() 函数】
问题: 如图,用hash() 筛重时竟然出现了重复. 如下图: hash字符串时,同一窗口的是一致的,不同窗口结果竟然不同. 原因: python的字符串hash算法并不是直接遍历字符串每个字符去计算 ...
