P8575 「DTOI-2」星之河 题解
题目链接：星之河
比较经典的偏序问题。区别于强制在线类算法：树套树之类的，对于偏序问题，我们有许多种优秀的离线算法，比如此篇要讲的 cdq 分治。
它更偏向于一种思想，它的思想使得它对偏序类问题，往往都有一种非常好的效果。首先来看一张图。
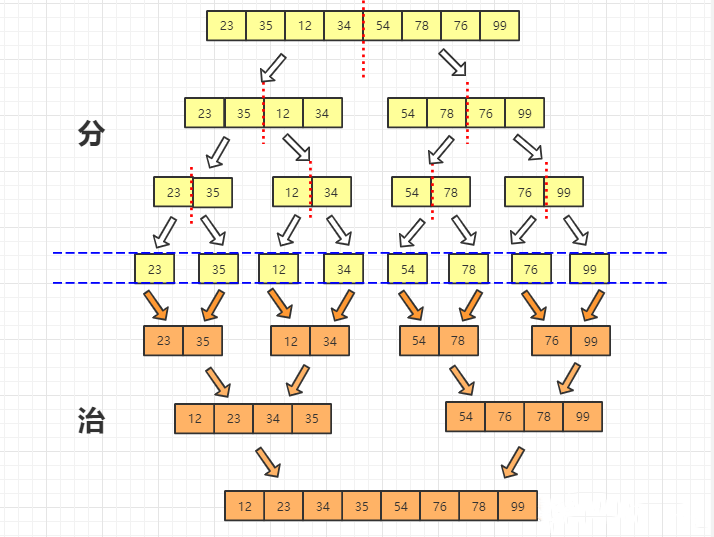
这是所有算法入门选手都会接触的归并排序的过程图。我们考虑两个过程，一个是向下不断分解到小区间，最终长度为 \(1\) 的区间开始往上合并。容易发现，对于排序类问题，我们常常来说可以至少优化掉一维，比如对第一维进行有序排序。那么很容易观察到此时此刻的两个需要合并的区间： \([l,mid]\) 与 \([mid+1,r]\) 它们之间有一个很明显的关系，那就是第一维因为是有序的，那么左区间的所有的第一维一定是 \(\le\) 右区间的第一维的。此时此刻，我们可以考虑左区间对右区间的贡献，考虑完毕以后，他们组成了新的：
- 左区间对下一个右区间作为贡献。
- 右区间统计其他左区间对它的贡献。
这个就是 cdq 分治的核心思想：在归并的过程中，统计左区间对右区间的影响即可。偏序类问题常常都是一个方向的，例如 \(x_i \le x_j \ (i<j)\)，只需要考虑 \(i\) 对 \(j\) 的贡献即可，也就是左边的点对右边的点的贡献性，很符合 cdq 分治模型。
三维偏序从暴力到正解
考虑枚举右区间的每个端点，暴力地统计每个点剩下两维是否能对当前点造成贡献，这个复杂度显然是很高的。考虑优化，我们如果左右区间的第二维在自身的区间内是有序的，那么很显然我们可以用双指针算法，很容易的找到对于右区间的某个点应该有左区间哪部分影响到。这部分本质上抽象出来就是这么个东西：
\]
这个很简单吧，跑双指针轻松实现。那么第二维我们就可以去掉了，最后就是一个很简单的贡献区域查询。比如我们将 \(1 \sim left_i\) 对应的第三维加入贡献中，考虑当前点 \(right_i\) 需要的贡献范围就行了，带修的数据结构都行。基础树状数组比较常用。
来解决下如何让第二维有序，别忘了我们本质上的结构是“归并排序”，归并排序的核心操作就是在归并时完成：
\]
当然了，实际情景如果懒得写这个 \(merge\) 可以考虑直接调稳定排序的函数，因为基本接近有序了，这部分常数并不是很大。对此，我们的三维偏序就暂时讲到这。
本题核心转化，对于一个子树类型的题，我们常常会使用 dfs 序将其转化为区间上的问题，容易知道，处理出一个 dfs序 以后，很容易通过区间查找 \([s_{curr},e_{curr}]\) 找出这部分的贡献。我们常见的计数类型题可以考虑用树状数组前缀和做差实现。
那么核心点就是处理出 dfs 序以后转化为这样一个问题：
对于两个点 \(i\) 与 \(j\):
- \(A_i \le A_j\)
- \(B_i \le B_j\)
- \(s_{i} \le s_j \le e_i，其中s_i 是dfs序起点，e_i则是终点\)
那么很显然的一个 cdq 分治求偏序问题。
最后的细节
首先呢，怎么处理 dfs 序因个人而已，有人喜欢终点也加一，那么对应的查询范围也需要有所更改。
其次呢，对于 cdq 分治而言，最容易错的地方，莫过于考虑当相等时该如何排序了。这点是必须去具体考虑的。例如本题而言，你要注意到一点，当 \(A_i 和 B_i\) 都相等的两个偏序对，你应该考虑谁对谁的影响，注意 cdq 分治只考虑左边对右边的影响，所以只能一方对一方产生影响。很容易知道，第三维 dfs 序越小的越可能是根，否则如果这两个点是同棵子树，而前者恰好又是根，你还是按照原本的 dfs 序以升序排列，那么很显然，根对子树无影响，漏算了子树对根的影响，所以这里排序记得手写一下。
最后就是有无手写 merge 的两个版本代码，不过其实 c++ 也有自带的 merge 函数可以调用，不过照顾其他语言选手还是手写出来。
无merge参照代码
#include <bits/stdc++.h>
//#pragma GCC optimize("Ofast,unroll-loops")
// #define isPbdsFile
#ifdef isPbdsFile
#include <bits/extc++.h>
#else
#include <ext/pb_ds/priority_queue.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/pb_ds/trie_policy.hpp>
#include <ext/pb_ds/tag_and_trait.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/list_update_policy.hpp>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/exception.hpp>
#include <ext/rope>
#endif
using namespace std;
using namespace __gnu_cxx;
using namespace __gnu_pbds;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef tuple<int, int, int> tii;
typedef tuple<ll, ll, ll> tll;
typedef unsigned int ui;
typedef unsigned long long ull;
typedef __int128 i128;
#define hash1 unordered_map
#define hash2 gp_hash_table
#define hash3 cc_hash_table
#define stdHeap std::priority_queue
#define pbdsHeap __gnu_pbds::priority_queue
#define sortArr(a, n) sort(a+1,a+n+1)
#define all(v) v.begin(),v.end()
#define yes cout<<"YES"
#define no cout<<"NO"
#define Spider ios_base::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
#define MyFile freopen("..\\input.txt", "r", stdin),freopen("..\\output.txt", "w", stdout);
#define forn(i, a, b) for(int i = a; i <= b; i++)
#define forv(i, a, b) for(int i=a;i>=b;i--)
#define ls(x) (x<<1)
#define rs(x) (x<<1|1)
#define endl '\n'
//用于Miller-Rabin
[[maybe_unused]] static int Prime_Number[13] = {0, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};
template <typename T>
int disc(T* a, int n)
{
return unique(a + 1, a + n + 1) - (a + 1);
}
template <typename T>
T lowBit(T x)
{
return x & -x;
}
template <typename T>
T Rand(T l, T r)
{
static mt19937 Rand(time(nullptr));
uniform_int_distribution<T> dis(l, r);
return dis(Rand);
}
template <typename T1, typename T2>
T1 modt(T1 a, T2 b)
{
return (a % b + b) % b;
}
template <typename T1, typename T2, typename T3>
T1 qPow(T1 a, T2 b, T3 c)
{
a %= c;
T1 ans = 1;
for (; b; b >>= 1, (a *= a) %= c)if (b & 1)(ans *= a) %= c;
return modt(ans, c);
}
template <typename T>
void read(T& x)
{
x = 0;
T sign = 1;
char ch = getchar();
while (!isdigit(ch))
{
if (ch == '-')sign = -1;
ch = getchar();
}
while (isdigit(ch))
{
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
x *= sign;
}
template <typename T, typename... U>
void read(T& x, U&... y)
{
read(x);
read(y...);
}
template <typename T>
void write(T x)
{
if (typeid(x) == typeid(char))return;
if (x < 0)x = -x, putchar('-');
if (x > 9)write(x / 10);
putchar(x % 10 ^ 48);
}
template <typename C, typename T, typename... U>
void write(C c, T x, U... y)
{
write(x), putchar(c);
write(c, y...);
}
template <typename T11, typename T22, typename T33>
struct T3
{
T11 one;
T22 tow;
T33 three;
bool operator<(const T3 other) const
{
if (one == other.one)
{
if (tow == other.tow)return three > other.three;
return tow < other.tow;
}
return one < other.one;
}
T3() { one = tow = three = 0; }
T3(T11 one, T22 tow, T33 three) : one(one), tow(tow), three(three)
{
}
};
template <typename T1, typename T2>
void uMax(T1& x, T2 y)
{
if (x < y)x = y;
}
template <typename T1, typename T2>
void uMin(T1& x, T2 y)
{
if (x > y)x = y;
}
constexpr int N = 2e5 + 10;
vector<int> child[N];
int s[N], e[N], tot;
//Ai、Bi、i
T3<int, int, int> t[N];
int siz;
inline void dfs(const int curr, const int fa)
{
s[curr] = ++tot;
for (const auto nxt : child[curr])if (nxt != fa)dfs(nxt, curr);
e[curr] = tot;
}
int n;
int ans[N];
int bit[N];
//注意到需要保留子树对根的影响，子树应该在左边
inline bool cmpA(const T3<int, int, int>& x, const T3<int, int, int> y)
{
if (x.one != y.one)return x.one < y.one;
if (x.tow != y.tow)return x.tow < y.tow;
return s[x.three] > s[y.three];
}
inline bool cmpB(const T3<int, int, int>& x, const T3<int, int, int> y)
{
return x.tow < y.tow;
}
inline void add(int x, const int val)
{
for (; x <= n; x += lowBit(x))bit[x] += val;
}
inline int query(int x)
{
int ans = 0;
for (; x; x -= lowBit(x))ans += bit[x];
return ans;
}
inline int Query(const int l, const int r)
{
return query(r) - query(l - 1);
}
inline void cdq(const int L, const int R)
{
const int mid = L + R >> 1;
if (L == R)return;
cdq(L, mid), cdq(mid + 1, R);
//去掉B的影响
stable_sort(t + L, t + mid + 1, cmpB);
stable_sort(t + mid + 1, t + R + 1, cmpB);
//基本双指针
int l = L;
forn(r, mid+1, R)
{
int queryPoint = t[r].three;
for (; l <= mid and t[l].tow <= t[r].tow; l++)add(s[t[l].three], 1);
ans[queryPoint] += Query(s[queryPoint], e[queryPoint]); //区间查询子树区间贡献
}
//清空用于下次计算
forn(i, L, l-1)add(s[t[i].three], -1);
}
inline void solve()
{
cin >> n;
forn(i, 1, n-1)
{
int u, v;
cin >> u >> v;
child[u].push_back(v);
child[v].push_back(u);
}
dfs(1, 0); //处理dfs序
forn(i, 1, n)
{
auto& [A,B,id] = t[i];
cin >> A >> B, id = i;
}
//去掉A的影响
sort(t + 1, t + n + 1, cmpA);
cdq(1, n);
forn(i, 1, n)if (ans[i])cout << ans[i] << endl;
}
signed int main()
{
Spider
//------------------------------------------------------
int test = 1;
// read(test);
// cin >> test;
forn(i, 1, test)solve();
// while (cin >> n, n)solve();
// while (cin >> test)solve();
}
有merge参照代码
#include <bits/stdc++.h>
//#pragma GCC optimize("Ofast,unroll-loops")
// #define isPbdsFile
#ifdef isPbdsFile
#include <bits/extc++.h>
#else
#include <ext/pb_ds/priority_queue.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/tree_policy.hpp>
#include <ext/pb_ds/trie_policy.hpp>
#include <ext/pb_ds/tag_and_trait.hpp>
#include <ext/pb_ds/hash_policy.hpp>
#include <ext/pb_ds/list_update_policy.hpp>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/exception.hpp>
#include <ext/rope>
#endif
using namespace std;
using namespace __gnu_cxx;
using namespace __gnu_pbds;
typedef long long ll;
typedef long double ld;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef tuple<int, int, int> tii;
typedef tuple<ll, ll, ll> tll;
typedef unsigned int ui;
typedef unsigned long long ull;
typedef __int128 i128;
#define hash1 unordered_map
#define hash2 gp_hash_table
#define hash3 cc_hash_table
#define stdHeap std::priority_queue
#define pbdsHeap __gnu_pbds::priority_queue
#define sortArr(a, n) sort(a+1,a+n+1)
#define all(v) v.begin(),v.end()
#define yes cout<<"YES"
#define no cout<<"NO"
#define Spider ios_base::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
#define MyFile freopen("..\\input.txt", "r", stdin),freopen("..\\output.txt", "w", stdout);
#define forn(i, a, b) for(int i = a; i <= b; i++)
#define forv(i, a, b) for(int i=a;i>=b;i--)
#define ls(x) (x<<1)
#define rs(x) (x<<1|1)
#define endl '\n'
//用于Miller-Rabin
[[maybe_unused]] static int Prime_Number[13] = {0, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};
template <typename T>
int disc(T* a, int n)
{
return unique(a + 1, a + n + 1) - (a + 1);
}
template <typename T>
T lowBit(T x)
{
return x & -x;
}
template <typename T>
T Rand(T l, T r)
{
static mt19937 Rand(time(nullptr));
uniform_int_distribution<T> dis(l, r);
return dis(Rand);
}
template <typename T1, typename T2>
T1 modt(T1 a, T2 b)
{
return (a % b + b) % b;
}
template <typename T1, typename T2, typename T3>
T1 qPow(T1 a, T2 b, T3 c)
{
a %= c;
T1 ans = 1;
for (; b; b >>= 1, (a *= a) %= c)if (b & 1)(ans *= a) %= c;
return modt(ans, c);
}
template <typename T>
void read(T& x)
{
x = 0;
T sign = 1;
char ch = getchar();
while (!isdigit(ch))
{
if (ch == '-')sign = -1;
ch = getchar();
}
while (isdigit(ch))
{
x = (x << 3) + (x << 1) + (ch ^ 48);
ch = getchar();
}
x *= sign;
}
template <typename T, typename... U>
void read(T& x, U&... y)
{
read(x);
read(y...);
}
template <typename T>
void write(T x)
{
if (typeid(x) == typeid(char))return;
if (x < 0)x = -x, putchar('-');
if (x > 9)write(x / 10);
putchar(x % 10 ^ 48);
}
template <typename C, typename T, typename... U>
void write(C c, T x, U... y)
{
write(x), putchar(c);
write(c, y...);
}
template <typename T11, typename T22, typename T33>
struct T3
{
T11 one;
T22 tow;
T33 three;
bool operator<(const T3 other) const
{
if (one == other.one)
{
if (tow == other.tow)return three > other.three;
return tow < other.tow;
}
return one < other.one;
}
T3() { one = tow = three = 0; }
T3(T11 one, T22 tow, T33 three) : one(one), tow(tow), three(three)
{
}
};
template <typename T1, typename T2>
void uMax(T1& x, T2 y)
{
if (x < y)x = y;
}
template <typename T1, typename T2>
void uMin(T1& x, T2 y)
{
if (x > y)x = y;
}
constexpr int N = 2e5 + 10;
vector<int> child[N];
int s[N], e[N], tot;
T3<int, int, int> t[N];
int siz;
inline void dfs(const int curr, const int fa)
{
s[curr] = ++tot;
for (const auto nxt : child[curr])if (nxt != fa)dfs(nxt, curr);
e[curr] = tot;
}
int n;
int ans[N];
int bit[N];
//注意保留子树对根的影响,让子树在左边即可
inline bool cmpA(const T3<int, int, int>& x, const T3<int, int, int> y)
{
if (x.one != y.one)return x.one < y.one;
if (x.tow != y.tow)return x.tow < y.tow;
return s[x.three] > s[y.three];
}
inline void add(int x, const int val)
{
for (; x <= n; x += lowBit(x))bit[x] += val;
}
inline int query(int x)
{
int ans = 0;
for (; x; x -= lowBit(x))ans += bit[x];
return ans;
}
inline int Query(const int l, const int r)
{
return query(r) - query(l - 1);
}
//Ai、Bi、i
T3<int, int, int> tmp[N];
//合并两个有序数组
inline void merge(const int L, const int mid, const int R)
{
int i = L, j = mid + 1;
int cnt = L;
while (i <= mid and j <= R)tmp[cnt++] = t[i].tow < t[j].tow ? t[i++] : t[j++];
while (i <= mid)tmp[cnt++] = t[i++];
while (j <= R)tmp[cnt++] = t[j++];
forn(i, L, R)t[i] = tmp[i];
}
inline void cdq(const int L, const int R)
{
const int mid = L + R >> 1;
if (L == R)return;
cdq(L, mid), cdq(mid + 1, R);
int l = L;
forn(r, mid+1, R)
{
int queryPoint = t[r].three;
for (; l <= mid and t[l].tow <= t[r].tow; l++)add(s[t[l].three], 1);
ans[queryPoint] += Query(s[queryPoint], e[queryPoint]);
}
forn(i, L, l-1)add(s[t[i].three], -1);
//去掉B的影响
merge(L, mid, R);
}
inline void solve()
{
cin >> n;
forn(i, 1, n-1)
{
int u, v;
cin >> u >> v;
child[u].push_back(v);
child[v].push_back(u);
}
dfs(1, 0); //处理dfs序
forn(i, 1, n)
{
auto& [A,B,id] = t[i];
cin >> A >> B, id = i;
}
sort(t + 1, t + n + 1, cmpA); //去掉A的影响
cdq(1, n);
forn(i, 1, n)if (ans[i])cout << ans[i] << endl;
}
signed int main()
{
Spider
//------------------------------------------------------
int test = 1;
// read(test);
// cin >> test;
forn(i, 1, test)solve();
// while (cin >> n, n)solve();
// while (cin >> test)solve();
}
\]
P8575 「DTOI-2」星之河 题解的更多相关文章
- 「POJ 3666」Making the Grade 题解（两种做法）
0前言 感谢yxy童鞋的dp及暴力做法! 1 算法标签 优先队列.dp动态规划+滚动数组优化 2 题目难度 提高/提高+ CF rating:2300 3 题面 「POJ 3666」Making th ...
- NBL小可爱纪念赛「 第一弹 」 游记（部分题解）
比赛链接 洛谷:禁止含有侮辱性质的比赛 . ??? 反正我觉得,gyx挺危险的 不说废话. 首先,比赛经验,前几个小时不打,跟着刷榜. 一看 T1. 发现是道水题,直接切掉了. 然后看到了 T2. 感 ...
- LOJ #2542. 「PKUWC 2018」随机游走(最值反演 + 树上期望dp + FMT)
写在这道题前面 : 网上的一些题解都不讲那个系数是怎么推得真的不良心 TAT (不是每个人都有那么厉害啊 , 我好菜啊) 而且 LOJ 过的代码千篇一律 ... 那个系数根本看不出来是什么啊 TAT ...
- LOJ #2538. 「PKUWC 2018」Slay the Spire (期望dp)
Update on 1.5 学了 zhou888 的写法,真是又短又快. 并且空间是 \(O(n)\) 的,速度十分优秀. 题意 LOJ #2538. 「PKUWC 2018」Slay the Spi ...
- fir.im Weekly - 如何打造 Github 「爆款」开源项目
最近 Android 转用 Swift 的传闻甚嚣尘上,Swift 的 Github 主页上已经有了一次 merge>>「Port to Android」,让我们对 Swift 的想象又多 ...
- 【微信小程序】开发实战 之 「视图层」WXML & WXSS 全解析
在<微信小程序开发实战 之 「配置项」与「逻辑层」>中我们详细阐述了小程序开发的程序和页面各配置项与逻辑层的基础知识.下面我们继续解析小程序开发框架中的「视图层」部分.学习完这两篇文章的基 ...
- 「NOIP2016」天天爱跑步 题解
(声明:图片来源于网络) 「NOIP2016」天天爱跑步 题解 题目TP门 题目 题目描述 小c同学认为跑步非常有趣,于是决定制作一款叫做<天天爱跑步>的游戏.<天天爱跑步>是 ...
- 前端构建工具之gulp（一）「图片压缩」
前端构建工具之gulp(一)「图片压缩」 已经很久没有写过博客了,现下终于事情少了,开始写博吧 今天网站要做一些优化:图片压缩,资源合并等 以前一直使用百度的FIS工具,但是FIS还没有提供图片压缩的 ...
- 更新日志 - fir.im「高级统计」功能上线
距离 2016 年到来只剩 10 个日夜,fir.im 也准备了一些新鲜的东西,比如「高级统计」功能和「跳转应用商店」功能,帮助你更好地管理.优化应用,欢迎大家试用反馈:) 新增高级统计功能 这次更新 ...
- Notepad++ 开启「切分窗口」同时检视、比对两份文件
Notepad++ 是个相当好用的免费纯文本编辑器,除了内建的功能相当多之外,也支持外挂模块的方式扩充各方面的应用.以前我都用 UltraEdit 跟 Emeditor,后来都改用免费的 Notepa ...
随机推荐
- S3C2440移植uboot之支持NANDFLASH操作
上一节我们移植了uboot,S3C2440移植uboot之支持NORFLASH.这节我们继续移植,支持NANDFLASH. 目录 编译报错 拷贝s3c2410_nand.c,修改宏定义支持SC32 ...
- P4837
日了啊,这道题每个输入中有多组输入,每处理完一组输入需要清空STL的stack类对象的啊.要是自己写的栈或许能想起来重新top=1,但是这用的STL现成的stack,就忘了while(!sk.empt ...
- Spring boot 运行服务jar外配置配置文件方式总结
本文为博主原创,转载请注明出处: 由于需要在本地编译打包,在服务器上验证某些功能,需要频繁修改配置,本地打包时,会将配置文件也打包的jar 包内部,这种方式下,若修改配置则需要本地修改重新上传服务器一 ...
- ElasticSearch使用实践(文档操作)
可以使用Docker安装ES和Kibana: 使用docker-compose安装ElasticSearch和Kibana: version: '3.1' services: elasticsearc ...
- 【TouchGFX】代码结构
生成代码与用户代码 代码结构图示如下 据上图显示代码结构分为三层 引擎 这是TouchGFX提供的标准类,作为生成类的基类 生成 这是touchgfx designer生成的类,作为用户类的基类,这部 ...
- [转帖]2024年正常使用windows XP之一：系统下载篇
https://zhuanlan.zhihu.com/p/347764175 半夏:2024年正常使用windows XP之一:系统下载篇 半夏:2024年正常使用windows XP之二:补丁及运行 ...
- [转帖]Oracle-UNDO篇
原文地址:https://www.modb.pro/db/70802?xzs= 一:请描述什么是Oracle Undo. 二:请描述UNDO的作用. 三:请谈谈你对Manual Undo Mana ...
- [转帖]mysql - 使用文件中的 mysql 加载数据格式化 csv 日期列
https://www.coder.work/article/2481907#:~:text=LOAD%20DATA%20INFILE%20%27%2Finvoices%2Finvoice138130 ...
- [转帖]tidb集群部署
http://blog.itpub.net/29785807/viewspace-2789852/ 一.安装规划 1 2 3 4 5 6 使用15台服务器 5台tidb服务器:每台3个tidb实例+1 ...
- Jmeter学习之四_kingbaseV8R6数据库的简单验证
Jmeter学习之四_kingbaseV8R6数据库的简单验证 背景 周一没去报道, 因为我忘记体检了... 继续在家进行学习提高自己. jmeter周末时开始看的. 今天想着继续研究一下对数据库的处 ...