动态规划（四）——区间dp

区间dp：

就是对于区间的一种动态规划，对于某个区间，它的合并方式可能有很多种，我们需要去枚举所有的方式，通常是去枚举区间的分割点，找到最优的方式(一般是找最少消耗)。

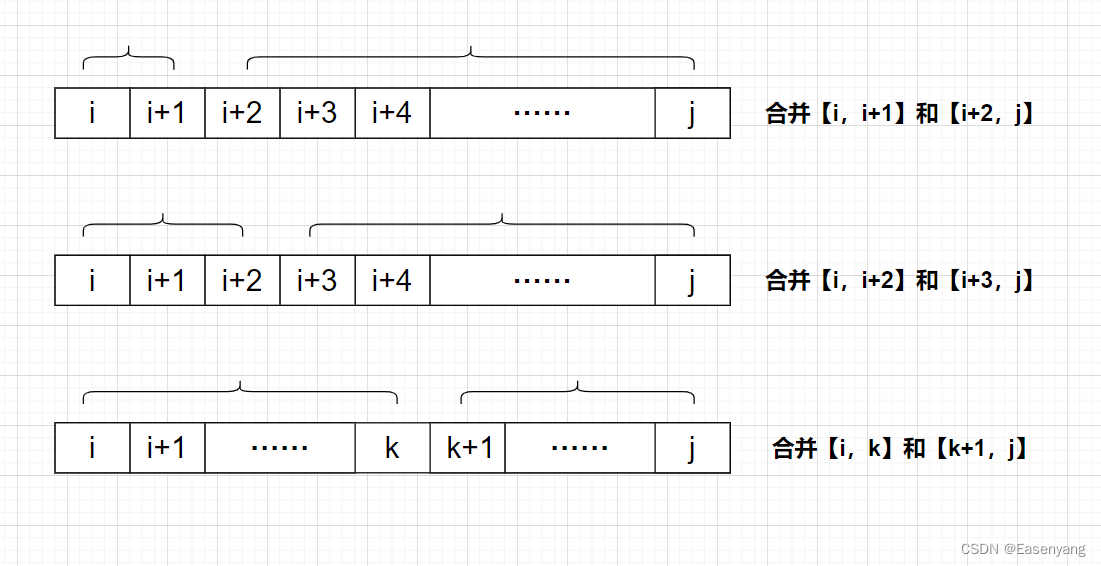
通常都是先枚举区间长度，区间长度为1就不用合并，所以从2开始枚举，然后枚举左端点，那么右端点就为左端点加区间长度-1，再枚举分割点 k，最后计算不同分割点 k 的情况下，合并区间的消耗，dp[i][j]选择其中的最小消耗。（需要注意的是要记得根据题意给上初值）

for (int len = 2; len <= n; len++) {//先枚举区间长度
	for (int i = 1; i+len-1 <= n; i++) {//再枚举区间左端点，左端点加区间长度为右端点，不能大于n
		int j = i+len-1;	//区间右端点
		for (int k = i; k < j; k++) {	//枚举区间分割点
			dp[i][j] = Math.min(dp[i][j], dp[i][k]+dp[k+1][j]+合并区间的消耗);
		}
	}
}

模板题目：石子合并

<简单版>

有N堆石子排成一排(n<=100),现要将石子有次序地合并成一堆，规定每次只能选相邻的两堆合并成一堆，
并将新的一堆的石子数，记为改次合并的得分，编一程序，由文件读入堆数n及每堆石子数(<=200)；

（1）选择一种合并石子的方案，使得做n-1次合并，得分的总和最少
（2）选择一种合并石子的方案，使得做n-1次合并，得分的总和最多

输入格式
第一行为石子堆数n 第二行为每堆石子数，每两个数之间用一空格分隔。

输出格式
从第1行为得分最小第二行是得分最大。

样例
样例输入
4
4 5 9 4
样例输出
44
54

思路：

若最初的第i堆石子和第j堆石子被合并成一堆，则说明i~j之间的每堆石子也已经被合并，这样i和j才有可能相邻。因此，在任意时刻，任意一堆石子均可以用一个闭区间[i,j]来描述，表示这堆石子是由最初的第i~j堆石子合并而成的。另外，一定存在一个整数k(l<=k<r)，在这堆石子形成之前，先有第i~k堆石子(闭区间[l,k])被合并成一堆，第k+1~r堆石子(闭区间[k+1,r])被合并成一堆，然后这两堆石子才合并成[i,j]。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <queue>
#include <vector>
#include <cstdlib>
#include <string>
#include <cstring>
#include <utility>
#define N 1010
using namespace std;
int f[N][N],g[N][N],a[N],s[N],n;
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
		s[i]=s[i-1]+a[i];
	}
	memset(f,0x3f,sizeof(f));
	for(int i=1;i<=n;i++) f[i][i]=0;
	for(int len=2;len<=n;len++){
		for(int i=1;i<=n-len+1;i++){
			int j=i+len-1;
			for(int k=i;k<j;k++){
				f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]+s[j]-s[i-1]);
			    g[i][j]=max(g[i][j],g[i][k]+g[k+1][j]+s[j]-s[i-1]);
			}
		}
	}
	printf("%d\n",f[1][n]);
	printf("%d\n",g[1][n]);
	return 0;
}

例:能量项链

在Mars星球上，每个Mars人都随身佩带着一串能量项链。在项链上有N颗能量珠。
能量珠是一颗有头标记与尾标记的珠子，这些标记对应着某个正整数。
并且，对于相邻的两颗珠子，前一颗珠子的尾标记一定等于后一颗珠子的头标记。
因为只有这样，通过吸盘（吸盘是Mars人吸收能量的一种器官）的作用，这两颗珠子才能聚合成一颗珠子，
同时释放出可以被吸盘吸收的能量。如果前一颗能量珠的头标记为m，尾标记为r，后一颗能量珠的头标记为r，
尾标记为n，则聚合后释放的能量为m*r*n（Mars单位），新产生的珠子的头标记为m，尾标记为n。
需要时，Mars人就用吸盘夹住相邻的两颗珠子，通过聚合得到能量，直到项链上只剩下一颗珠子为止。
显然，不同的聚合顺序得到的总能量是不同的，请你设计一个聚合顺序，使一串项链释放出的总能量最大。 
例如：设N=4，4颗珠子的头标记与尾标记依次为(2，3) (3，5) (5，10) (10，2)。我们用记号⊕表示两颗珠子的聚合操作，
(j⊕k)表示第j，k两颗珠子聚合后所释放的能量。则第4、1两颗珠子聚合后释放的能量为： 
     (4⊕1)=10*2*3=60。 
这一串项链可以得到最优值的一个聚合顺序所释放的总能量为 
     ((4⊕1)⊕2)⊕3）=10*2*3+10*3*5+10*5*10=710。

输入

输入的第一行是一个正整数N（4≤N≤100），表示项链上珠子的个数。第二行是N个用空格隔开的正整数，所有的数均不超过1000。
第i个数为第i颗珠子的头标记（1≤i≤N），当i<n时，第i颗珠子的尾标记应该等于第i+1颗珠子的头标记。第n颗珠子的尾标记应该等于第1颗珠子的头标记。
至于珠子的顺序，你可以这样确定：将项链放到桌面上，不要出现交叉，随意指定第一颗珠子，然后按顺时针方向确定其他珠子的顺序。

输出

输出只有一行，是一个正整数E（E≤2.1*109），为一个最优聚合顺序所释放的总能量。

输入样例

4
2  3  5  10

输出样例

710

诸如此类不能线性规划的问题要用到区间DP，区间DP一般就是三层循环，第一层表示区间长度，第二层枚举起点并根据第一层区间长度算出区间终点，第三层便在当前区间内枚举决策（即哪两个合并）

本题由于是环，还需破环为列，可以开两倍大的数组，即a[i]=a[i+n]，便可在第n颗珠子时求到第1颗珠子的头标记（也即第n颗珠子的尾标记）

合并珠子即合并左珠dp[i][k]和右珠dp[k+1][j]，释放能量a[i]∗a[k+1]∗a[j+1]（注意a[i]存放的是第i颗珠子的头标记，所以a[k+1]才是第k个珠子的尾标记）

代码：

#include <bits/stdc++.h>
#define N 200
using namespace std;
int n,f[N][N],a[N];
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
		a[n+i]=a[i];
	}
	memset(f,0,sizeof(f));
	for(int len=1;len<=n;len++){
		for(int i=1;i<=2*n-len+1;i++){
			int j=i+len-1;
			if(i==j) f[i][j]=0;
			for(int k=i;k<j;k++){
				f[i][j]=max(f[i][j],f[i][k]+f[k+1][j]+a[i]*a[j+1]*a[k+1]);
			}
		}
	}
	int ans=0;
	for(int i=1;i<=n;i++)
		ans=max(ans,f[i][i+n-1]);
	printf("%d\n",ans);
	return 0;
}

如有错误，欢迎各位大佬在评论区指正小蒟蒻博主的错误~

#一名爱打篮球的oier#