【Reverse】初遇花指令

解密花指令

全文参考了一个大师傅的blog：https://blog.csdn.net/zhangmiaoping23/article/details/38400393

介绍

花指令是对抗反汇编的有效手段之一，正常代码添加了花指令之后，可以破坏静态反汇编的过程，使反汇编的结果出现错误。错误的反汇编结果会造成破解者的分析工作大量增加，进而使之不能理解程序的结构和算法，也就很难破解程序，从而达到病毒或软件保护的目的。

实例分析

#include <iostream>
int main()
{
    __asm
    {
        xor eax,eax
        test eax,eax
        je Label1
        _emit 0e8h
        Label1:
    }

    std::cout << "Test Junk Code" << std::endl;
    system("pause");
}

• 将上面的代码编译，然后拖入ida进行分析
  
  
  
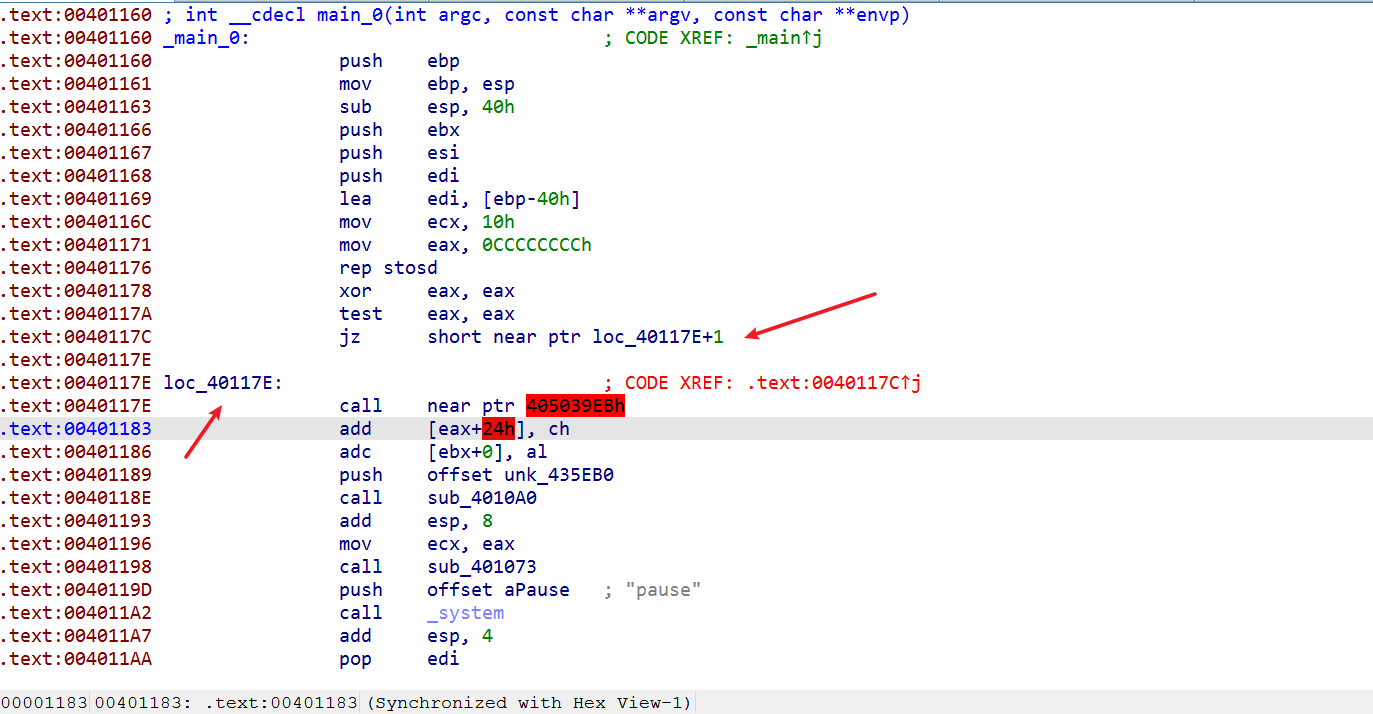
  你会发现这个跳转的数据有些奇怪，和代码段的地址差别有点大，而且无法进行反汇编

• 查看OD分析
  
  

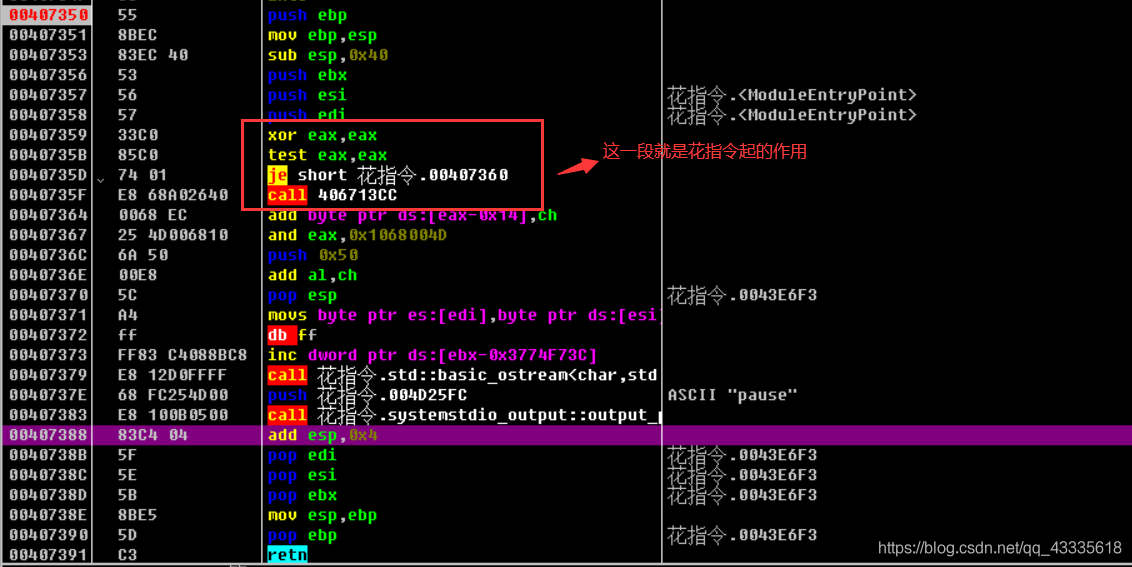
也就是说实际程序运转时，会直接跳到0x00407360处，但由于IDA是静态分析。在反汇编时，是通过指令符识别并进行反汇编的，所以在碰到E8时，会把后面当作操作数，以至于最后反汇编有误。

这也说明了静态分析的缺点

花指令的类型

• 可执行式花指令
  
  顾名思义，可执行式花指令指的是能够正常运行的但又不改变原始程序逻辑性的一组无用指令。这类花指令有如下特点：①可以正常运行；②不改变任何寄存器的值；③反汇编器可以正确反汇编该指令。
  
  例如这样几组花指令就属于该类别：PUSHEAX＆POPEAX；NOP：INCEAX&DECEAX等等。这种类别的花指令组合形式很多，常常用在病毒代码的变形引擎中，病毒在传播时通过变形引擎随机产生一组该类别花指令并插入到病毒正常代码中，可以改变病毒的特征码，从而起到变形的作用。

• 不可执行式花指令(垃圾指令)
  
  本文主要就是讲这个方面，是指被插入到原始代码中但又不改变原始程序逻辑性的一组无用字节。这类花指令有如下特点：①不可以正常运行；②不改变任何寄存器的值；③反汇编器可能会错误反汇编这些字节。
  
  根据反汇编的工作原理，只有当花指令同正常指令的开始几个字节被反汇编器识别成一条指令时，才能有效破坏反汇编的结果。因此，插入的花指令应当是一些不完整的指令，被插入的不完整指令可以是随机选择的。正因为不可执行花指令有这些特点，该类花指令才能应用到软件保护中。
  
  Cullen等人指出为了能够有效“迷惑"静态反汇编工具，同时保证代码的正确运行，花指令必须满足两个基本特征，即：
  
  1)垃圾数据必须是某个合法指令的一部分：
  
  2)程序运行时，花指令必须位于实际不可执行的代码路径。

可执行和不可执行是相对于插入的花指令而言，而非整个程序是可执行或不可执行

不可执行花指令的成功来自反汇编算法的缺陷

当前静态分析中采用的反汇编算法主要可以分为2类：线性扫描算法与行进递归算法。

[3.1]线性扫描反汇编算法

线性扫描算法就是直接将所有的二进制，从头开始进行反汇编，而不作任何判段

[3.2]行进递归反拒绾算法

相比线性扫描算法，行进递归算法通过程序的控制流来确定反汇编的下一条指令，遇到非控制转移指令时顺序进行反汇编，而遇到控制转移指令时则从转移地址处开始进行反汇编。行进递归算法的缺点在于准确确定间接转移目的地址的难度较大。

Thinking

花指令本就属于代码混淆技术的一种，所以它的核心无非就是在保证程序正常运行的情况下，对指令进行修改。例如最简单的无效指令，上面的利用线性扫描反汇编技术的老实，来造成反编译失败的。还有比较花的就是jz,jnz到同一地址，什么蕴含式，设计、利用代码执行的某种必然结果，完成混淆视听的目的。但混淆始终只是疲敌之术。