IoC容器-Bean管理XML方式（p名称空间注入）
5，p名称空间注入（简化xml配置）
（1）使用p名称空间注入，可以简化基于xml配置方式 （了解实际用不多）
第一步 添加 p 名称空间在配置文件中
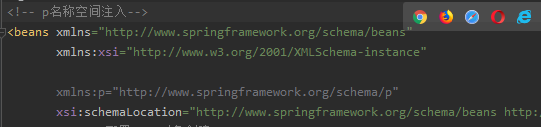
第二步 进行属性注入，在bean标签里面进行操作
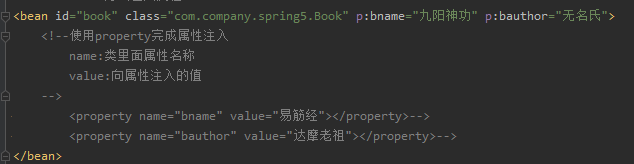
IoC容器-Bean管理XML方式（p名称空间注入）的更多相关文章
- IoC容器-Bean管理XML方式（自动装配）
IoC操作Bean管理(XML自动装配) 1,什么是自动装配 (1)根据指定装配规则(属性名称或者属性类型),Spring自动将匹配的属性值进行注入 2,演示自动装配过程 (1)根据属性名称自动注入 ...
- IoC容器-Bean管理XML方式（创建对象和set注入属性，有参构造注入属性）
Ioc操作Bean管理 1,什么是Bean管理 (0)Bean管理指的是两个操作 (1)Spring创建对象 (2)Spring注入属性 2,Bean管理操作有两种方式 (1)基于xml配置文件方式实 ...
- IoC容器-Bean管理XML方式（引入外部属性文件）
IoC操作Bean管理(引入外部属性文件) 1,直接配置数据库信息 (1)配置德鲁伊连接池 (2)引入德鲁伊连接池依赖jar包 2,通过引入外部属性文件配置数据库连接池 (1)创建外部属性文件,pro ...
- IoC容器-Bean管理XML方式（注入空值和特殊符号）
Ioc操作Bean管理(xml注入其他类型属性), 字面量 (1)null值 (2)属性值包含特殊符号
- IoC容器-Bean管理XML方式（注入集合类型属性）
Ico操作Bean管理(xml注入集合属性) 1,注入数组类型属性 2,注入List集合类型属性 3,注入Map集合类型属性 (1)创建类,定义数组.list.map.set类型属性,生成对应set方 ...
- IoC容器-Bean管理XML方式（注入内部bean和级联赋值）
注入属性-内部bean和级联赋值 (1)一对多关系:部分和员工 一个部门有多个员工,一个员工属于一个部门 部门是一,员工是多 (2)在实体类之间表示一对多关系 (3)在spring配置文件中进行配置 ...
- IoC容器-Bean管理XML方式（注入外部bean）
注入属性-外部bean (1)创建两个类service类和dao类 (2)在service调用dao里面的方法 (3)在spring配置文件中进行配置
- IoC容器-Bean管理注解方式（创建对象）
IoC操作Bean管理(基于注解方式) 1,什么是注解 (1)注解是代码特殊标记,格式:@注解名称(属性名称=属性值,属性名称=属性值...) (2)使用注解,注解作用在类上面,方法上面,属性上面 ( ...
- IoC容器-Bean管理注解方式（注入属性@Autowired和Qualifier）
基于注解方式实现属性注入 (1)@Autowired:根据属性类型进行自动装配 第一步 把 service 和 dao 对象创建,在service 和 dao 类添加创建对象注解 第二步 在servi ...
随机推荐
- JAVA中json对象转JAVA对象，JSON数组（JSONArray）转集合（List）
json格式 {userId:'1',message:'2',create_time:'2020-03-28 20:58:11',create_date:'2020-03-28'}JAVA对象 Cha ...
- 【LeetCode】871. Minimum Number of Refueling Stops 解题报告（Python）
作者: 负雪明烛 id: fuxuemingzhu 个人博客: http://fuxuemingzhu.cn/ 目录 题目描述 题目大意 解题方法 贪心算法 日期 题目地址:https://leetc ...
- 【LeetCode】812. Largest Triangle Area 解题报告（Python）
作者: 负雪明烛 id: fuxuemingzhu 个人博客: http://fuxuemingzhu.cn/ 目录 题目描述 题目大意 解题方法 三重循环 组合函数 日期 题目地址:https:// ...
- 【剑指Offer】序列化二叉树 解题报告（Python）
[剑指Offer]序列化二叉树 解题报告(Python) 标签(空格分隔): 剑指Offer 题目地址:https://www.nowcoder.com/ta/coding-interviews 题目 ...
- JavaScript8种数据类型
一.开门见山 在ES5的时候,我们认知的数据类型确实是 6种:Number.String.Boolean.undefined.object.Null. ES6 中新增了一种 Symbol .这种类型的 ...
- CS5213设计HDMI转VGA带音频方案+设计电路|直接替代AG6200 AG6201
台湾安格AG6200 AG6201专门用于设计HDMI转VGA带音频输出的方案芯片,CS5213是一款HDMI to VGA转换器且结合了HDMI输入接口和模拟RGB DAC输出.带支持片上音频数模转 ...
- Linux磁盘分区与挂载
原理介绍 在Linux世界中,一切皆目录,每一块硬盘分区对应Linux的一个目录,所以我们可以通过管理目录来管理硬盘分区,而将硬盘分区与文件目录关联的操作就成为"挂载"[mount ...
- Java的发展简史
Java是由Sun Microsystems公司(简称Sun公司)于1995 年 5 月推出的 Java程序设计语言和Java平台的总称.Java语言是一种可以撰写跨平台应用软件的面向对象的程序设计语 ...
- css中cursor(光标类型)
值 描述 url 需使用的自定义光标的 URL. 注释:请在此列表的末端始终定义一种普通的光标,以防没有由 URL 定义的可用光标. default 默认光标(通常是一个箭头) auto 默认.浏览器 ...
- 抛砖系列之-MySQL中的数据类型JSON
今天介绍一个MySQL中的数据类型-JSON,相信大家对JSON都不陌生,在日常工作中使用到的频率也很高,话不多说,直接开始. 何谓JSON 看下RFC文档对于JSON的描述 1.基于 JavaScr ...