YbtOJ#832-鸽子饲养【凸包,Floyd】

正题

题目链接:https://www.ybtoj.com.cn/contest/116/problem/3

---

题目大意

给出两个大小分别为\(n,m\)的点集\(A,B\)。

求出\(B\)的一个最小子集使得该子集的凸包包含了所有点集\(A\)中的点。

无解输出\(-1\)

\(2\leq n\leq 10^5,3\leq m\leq 500\)

---

解题思路

选出的子集肯定是一个凸包，凸包就是相邻点连边之间的半平面交。

所以可以理解为我们要找到一些点对使得它们的半平面包含点集\(A\)。

如果\(x->y\)的半平面（左右都一样，反过来就是了）包含点集\(A\)，那么\(x\)向\(y\)连边，那么问题就变为了求图的最小环。这个可以\(Floyd\)解决。

如何判断一个半平面是否包含点集\(A\)？

一个类似旋转卡壳的想法是对于给出的这个半平面的斜率，我们在点集\(A\)的凸包上找到两个节点卡住它。（如下图）



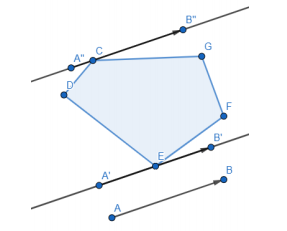
然后判断这两个点是否在半平面内就好了。

挺麻烦的，再简化一下，我们将\(A\)的凸包用\(x\)坐标最大/小的两个节点分成两半，那么凸包就变成了一个上凸壳和一个下凸壳。

然后我们要找到的两个点，这个两个点肯定是一个在上一个在下的，我们根据半平面的斜率在上下凸壳上面二分一下就好了。

时间复杂度\(O(n+m^2\log n+m^3)\)

---

code

#include<cstdio>
#include<cstring>
#include<algorithm>
#define ll long long
using namespace std;
const ll N=1e5+10,M=510;
struct point{
	ll x,y;
	point(ll xx=0,ll yy=0)
	{x=xx;y=yy;return;}
}g[N],u[N],v[N],s[N],p[M];
ll n,m,uc,vc,f[M][M],h[M][M],ans;
point operator+(point a,point b)
{return point(a.x+b.x,a.y+b.y);}
point operator-(point a,point b)
{return point(a.x-b.x,a.y-b.y);}
ll operator*(point a,point b)
{return a.x*b.y-a.y*b.x;}
ll solve(point *a,ll n,ll op){
	ll top;s[top=1]=a[1];
	for(ll i=2;i<=n;i++){
		while(top>1&&(s[top]-s[top-1])*(a[i]-s[top-1])*op>=0)top--;
		s[++top]=a[i];
	}
	for(ll i=1;i<=top;i++)
		a[i]=s[i];
	return top;
}
bool check(point a,point b){
	ll op=1;
	if(a.x>b.x)swap(a,b),op=-1;
	ll l=1,r=uc-1;
	while(l<=r){
		ll x=(l+r)>>1;
		if((b-a)*(u[x+1]-u[x])>=0)l=x+1;
		else r=x-1;
	}
	if((b-a)*(u[l]-a)*op<0)return 0;
	l=1,r=vc-1;
	while(l<=r){
		ll x=(l+r)>>1;
		if((b-a)*(v[x+1]-v[x])<=0)l=x+1;
		else r=x-1;
	}
	if((b-a)*(v[l]-a)*op<0)return 0;
	return 1;
}
bool cmp(point a,point b)
{return a.x<b.x;}
signed main()
{
	freopen("lo.in","r",stdin);
	freopen("lo.out","w",stdout);
	scanf("%lld%lld",&n,&m);
	ll L=1,R=1;
	for(ll i=1;i<=n;i++)
		scanf("%lld%lld",&g[i].x,&g[i].y);
	sort(g+1,g+1+n,cmp);
	for(ll i=1;i<=n;i++){
		ll w=(g[n]-g[1])*(g[i]-g[1]);
		if(w>=0)u[++uc]=g[i];
		if(w<=0)v[++vc]=g[i];
	}
	uc=solve(u,uc,1);
	vc=solve(v,vc,-1);
	for(ll i=1;i<=m;i++)
		scanf("%lld%lld",&p[i].x,&p[i].y);
	for(ll i=1;i<=m;i++)
		for(ll j=1;j<=m;j++){
			if(i==j){h[i][j]=f[i][j]=1e9;continue;}
			h[j][i]=f[i][j]=check(p[i],p[j])?1:1e9;
		}
	for(ll k=1;k<=m;k++)
		for(ll i=1;i<=m;i++)
			for(ll j=1;j<=m;j++)
				f[i][j]=min(f[i][j],f[i][k]+f[k][j]);
	ans=1e9;
	for(ll i=1;i<=m;i++)
		for(ll j=1;j<=m;j++)
			ans=min(ans,f[i][j]+h[i][j]);
	if(ans>=1e9)puts("-1");
	else printf("%lld\n",ans);
	return 0;
}