Gym 100169E Tetrahedron Inequality

大致题意：

给出六条边，判断是否能组成四面体

分析：

四面体由四个三角形组成，所以每一条边肯定要符合三角形的任意两边大于第三边的性质。一开始以为这样判断就可以了，然而这题并没有这么简单。

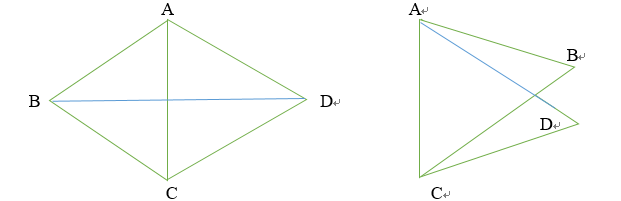
如右图，有四个三角形，六条边，但是并不是四面体

如下图，先选择五条边(绿色的五条边)，然后展开成一个平面，三角形ABC和三角形ACD不重叠(重叠)，此时只要将三角形ABC绕着AC轴旋转，BD即第六条边。所以展开成平面可求除最大值(最小值)

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <string>
#include <map>
#include <cmath>
using namespace std;

const int maxn=10000+5;
int a[6];
int edge[6];
bool flag[6];

bool isTriangle(int x,int y,int z)
{
    return x+y>z && x+z>y && y+z>x;
}
bool isTetrahedron()
{
    double BD=edge[0]/1000.0;
    double AB=edge[1]/1000.0;
    double AD=edge[2]/1000.0;
    double CD=edge[3]/1000.0;
    double BC=edge[4]/1000.0;
    double AC=edge[5]/1000.0;

    //方法一：角度数求出来
    double ABD=acos((AB*AB+BD*BD-AD*AD)/(2*AB*BD));
    double CBD=acos((BC*BC+BD*BD-CD*CD)/(2*BC*BD));
    double minAC=sqrt(AB*AB+BC*BC-2*AB*BC*cos(ABD+CBD));
    double maxAC=sqrt(AB*AB+BC*BC-2*AB*BC*cos(ABD-CBD));
    if(minAC>maxAC) swap(minAC,maxAC);

    //方法二：
    /*double cosABD=(AB*AB+BD*BD-AD*AD)/(2*AB*BD);
    double cosCBD=(BC*BC+BD*BD-CD*CD)/(2*BC*BD);
    double sinABD=sqrt(1-cosABD*cosABD);
    double sinCBD=sqrt(1-cosCBD*cosCBD);
    double cosABC=cosABD*cosCBD-sinABD*sinCBD;
    double maxAC=sqrt(AB*AB+BC*BC-2*AB*BC*cosABC);
    cosABC=cosABD*cosCBD+sinABD*sinCBD;
    double minAC=sqrt(AB*AB+BC*BC-2*AB*BC*cosABC);*/

    return AC>minAC && AC<maxAC;
}
bool dfs(int cnt)
{
    if(cnt==3)
        if(!isTriangle(edge[0],edge[1],edge[2])) return false;
    if(cnt==6)
        return isTriangle(edge[0],edge[3],edge[4]) &&
               isTriangle(edge[1],edge[4],edge[5]) &&
               isTriangle(edge[2],edge[4],edge[5]) &&
               isTetrahedron();
    for(int i=0; i<6; i++)
        if(!flag[i])
        {
            flag[i]=1;
            edge[cnt]=a[i];
            if(dfs(cnt+1)) return true;
            flag[i]=0;
        }
    return false;
}
int main()
{
    //freopen("in.txt","r",stdin);
    int n;
    scanf("%d",&n);
    while(n--)
    {
        for(int i=0; i<6; i++)
            scanf("%d",&a[i]);
        memset(flag,0,sizeof(flag));
        printf("%s\n",dfs(0)? "YES":"NO");
    }
    return 0;
}