Chapter 7 Confounding

目录

• 7.1 The structure of confounding
• Confounding and exchangeability
• Confounding and the backdoor criterion
• 7.4 Confounding and confounders
• 7.5 Single-world intervention graphs
• Confounding adjustment
• Fine Point
  • The strength and direction of confounding bias
  • Identification of conditional and unconditional effects
  • Surrogate confounders
  • Confounders cannot be descendants, but can be in the future of treatment
• Technical Point
  • Does conditional exchangeability imply the backdoor criterion?
  • Fixing the traditional definition of confounder
  • Difference-in-differences and negative outcome controls
  • The front door criterion

Hern\(\'{a}\)n M. and Robins J. Causal Inference: What If.

这一节介绍了一个confounding的概念, 在观测数据中, confounder往往是让人头疼的存在.

backdoor path: 指的是intervention\(A\)和outcome\(Y\)间的一条路径(没有方向要求), 其中存在一个箭头指向\(A\), 但是没有从\(A\)出发的箭头.

注: 存疑

7.1 The structure of confounding

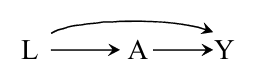
如上图所示, 倘若没有\(L\)的存在, 计算causal effect, 可以直接通过

\[\mathrm{Pr} [Y|A=1] - \mathrm{Pr} [Y|A=0],
\]

来计算, 但是\(L\)的存在导致可交换性不成立, 当然在这个情况下, 我们可以通过standardization, 或者 IP weighting来计算(因为条件可交换性是存在的).

\(L\)是intervention \(A\) 和 预测 \(Y\)的共同的一个cause, 是干扰我们判断的存在, 所以称之为confounder, 这种由\(L\)带来额外的association的现象称之为confounding.

Confounding and exchangeability

这里引入了backdoor criterion的概念, 就是用于判断可交换性是否成立的一个准则.

Confounding and the backdoor criterion

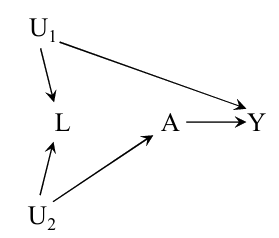
一个非常特殊的情况是, 上图中的\(A \amalg Y\), 但是 \(A \not{\amalg} Y | L\).

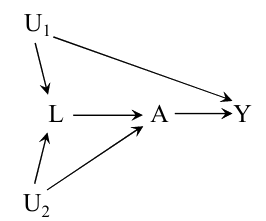
再看上图, 在这种情况下, 无论是否在给定\(L\)的条件下, \(A\)和\(Y\)都是不独立的, 除非给定\(U_1, U_2\).

7.4 Confounding and confounders

7.5 Single-world intervention graphs

介绍了一个更为细致的表示方式: SWIG.

Confounding adjustment

Fine Point

The strength and direction of confounding bias

Identification of conditional and unconditional effects

Surrogate confounders

Confounders cannot be descendants, but can be in the future of treatment

Technical Point

Does conditional exchangeability imply the backdoor criterion?

Fixing the traditional definition of confounder

Difference-in-differences and negative outcome controls

The front door criterion

\[\mathrm{Pr}[Y^a=1] =
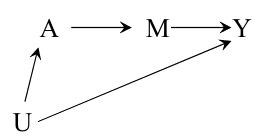
\sum_m
\mathrm{Pr} [M=m|A=a]
\sum_{a'}
\mathrm{Pr} [Y=1|M=m,A=a']
\mathrm{Pr} [A=a'].
\]