Python数学建模系列（一）：规划问题之线性规划

@

目录

• 前言
• 线性规划
  • 样例1：求解下列线性规划问题
    • scipy库求解
  • 样例2：求解下列线性规划问题
    • pulp库求解
  • 样例3.运输问题
• 说明
• 结语

前言

Hello！小伙伴！

非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您指出～

 

自我介绍 ଘ(੭ˊᵕˋ)੭

昵称：海轰

标签：程序猿｜C++选手｜学生

简介：因C语言结识编程，随后转入计算机专业，有幸拿过一些国奖、省奖...已保研。目前正在学习C++/Linux/Python

学习经验：扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语！

 

初学Python 小白阶段

文章仅作为自己的学习笔记 用于知识体系建立以及复习

题不在多 学一题 懂一题

知其然 知其所以然！

 

本文仅从Pyhton如何解决建模问题出发

未对建模思路等进行深一步探索

线性规划

​

线性规划求解需要清晰两部分，目标函数(max, min) 和 约束条件 ，求解前应转化为标准形式：

样例1：求解下列线性规划问题

\[max z = 2x_1 + 3x_2 - 5x_3
\]

\[ s.t. = \begin{cases}
x_1 + x_2 + x_3 = 7 \\
2x_1 - 5x_2 + x_3 >= 10\\
x_1 + 3x_2 + x_3 <= 12\\
x_1,x_2,x_3 >= 0
\end{cases}
\]

scipy库求解

涉及知识点

• optimize.linprog

Demo代码

from scipy import optimize
import numpy as np
c = np.array([2,3,-5])
A = np.array([[-2,5,-1],[1,3,1]])
B = np.array([-10,12])
Aeq = np.array([[1,1,1]])
Beq = np.array([7])
res = optimize.linprog(-c,A,B,Aeq,Beq)
res

运行结果

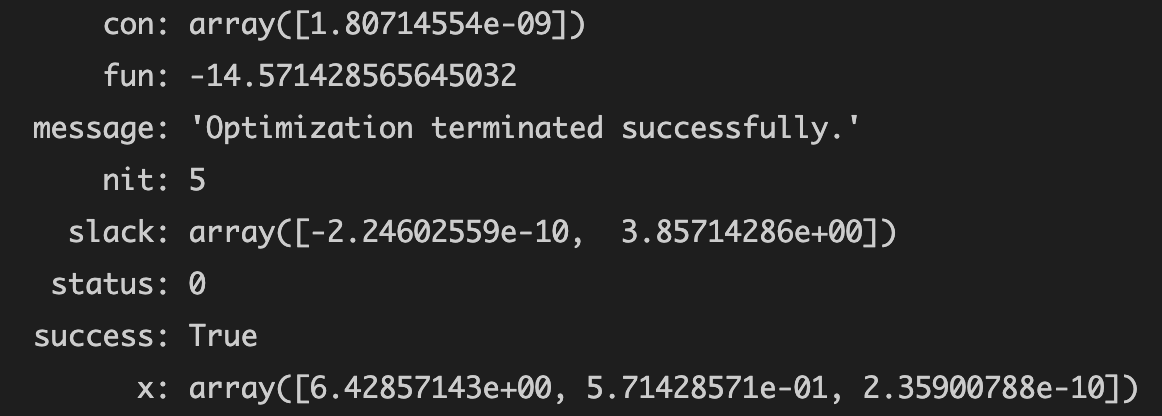
注：x结果为array数组，从左到右依次表示x1 x2 x3....

对很大/小的数不使用科学计数法 np.set_printoptions(suppress=True)

Demo代码

from scipy import optimize
import numpy as np
np.set_printoptions(suppress=True)
c = np.array([2,3,-5])
A = np.array([[-2,5,-1],[1,3,1]])
B = np.array([-10,12])
Aeq = np.array([[1,1,1]])
Beq = np.array([7])
res = optimize.linprog(-c,A,B,Aeq,Beq)
res

运行结果

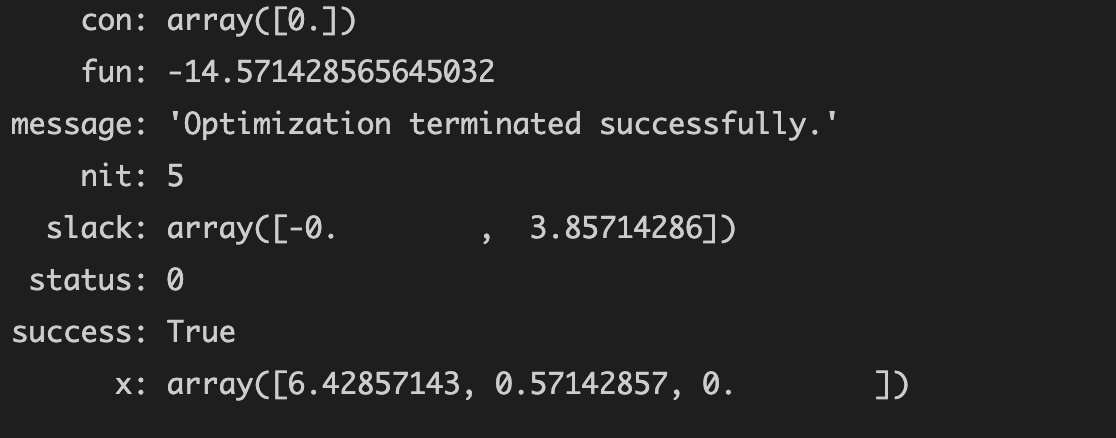
样例2：求解下列线性规划问题

pulp库求解

设计知识点

• LpProblem(name='NoName', sense=LpMinimize)
• solve(solver=None, **kwargs)
• LpVariable(name, lowBound=None, upBound=None, cat='Continuous', e=None)

Demo代码

import pulp as pp

# 目标函数的系数
z = [2, 3, 1]
a = [[1, 4, 2], [3, 2, 0]]
b = [8,6]
aeq = [[1,2,4]]
beq = [101]

# 确定最大最小化问题，当前确定的是最大化问题
m = pp.LpProblem(sense=pp.LpMaximize)

# 定义三个变量放到列表中
x = [pp.LpVariable(f'x{i}', lowBound=0) for i in [1, 2, 3]]

# 定义目标函数，并将目标函数加入求解的问题中
m += pp.lpDot(z, x) # lpDot 用于计算点积

# 设置比较条件
for i in range(len(a)):
    m += (pp.lpDot(a[i], x) >= b[i])

# 设置相等条件
for i in range(len(aeq)):
    m += (pp.lpDot(aeq[i], x) == beq[i])

# 求解
m.solve()
# 输出结果
print(f'优化结果：{pp.value(m.objective)}')
print(f'参数取值：{[pp.value(var) for var in x]}')

运行结果：



注：

• 最优结果为202
• x1 = 101 x2=0 x3=0

样例3.运输问题

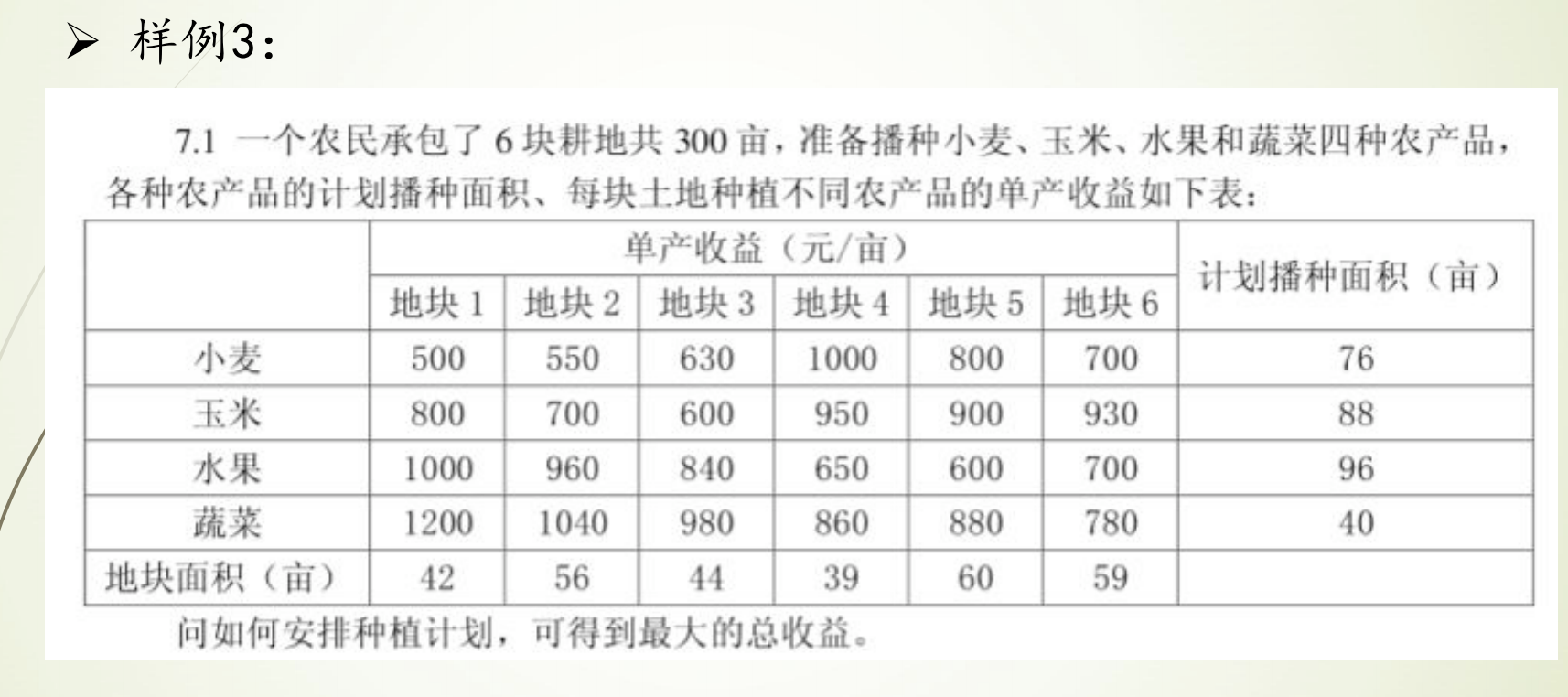
Demo代码

import pulp
import numpy as np
from pprint import pprint

def transportation_problem(costs, x_max, y_max):
    row = len(costs)
    col = len(costs[0])
    prob = pulp.LpProblem('Transportation Proble',sense=pulp.LpMaximize)
    var = [[pulp.LpVariable(f'x{i}{j}',lowBound=0,cat=pulp.LpInteger) for j in range(col)] for i in range(row)]
    # 转为一维
    flatten = lambda x:[y for l in x for y in flatten(l)] if type(x) is list else [x]
    prob += pulp.lpDot(flatten(var),costs.flatten())
    for i in range(row):
        prob += (pulp.lpSum(var[i]) <= x_max[i])
    for j in range(col):
        prob += (pulp.lpSum([var[i][j] for i in range(row)]) <= y_max[j])
    prob.solve()
    return {'objective':pulp.value(prob.objective),'var':[[pulp.value(var[i][j]) for j in range(col)] for i in range(row)]}

costs = np.array([[500,550,630,1000,800,700],
                [800,700,600,950,900,930],
                [1000,960,840,650,600,700],
                [1200,1040,980,860,880,780]])
max_plant = [76,88,96,40]
max_cultivation = [42,56,44,39,60,59]
res = transportation_problem(costs, max_plant, max_cultivation)
print(f'最大值为{res["objective"]}')
print("各个变量的取值为：")
pprint(res['var'])

运行结果：

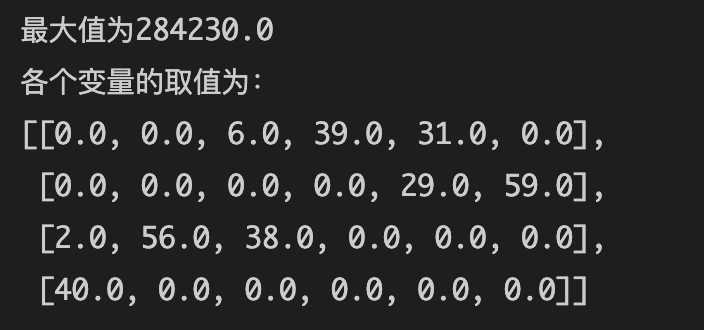
说明

运行环境：Vs Code

结语

学习来源：B站及其课堂PPT，对其中代码进行了复现

链接：https://www.bilibili.com/video/BV12h411d7Dm? from=search&seid=5685064698782810720

文章仅作为学习笔记，记录从0到1的一个过程

希望对您有所帮助，如有错误欢迎小伙伴指正～

我是 海轰ଘ(੭ˊᵕˋ)੭

如果您觉得写得可以的话，请点个赞吧

谢谢支持 ️