亲测可用，可以嵌入word。



【我们为什么要用MathType】

tex不香嘛，但是学校给的模板只有word，word输入公式点起来实在是太麻烦了。



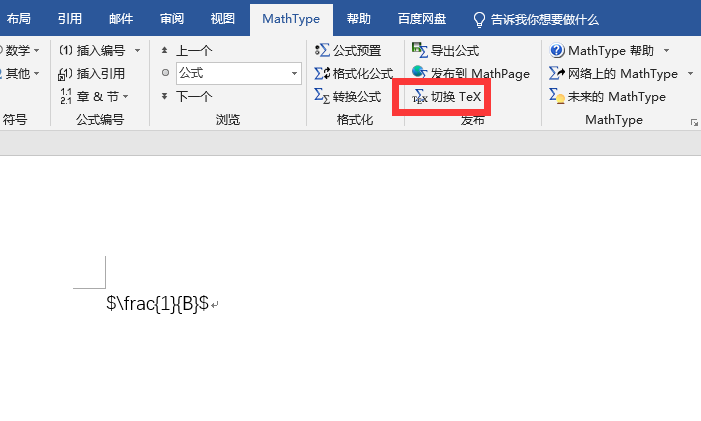
有了这个就可以直接输入公式转换啦。

【安装破解教程】

1.把原来的mathtype卸载干净。

2.解压压缩包，打开文件“MathType-win-zh.exe”，安装新mathtype。

3.安装好后，用刚刚解压的文件夹中的MathType.exe，替换掉安装目录下的MathType.exe。

4.解压Mathtype7.xCrack，用里面的mathtypelib.exe，替换掉安装目录下System文件夹里对应的mathtypelib.exe文件。

5.完成安装。

【链接】

链接：https://pan.baidu.com/s/19kwFQtxT0igKPs0H_6p_aQ

提取码：d5mm

【科研工具】MathType7.2的安装破解与使用的更多相关文章

  1. Xamarin Mono For Android 4.6.07004 完整离线安装破解版（C#开发Android、IOS工具）

      Xamarin是由Miguel de Icaza成立的一家新的独立公司,目的是给Mono一个继续奋斗的机会.Mono for Android (原名:MonoDroid)可以让开发人员使用 Mic ...

  2. LoadRunner 11 安装破解

    安装前的准备: 下载地址: A:安装介质 loadrunner-11.iso:http://yunpan.cn/cHN7JpYPi57wL (提取码:79f0) lm70.dll:http://yun ...

  3. loadrunner11.0 安装破解详解使用教程

    loadrunner11.0 安装破解详解使用教程 来源:互联网 作者:佚名 时间:01-21 10:25:34 [大 中 小] 很多朋友下载了loadrunner11但不是很会使用,这里简单介绍下安 ...

  4. Cadence OrCad Allegro SPB 16.6 下载及安装破解指南

    Cadence公司的电子设计自动化产品涵盖了电子设计的整个流程,包括系统级设计,功能验证,IC综合及布局布线,模拟.混合信号及射频IC设计,全定制集成电路设计,IC物理验证,PCB设计和硬件仿真建模等 ...

  5. ENVI5.1安装破解教程

    原文地址:  ENVI5.1安装破解_百度经验 http://jingyan.baidu.com/article/020278118b5ded1bcd9ce57a.html   ENVI5.1_x86 ...

  6. ERDAS IMAGINE 9.2安装破解方法

    Install the application. Copy the license.dat and ERDAS.exe to C:\Program Files\Leica Geosystems\Sha ...

  7. Adobe Acrobat XI Pro安装破解

    注册机使用说明: Install Instructions: (Read carefully!) 安装说明(仔细阅读!) 1. Disable your Network card or pull th ...

  8. Confluence5.1 最新版的安装&破解&汉化

    转自 博客 http://seanzhou.iteye.com/blog/1287016 亲自基本上按照这个教程装了一遍,成功运行. 1.介绍 Atlassian Confluence(简称Confl ...

  9. Sublime Text 3 Build 3047 32bit/64bit 简体中文安装破解版

    Sublime Text 3 Build 3047 32bit/64bit 简体中文安装破解版 Sublime Text 3 Build 3047 32bit 简体中文安装破解版下载:http://y ...

随机推荐

  1. 『学了就忘』Linux软件包管理 — 44、在RPM包中提取文件

    目录 1.RPM包中文件的提取 2.在RPM包中提取文件的操作 (1)cpio命令介绍 (2)提取RPM包中文件 1.RPM包中文件的提取 为什么要做这个事呢? 在操作Linux系统的时候误删除一个文 ...

  2. Ubuntu軟件商店加載失敗的解決方法

    Ubuntu軟件商店有的时候加载不出来,先用下面的试试 sudo apt install python-apt 如果不行,继续下面的方法 打开终端,运行下面的命令: sudo apt-get upda ...

  3. 调用企业微信API拨打紧急通知电话

    # 前提条件:企业信息:行业类型必须属于"医疗"大类,客服反馈说目前不支持其他行业# 准备工作:https://work.weixin.qq.com/api/doc/90000/9 ...

  4. C#窗体学习

    //进度条控件 private void button1_Click(object sender, EventArgs e)        {            int i;            ...

  5. 分析师机构发布中国低代码平台现状分析报告，华为云AppCube为数字化转型加码

    摘要:Forrester指出,中国企业数字化转型过程中,有58%的决策者正在采用低代码工具进行软件构建,另有16%的决策者计划采用低代码. 华为消息,知名研究与分析机构Forrester Resear ...

  6. Asp.Net Core中简单使用日志组件log4net

    本文将简单介绍在.NET 6中使用log4net的方法,具体见下文范例. 1.首先新建一个ASP.NET Core空项目 2.通过Nuget包管理器安装下面两个包 log4net Microsoft. ...

  7. [bzoj5416]冒泡排序

    结论:一个序列是好序列当且仅当其不存在长度为3的下降子序列 证明:考虑提示,一个长度为3的下降子序列必然会交换三次, 而这三次带来的收益实际上只有2,因此不合法 同时还可以得到:第i个数,要么是前缀最 ...

  8. [atAGC048E]Strange Relation

    考虑对于$\{a_{i+1},...,a_{n}\}$,在其前面插入$a_{i}$对$x_{i}$的影响(不考虑$a_{1}$到$a_{i-1}$): 1.$x_{i}=0$,因为其前面没有数字了 2 ...

  9. 洛谷 P4749 - [CERC2017]Kitchen Knobs（差分转换+dp，思维题）

    题面传送门 一道挺有意思的思维题. 首先有一个 obvious 的结论,就是对于每个炉子,要么转到哪里都符合条件,要么存在唯一的最大值.对于转到哪儿都符合条件的炉子我们 duck 不必考虑它,故我们只 ...

  10. MYSQL5.8----M3

    333333333333333333333333333 mysql> DESC user; +----------+---------------------+------+-----+---- ...