duxing201606的原味鸡树

链接

[http://murphyc.fun/problem/4011]

题意

描述

众所周知，duxing哥非常喜欢原味鸡。众所周知，原味鸡是长在原味鸡树上的。

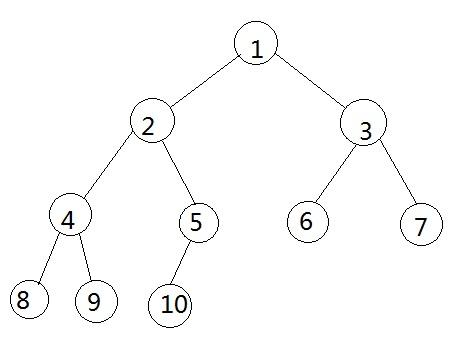
duxing哥因为是水产巨子，所以就购买了一棵原味鸡树。原味鸡树是一颗有n个节点的完全二叉树（节点编号从1开始），每个节点会长出一个原味鸡。每当duxing哥想吃原味鸡的时候，他就会在原味鸡树上挑选一个节点，然后将这个节点的子树上的原味鸡都吃掉（包括选中的那个节点）。

因为duxing哥害怕摘下的鸡不够他吃，所以现在duxing哥想知道当他选择某个节点的时候能吃到多少原味鸡。

输入

第一行n,m，其中n代表这颗树有多少个节点，m代表duxing哥的询问次数(1<=n<=1e9,1<=m<=100000)

接下来m行，每行一个数字x，代表duxing哥询问的节点编号

输出

对于duxing哥的每次询问，输出一个数字代表他能吃到多少原味鸡

输入样例 1

10 4

5

3

6

2

输出样例 1

2

3

1

6

分析

找规律

完全二叉树，k为节点的子树节点个数

从节点序号出发，每次*2，看代码应该懂了

代码

#include<iostream>
#include<stdio.h>
#include<map>
using namespace std;
int n,k;
using namespace std;
int  main(){
	//freopen("in.txt","r",stdin);
	scanf("%d%d",&n,&k);
	while(k--){
		int q;
		scanf("%d",&q);
		int  sum=0,k=1;
		while(1){
			sum+=k;
			q*=2;
			if(q>=n) break;
			k*=2;
		}
		if(q==n)
			cout<<sum+1<<endl;

		else if(q/2+k<n) cout<<sum<<endl;
		else
		{
			sum+=n-q/2+1-k;
			cout<<sum<<endl;
		}
	}
	return 0;
}