Codeforces 982E Billiard 扩展欧几里德

原文链接http://www.cnblogs.com/zhouzhendong/p/9055728.html

题目传送门 - Codeforces 928E

题意

　　一束与坐标轴平行或者成$45^\circ$角的光线在一个矩形区域内反射。

　　如图：

　　

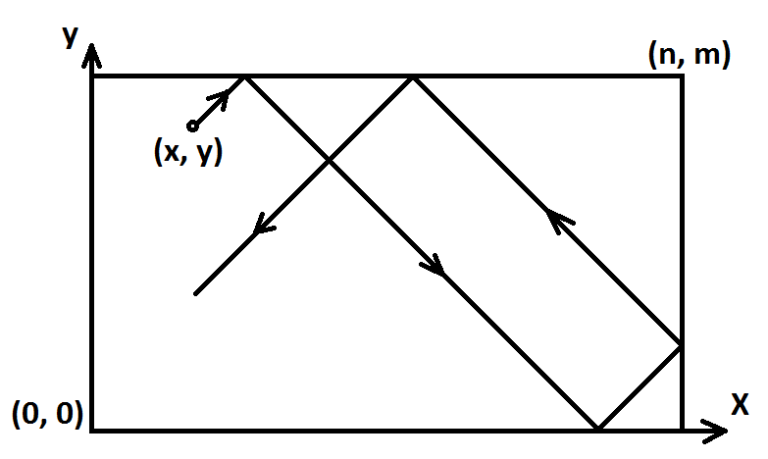
　　给定矩形的长宽，以及光源位置、光线初始方向，问它最先到达四个角落中的哪一个角落。如果永远不能到达，输出$-1$。

题解

　　本来不想写的。本次CF又打烂了。

　　D题一个傻逼错误调了40多分钟。

　　E题貌似挺可做的。可是来不及啊。（再加上深更半夜神志不清）

　　

　　我们来回顾一下初中数学套路。

　　考虑将每次反射做一个对称。

　　我来画一下一组数据：

　　5 3 4 0 1 1

　　

　　通过对称，我们把它画成这样（经典初中数学套路）：

　　

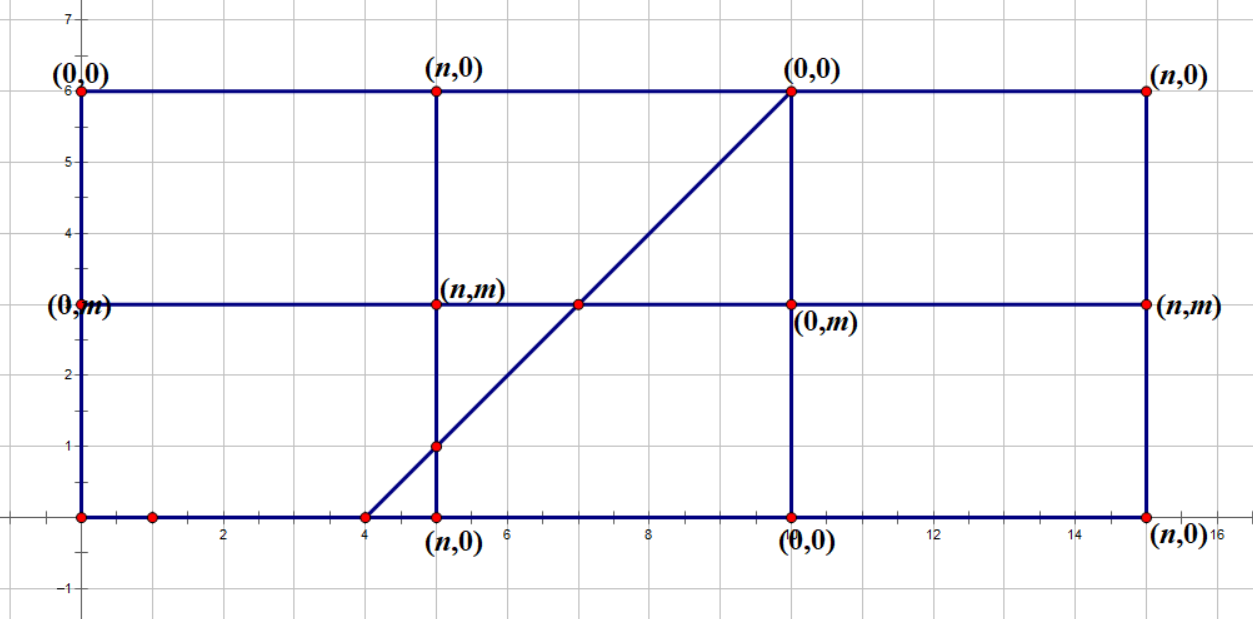
　　然后问题就大致变成了求直线到达的第一个满足$n|T_x,m|T_y$的点$(T_x,T_y)$。

　　为了方便，我们再把原图画成这样：

　　

　　问题进一步简化，变成从$s'$出发的问题了。

　　设$S=(x,y)$，则$S'=(0,y-x)$，

　　不难列出方程：

　　$an+(y-x)=bm \Longrightarrow an+bm=(x-y)$

　　然后我们用exgcd来解一下这个方程，首先判掉无解的情况，输出$-1$。

　　然后注意一下我们要求的是第一个碰到的这样的点，所以在特殊情况的时候要小心。

　　要取$a$的尽量小的正整数值。我一开始写错了，对$m$取模，然后突然发现应该对$m/gcd(n,m)$取模……

　　然后根据算出来的$a$以及$b$的奇偶性来确定到达的位置。

　　至于一开始输入的：

　　　　如果是平行坐标轴的，那么直接判掉。

　　　　如果是$45^\circ$的，那么我们可以通过在原矩形中取对称来使其变成我们需要的那样。

　　题外话：

　　又错失一次上黄的机会QAQ。

　　话说我的代码跑的挺快的。

　　话说为什么目前我$friends$里面的三位大佬（xza，bestfy，emoairx）的代码怎么都要跑几百$MS$……后来才发现他们的那个循环好像不是$O(1)$的……

　　QAQ大佬都会写循环……只有我这种菜鸡才去写公式。关键是还写挂了调了有一会儿……（就是之前提到过的那个问题）

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
int n,m,x,y,vx,vy;
int refx,refy;
LL exgcd(LL a,LL b,LL &x,LL &y){
	if (!b){
		x=1,y=0;
		return a;
	}
	LL res=exgcd(b,a%b,y,x);
	y-=(a/b)*x;
	return res;
}
int main(){
	scanf("%d%d%d%d%d%d",&n,&m,&x,&y,&vx,&vy);
	if (vx==0){
		if (x==0||x==n){
			if (vy==1)
				printf("%d %d\n",x,m);
			else
				printf("%d %d\n",x,0);
		}
		else
			puts("-1");
		return 0;
	}
	if (vy==0){
		if (y==0||y==m){
			if (vx==1)
				printf("%d %d\n",n,y);
			else
				printf("%d %d\n",0,y);
		}
		else
			puts("-1");
		return 0;
	}
	if (vx==-1)
		refx=1,x=n-x;
	if (vy==-1)
		refy=1,y=m-y;
	//s'=(0,y-x)
	//an+(y-x)=bm => an+bm=(x-y)
	LL a,b,g;
	g=exgcd(n,m,a,b);
	if ((x-y)%g!=0){
		puts("-1");
		return 0;
	}
	LL t=(x-y)/g;
	a*=t,b*=t;
	int _m=m/g,_n=n/g;
	LL _a=(a%_m+_m+_m-1)%_m+1,_b=-((x-y)-_a*n)/m;
	LL ansx=n,ansy=m;
	if (_a%2==0)
		ansx=n-ansx;
	if (_b%2==0)
		ansy=m-ansy;
	if (refx)
		ansx=n-ansx;
	if (refy)
		ansy=m-ansy;
	printf("%I64d %I64d",ansx,ansy);
	return 0;
}