POJ 2914 Minimum Cut【最小割 Stoer-Wangner】

题意：求全局最小割

不能用网络流求最小割，枚举举汇点要O(n)，最短增广路最大流算法求最大流是O(n²m)复杂度，在复杂网络中O(m)=O(n²)，算法总复杂度就是O(n⁵)；就算你用其他求最大流的算法，算法总复杂度也要O(n⁴)。所以用网络流算法求解最小割集复杂度不会低于O(n⁴)。所以就要用Stoer_Wagner算法。算法复杂度为O(n³)。如果加堆优化，复杂度会降为O(n²logn)。

Stoer_Wagner算法： 
Stoer_Wagner算法是求无向图全局最小割的一个有效算法，最坏时间复杂度O(n³)，主要思想是先找任意2点的最小割，然后记录下这个最小割，再合并这2个点。这样经过n−1次寻找任意2点最小割，每次更新全局最小割。最后整张图缩成一个点，算法结束，所保存下来的最小割就是全局最小割。

具体步骤：

如果G的最小割Cut把G分成M，N两个点集，那么枚举的s和t无非以下两种情况：

①：如果s∈M，t∈N则Min-C(s，t) = Cut（最终的最小割）

②：如果s，t∈M（或s，t∈N）则Min-C (s，t) >= Cut（合并s和t后并不影响最小割，所以就把st合并了得到中间结果图G'，继续在图G'上求最小割直到命中条件①）

因为利用到了中间结果G'，G'<G，所以降低了复杂度。另外，这个合并的思想有点像Prim最小生成树算法，prim维护的dis数组的含义是集合A外的点到到集合树的最短边权，而Stoer−Wagner维护的w数组是集合A外的点，到集合A所有点的边权之和【割集】。

至于②中提到的合并操作，定义为Contract(s,t) := 删掉点 s, t 及边(s, t)，加入新节点 c，对于任意 v ∈ 与s,t联通的点集，做一条新的边w(v, c) = w(c, v) = w(s, v) + w(t, v)

. 设最小割cut=INF, 任选一个点s到集合A中, 定义W(A, p)为A中的所有点到A外一点p的权值总和.

. 对刚才选定的s, 更新W(A,p)(该值递增).

. 选出A外一点p, 且W(A,p)最大的作为新的s, 若A!=|V|, 则继续2. //最大割

4. 把最后进入A的两点记为s和t, 用W(A,t)更新cut.

5. 合并st，即新建顶点u, 边权w(u, v)=w(s, v)+w(t, v), 删除顶点s和t, 以及与它们相连的边

. 若|V|!=1则继续1.

Stoer−Wagner的正确性： 
设S和T是图G的2个顶点，图G的全局最小割要么是S−T的最小割，此时S和T在G的全局最小割的2个不同的子集中，要么就是G中将S和T合并得的的新图G′的全局最小割，此时S和T在G的全局最小割的同一子集中。

合并后对边权进行调整对全局最小割没有任何影响。所以只需要不断求出当前图中任意2个点的最小割，然后合并这2个点。不断缩小图的规模求得最小割。

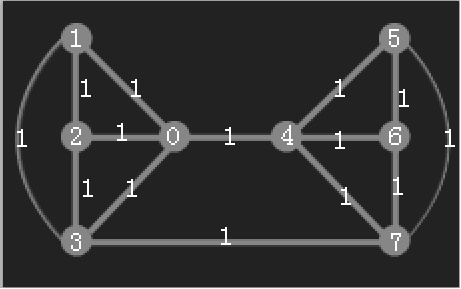       5,6合并成        

 #include <cstdio>
 #include <cstring>
 #include <algorithm>

 using namespace std;

 int e[][]; //边权
 int w[];      //各点与A集合中所有点的边权之和, w(A,x)=∑w(id[i],x) id[i]∈A
 int id[];     //顶点的重新索引，由于合并顶点的需要
 bool vis[];   //顶点是否已访问

 int main()
 {
     int n,m;
     while(scanf("%d%d",&n,&m)!=EOF)
     {
         memset(e,, sizeof(e));
         for(int i=;i<n;i++)id[i]=i;//未合并之前，各顶点索引自己
         for(int i=;i<m;i++)
         {
             int u,v,c;
             scanf("%d%d%d",&u,&v,&c);
             e[u][v]+=c;
             e[v][u]+=c;//无向图
         }

         int ans=0x3f3f3f3f;//全局最小割
         while(n>)
         {
             memset(vis,, sizeof(vis));
             memset(w,, sizeof(w));
             int s,t=;//最后两个顶点
             vis[]=;//默认第一个顶点入集合A
             for(int i=;i<n;i++)
             {
                 s=t;
                 t=-;
                 for(int j=;j<n;j++)
                 {
                     if(!vis[j])
                     {
                         w[j]+=e[id[j]][id[s]];
                         if(t==-||w[j]>w[t])t=j;//找最大的割集
                     }
                 }
                 vis[t]=; //加入集合A
             }
             ans=min(ans,w[t]);
             for(int i=;i<n;i++)  // 合并s,t为s点
             {
                 if(i==s||i==t)continue;
                 e[id[i]][id[s]]+=e[id[i]][id[t]];
                 e[id[s]][id[i]]+=e[id[i]][id[t]]; //边权w(s, v)=w(s, v)+w(t, v)
             }
             id[t]=id[--n]; // 赋值顶点n-1从而删除t点, 顶点数量-1
         }
         printf("%d\n",ans);
     }
     return ;
 }

参考自：http://www.hankcs.com，yogykwan和QAQqwe